二分查找法
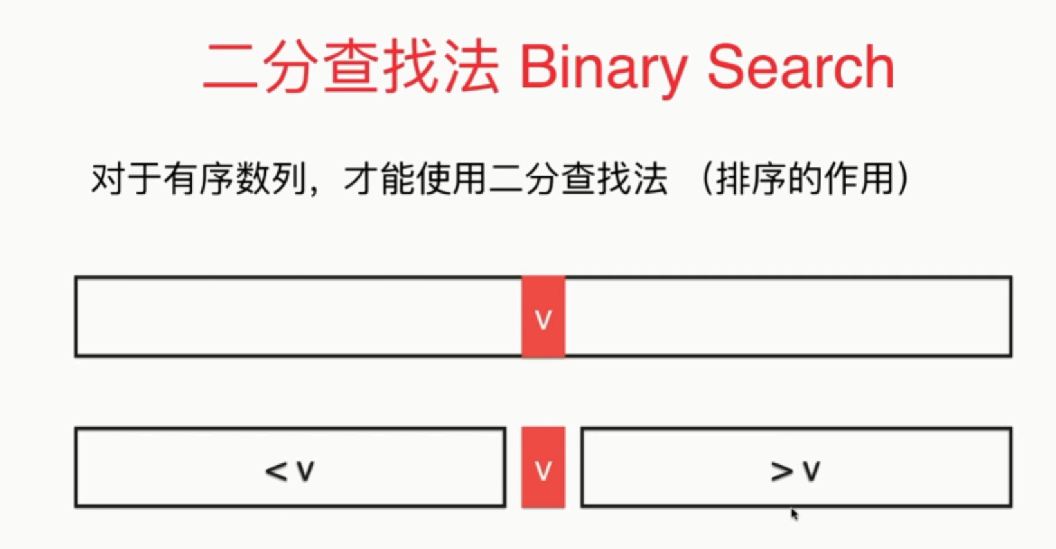
二分搜索:在一个有序的数组中将数组一分为二,根据中点值与目标值的大小缩小查找区域,递归该过程。
1 // 二分查找法,在有序数组arr中,查找target 2 // 如果找到target,返回相应的索引index 3 // 如果没有找到target,返回-1 4 template<typename T> 5 int binarySearch(T arr[], int n, T target) { 6 // 在arr[l...r]之中查找target 7 int l = 0, r = n - 1; 8 while (l <= r) { 9 10 //int mid = (l + r)/2; 11 int mid = l + (r - l) / 2; 12 if (arr[mid] == target) 13 return mid; 14 15 if (arr[mid] > target) 16 r = mid - 1; 17 else 18 l = mid + 1; 19 } 20 21 return -1; 22 } 23 template<typename T> 24 int __binarySearch2(T arr[], int l, int r, T target) { 25 if (l > r) 26 return -1; 27 28 int mid = (l + r) / 2; 29 if (arr[mid] == target) 30 return mid; 31 else if (arr[mid] > target) 32 return __binarySearch2(arr, 0, mid - 1, target); 33 else 34 return __binarySearch2(arr, mid + 1, r, target); 35 } 36 template<typename T> 37 int binarySearch2(T arr[], int n, T target) { 38 return __binarySearch2(arr, 0, n - 1, target); 39 }
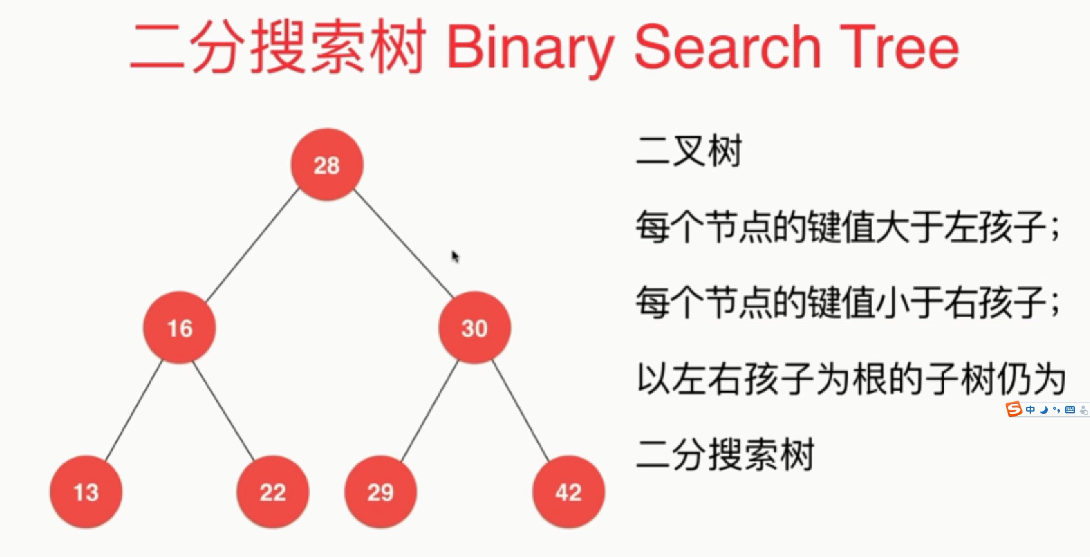
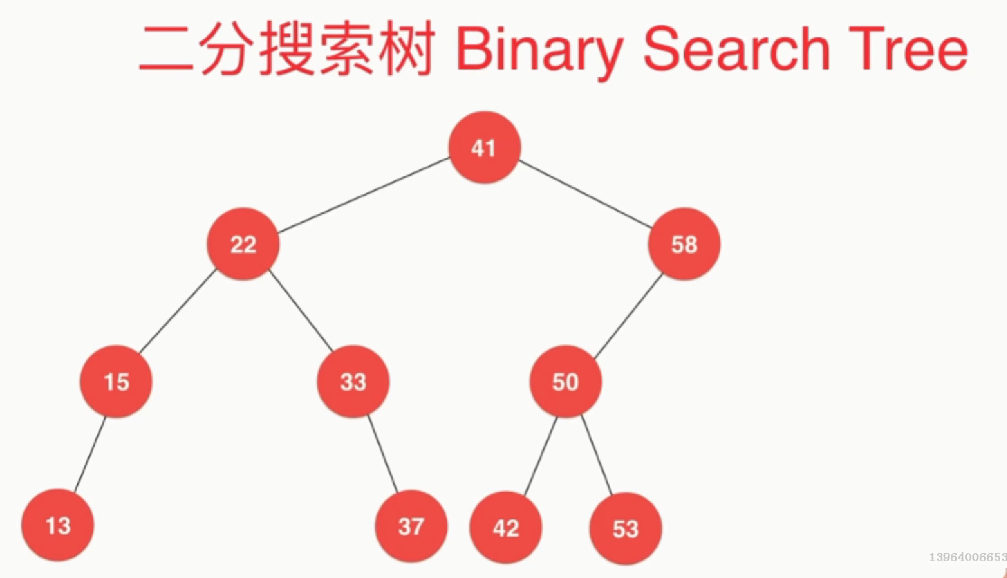
二分搜索树:每个节点的左孩子小于根节点,每个节点的右孩子大于根节点
1 //二叉搜索树,包括左孩子和右孩子,键合值 2 template<typename Key, typename Value> 3 class BST { 4 private: 5 struct Node { 6 Key key; 7 Value value; 8 Node *left; 9 Node * right; 10 Node(Key key, Value value) { 11 this->key = key; 12 this->value = value; 13 this->left = this->right = NULL; 14 } 15 Node(Node *node) { 16 this->key = node->key; 17 this->value = node->value; 18 this->left = node->left; 19 this->right = node->right; 20 } 21 }; 22 Node *root; 23 int count; 24 public: 25 BST(){ 26 root = NULL; 27 count = 0; 28 } 29 ~BST() { 30 destroy(root); 31 } 32 int size() { return count; } 33 bool isEmpty() { 34 return count == 0; 35 } 36 void insert(Key key, Value value) { 37 root = insert(root, key, value); 38 } 39 bool contain(Key key) { 40 return contain(root, key); 41 } 42 Value* search(Key key) { 43 return search(root, key); 44 } 45 // 前序遍历 46 void preOrder() { 47 preOrder(root); 48 } 49 50 // 中序遍历 51 void inOrder() { 52 inOrder(root); 53 } 54 55 // 后序遍历 56 void postOrder() { 57 postOrder(root); 58 } 59 // 层序遍历 60 void levelOrder() { 61 62 queue<Node*> q; 63 q.push(root); 64 while (!q.empty()) { 65 66 Node *node = q.front(); 67 q.pop(); 68 69 cout << node->key << endl; 70 71 if (node->left) 72 q.push(node->left); 73 if (node->right) 74 q.push(node->right); 75 } 76 } 77 // 寻找最小的键值 78 Key minimum() { 79 assert(count != 0); 80 Node* minNode = minimum(root); 81 return minNode->key; 82 } 83 84 // 寻找最大的键值 85 Key maximum() { 86 assert(count != 0); 87 Node* maxNode = maximum(root); 88 return maxNode->key; 89 } 90 91 // 从二叉树中删除最小值所在节点 92 void removeMin() { 93 if (root) 94 root = removeMin(root); 95 } 96 97 // 从二叉树中删除最大值所在节点 98 void removeMax() { 99 if (root) 100 root = removeMax(root); 101 } 102 // 从二叉树中删除键值为key的节点 103 void remove(Key key) { 104 root = remove(root, key); 105 } 106 private: 107 // 向以node为根的二叉搜索树中,插入节点(key, value) 108 // 返回插入新节点后的二叉搜索树的根 109 Node* insert(Node* node, Key key, Value value) { 110 if (node == NULL){ 111 count++; 112 return new Node(key, value); 113 } 114 if (key == node->key) { 115 node->value = value; 116 } 117 else if (key < node->key) 118 node->left = insert(node->left, key, value); 119 else // key > node->key 120 node->right = insert(node->right, key, value); 121 return node; 122 } 123 // 查看以node为根的二叉搜索树中是否包含键值为key的节点 124 bool contain(Node* node, Key key) { 125 126 if (node == NULL) 127 return false; 128 129 if (key == node->key) 130 return true; 131 else if (key < node->key) 132 return contain(node->left, key); 133 else // key > node->key 134 return contain(node->right, key); 135 } 136 137 // 在以node为根的二叉搜索树中查找key所对应的value 138 Value* search(Node * node, Key key) { 139 if (node == NULL) { 140 return NULL; 141 } 142 if (key == node->key) { 143 return &(node->value); 144 } 145 else if (key < node->key) { 146 return search(node->left, key); 147 } 148 else { 149 return search(node->right, key); 150 } 151 } 152 void preOrder(Node * node) { 153 if (node != NULL) { 154 cout << node->key << endl; 155 preOrder(node->left); 156 preOrder(node->right); 157 } 158 } 159 void inOrder(Node * node) { 160 if (node != NULL) { 161 preOrder(node->left); 162 cout << node->key << endl; 163 preOrder(node->right); 164 } 165 } 166 void postOrder(Node * node) { 167 if (node != NULL) { 168 preOrder(node->left); 169 preOrder(node->right); 170 cout << node->key << endl; 171 } 172 } 173 void destroy(Node* node) { 174 175 if (node != NULL) { 176 destroy(node->left); 177 destroy(node->right); 178 delete node; 179 count--; 180 } 181 } 182 Node* minmum(Node *node) { 183 if (node->left == NULL) { 184 return node; 185 } 186 minmum(node->left); 187 } 188 // 在以node为根的二叉搜索树中,返回最大键值的节点 189 Node* maximum(Node* node) { 190 if (node->right == NULL) 191 return node; 192 193 return maximum(node->right); 194 } 195 Node* removeMin(Node *node) { 196 if (node->left == NULL) { 197 198 Node* rightNode = node->right; 199 delete node; 200 count--; 201 return rightNode; 202 } 203 204 node->left = removeMin(node->left); 205 return node; 206 } 207 Node* removeMax(Node *node) { 208 if (node->right == NULL) { 209 210 Node* leftNode = node->left; 211 delete node; 212 count--; 213 return leftNode; 214 } 215 node->right = removeMin(node->right); 216 return node; 217 } 218 Node* remove(Node *node, Key key) { 219 if (node == NULL) { 220 return NULL; 221 } 222 if (node->key == key) { 223 if (node->left == NULL) {//要删除节点左节点为0也就是最小值节点 224 Node *rightNode = node->right; 225 delete node; 226 count--; 227 return rightNode; 228 } 229 if (node->right== NULL) {//要删除节点左节点为0也就是最小值节点 230 Node *leftNode = node->left; 231 delete node; 232 count--; 233 return leftNode; 234 } 235 Node *successor = new Node(minmum(node->right));//找到后继节点 236 count++; 237 successor->right = removeMin(node->right);//删除后继位置元素,将其放到合适的位置 238 successor->left = node->left; 239 delete node; 240 count--; 241 return successor; 242 } 243 else if (key < node->key) { 244 node->left = remove(node->left, key); 245 return node; 246 } 247 else { 248 node->right = remove(node->right, key); 249 return node; 250 } 251 252 remove(node, key); 253 } 254 };
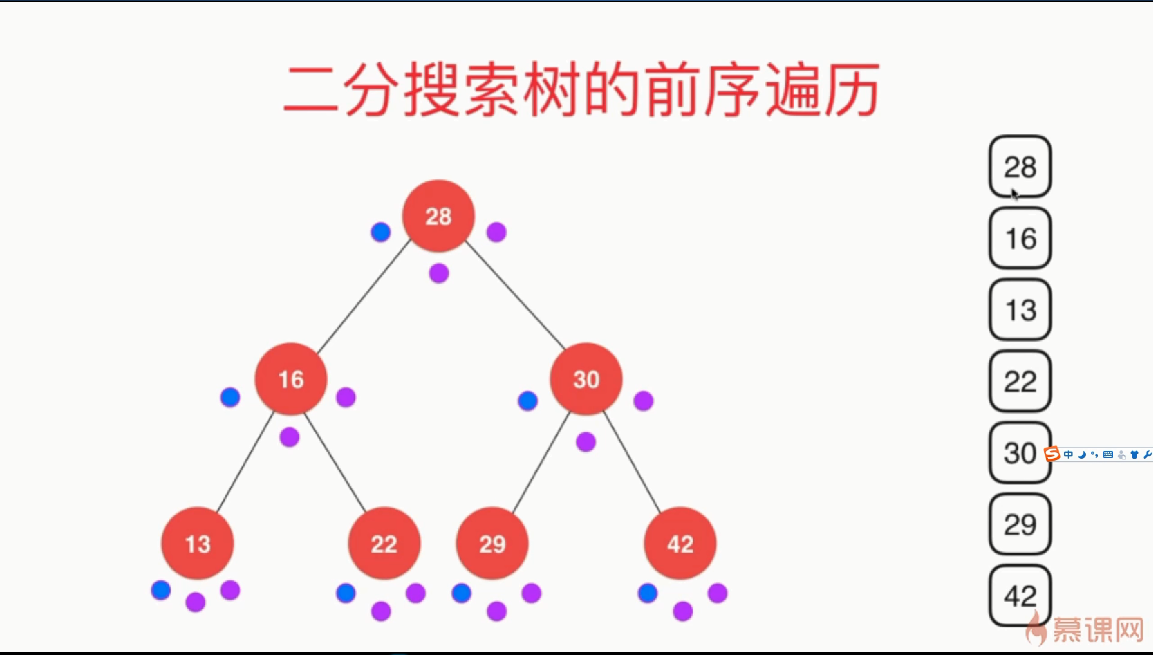


1 void preOrder(Node * node) { 2 if (node != NULL) { 3 cout << node->key << endl; 4 preOrder(node->left); 5 preOrder(node->right); 6 } 7 } 8 void inOrder(Node * node) { 9 if (node != NULL) { 10 preOrder(node->left); 11 cout << node->key << endl; 12 preOrder(node->right); 13 } 14 } 15 void postOrder(Node * node) { 16 if (node != NULL) { 17 preOrder(node->left); 18 preOrder(node->right); 19 cout << node->key << endl; 20 } 21 }



