堆排序
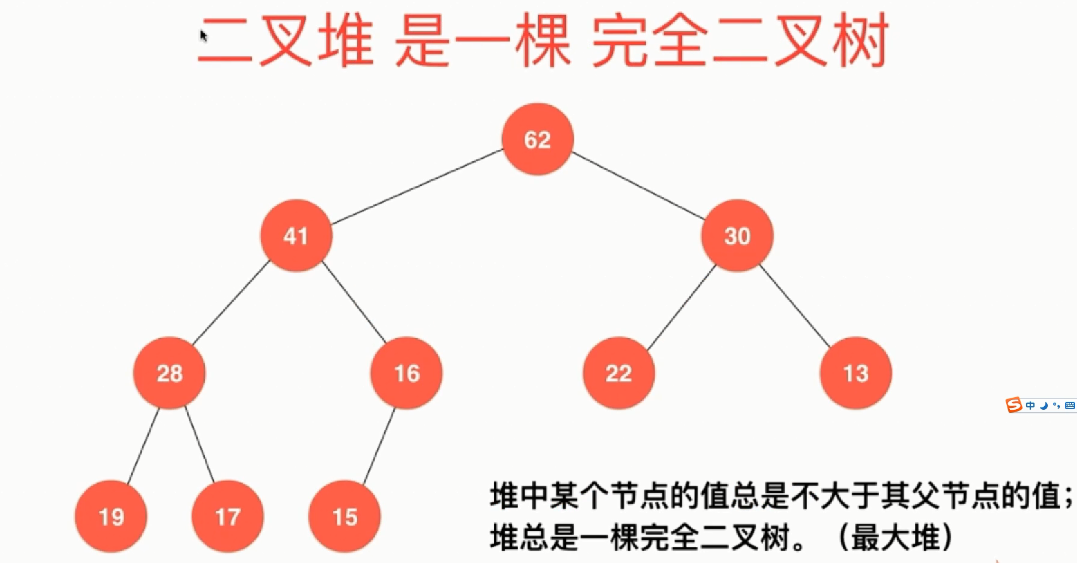
堆是一种数据结构,最大堆性质:堆中的节点值总是不大于其父节点的值,堆是一颗完全二叉树。
1 template<typename Item> 2 class MaxHeap { 3 private: 4 Item *data; 5 int count; 6 int capacity; 7 void shiftUp(int k) {//将新加入的元素与父节点依次比较,使之满足最大堆 8 while (k>1 && data[k / 2] < data[k]) { 9 swap(data[k / 2], data[k]); 10 k /=2; 11 } 12 } 13 void shiftDown(int k) { 14 while (2 * k <= count) { 15 int j = 2 * k; //在此轮循环中, data[k]和data[j]交换位置 16 if (j + 1 <= count&&data[j] < data[j + 1]) 17 j++; 18 // data[j] 是 data[2*k]和data[2*k+1]中的最大值 19 if (data[k] >= data[j]) 20 break; 21 swap(data[k], data[j]); 22 k = j;//下一层 23 } 24 }
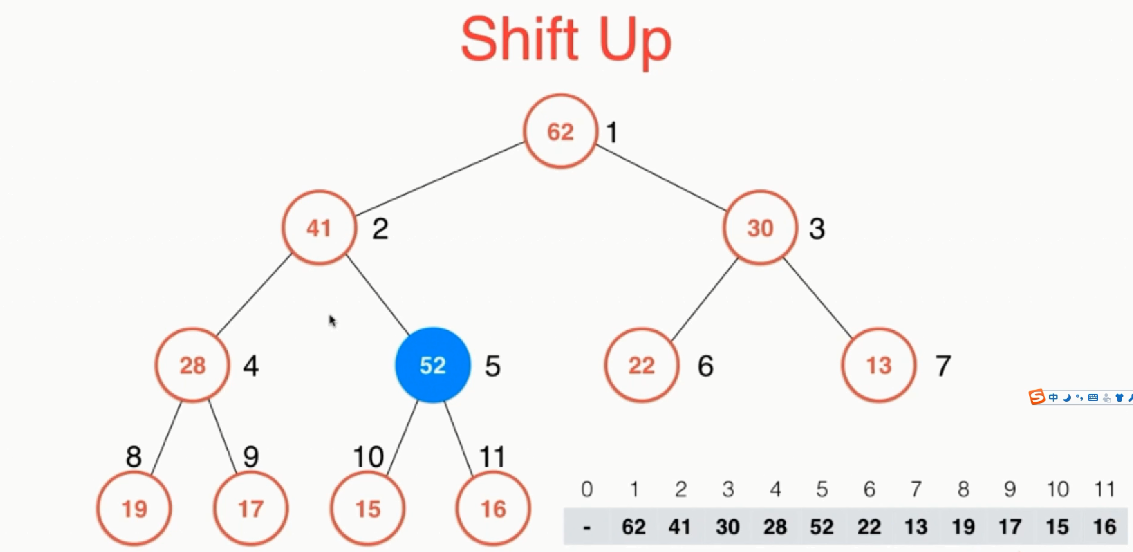

26 public: 27 MaxHeap(int capacity) { 28 data = new Item[capacity + 1];//开辟的空间容量 29 count = 0;//表示的是堆中的元素数目 30 this->capacity = capacity; 31 } 32 MaxHeap(Item arr[], int n) { 33 data = new Item[n + 1]; 34 capacity = n; 35 36 for (int i = 0; i < n; i++) 37 data[i + 1] = arr[i]; 38 count = n; 39 40 for (int i = count / 2; i >= 1; i--) 41 shiftDown(i); 42 } 43 ~MaxHeap() { 44 delete[] data; 45 } 46 int size() { 47 return count; 48 } 49 bool isEmpty() { 50 return count == 0; 51 } 52 void insert(Item item) { 53 assert(count + 1 <= capacity); 54 data[count + 1] = item; 55 shiftUp(count + 1); 56 count++; 57 } 58 Item extractMax() { 59 assert(count > 0); 60 Item ret = data[1]; 61 swap(data[count], data[1]); 62 count--; 63 shiftDown(1); 64 65 return ret; 66 } 67 Item getMax() { 68 assert(count > 0); 69 return data[1]; 70 } 71 };
堆排序:利用堆将数组进行排序,堆中的根节点存储的是最大值,由此将队中的值先插入操作,再进行去除最大值放到排序数组中,heapify过程。
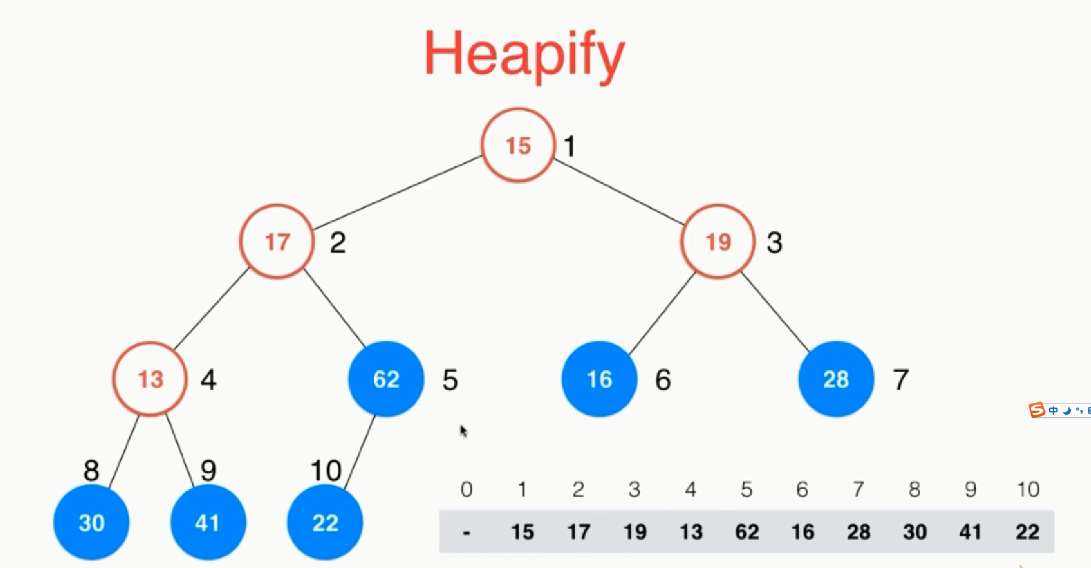
1 template<typename T> 2 void heapSort2(T arr[], int n) { 3 4 MaxHeap<T> maxheap = MaxHeap<T>(arr, n); 5 for (int i = n - 1; i >= 0; i--) 6 arr[i] = maxheap.extractMax(); 7 8 } 9 10 11 template<typename T> 12 void heapSort1(T arr[], int n) { 13 14 MaxHeap<T> maxheap = MaxHeap<T>(n);//构造一个最大堆 15 for (int i = 0; i < n; i++) 16 maxheap.insert(arr[i]);//将数组中的元素插入堆中 17 18 for (int i = n - 1; i >= 0; i--) 19 arr[i] = maxheap.extractMax();//将堆中元素倒序插入到数组中 20 21 } 22 //原地堆排序 23 using namespace std; 24 template<typename T> 25 void __shiftDown(T arr[], int n, int k) { 26 while (2 * k + 1 < n) { 27 int j = 2 * k + 1; 28 if (j + 1 < n&&arr[j + 1] > arr[j]) { 29 j = j + 1; 30 } 31 if (arr[k] >= arr[j]) break; 32 swap(arr[k], arr[j]); 33 k = j; 34 } 35 } 36 template <typename T> 37 void heapSort(T arr[], int n) { 38 for (int i = (n - 1) / 2; i >= 0; i--)//进行heapify操作将数组转换成堆的样子 39 __shiftDown(arr, n, i);//找到每个非叶子节点进行shiftDown; 40 for (int i = n - 1; i > 0; i--) { 41 swap(arr[0], arr[i]);//将最大的元素换到数组的最后未排序部分 42 __shiftDown(arr, i, 0);//进行shiftDown维护堆 43 } 44 }
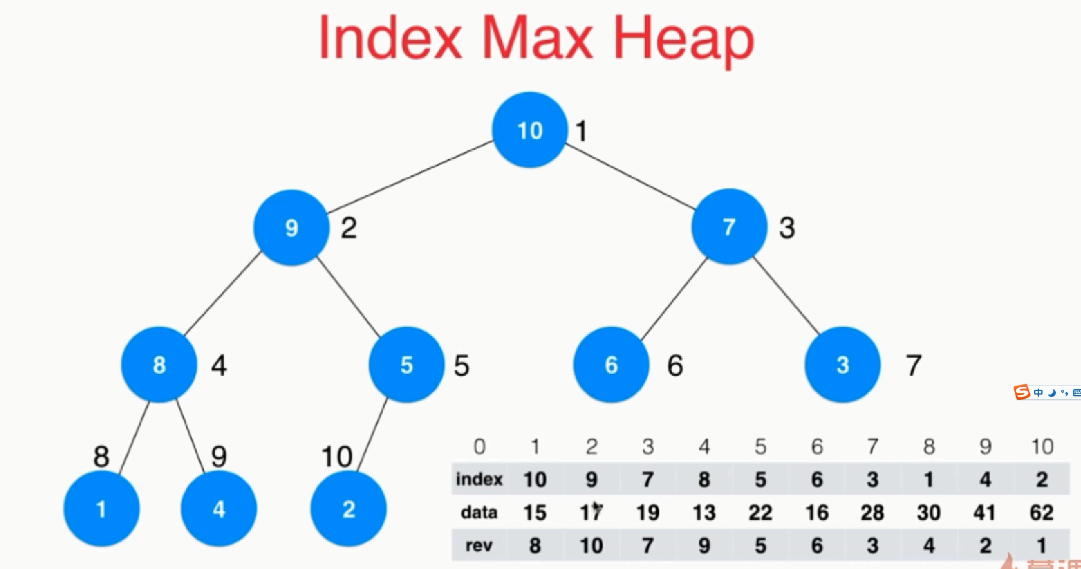
最大索引堆:堆中存储的元素是数组的索引
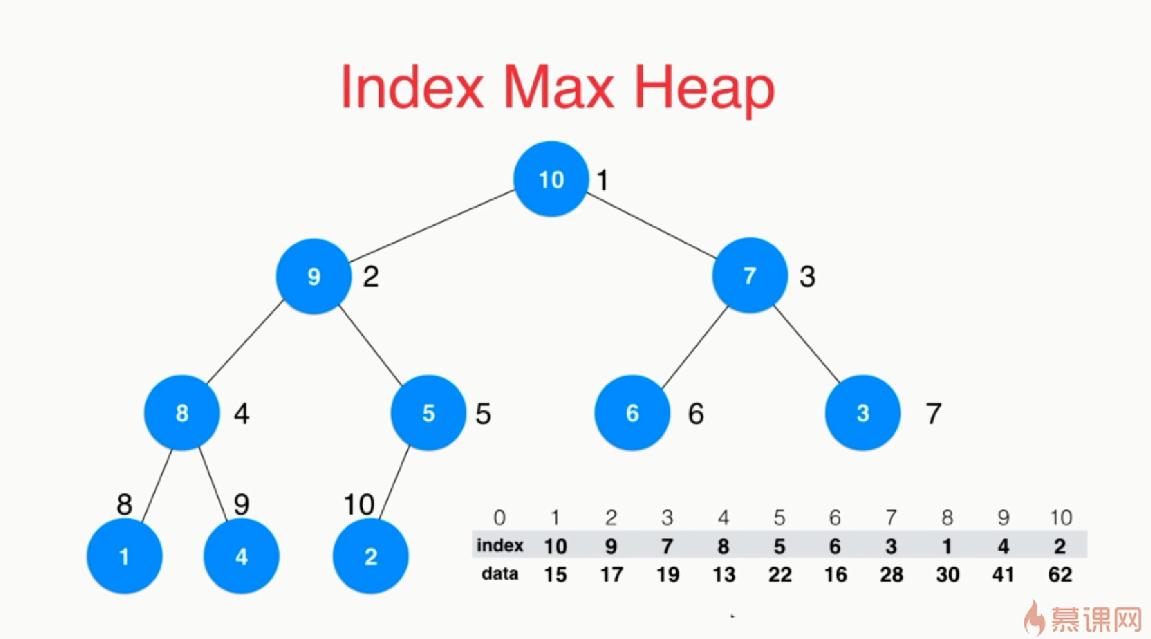
1 template<typename Item> 2 class IndexMaxHeap { 3 private: 4 Item *data; 5 int *indexes; 6 int *reverse; 7 int count; 8 int capacity; 9 10 11 void shiftUp(int k) {//交换索引 12 while (k>1 && data[indexes[k / 2]] < data[indexes[k]]) { 13 swap(indexes[k / 2], indexes[k]); 14 reverse[indexes[k / 2]] = k / 2; 15 reverse[indexes[k]] = k; 16 k /= 2; 17 } 18 } 19 void shiftDown(int k) { 20 while (2 * k <= count) { 21 int j = 2 * k; //在此轮循环中, data[k]和data[j]交换位置 22 if (j + 1 <= count&&data[indexes[j]] < data[indexes[j] + 1]) 23 j++; 24 // data[j] 是 data[2*k]和data[2*k+1]中的最大值 25 if (data[indexes[k]] >= data[indexes[j]]) 26 break; 27 swap(indexes[k], indexes[j]); 28 reverse[indexes[k]] = k ; 29 reverse[indexes[j]] = j; 30 k = j;//下一层 31 } 32 33 } 34 public: 35 IndexMaxHeap(int capacity) { 36 data = new Item[capacity + 1];//开辟的空间容量 37 indexes = new int[capacity + 1];//为索引开辟空间 38 reverse = new int[capacity + 1]; 39 for (int i = 0; i <= capacity; i++) 40 reverse[i] = 0; 41 count = 0;//表示的是堆中的元素数目 42 this->capacity = capacity; 43 } 44 45 ~IndexMaxHeap() { 46 delete[] data; 47 delete[] indexes; 48 delete[] reverse; 49 } 50 int size() { 51 return count; 52 } 53 bool isEmpty() { 54 return count == 0; 55 } 56 void insert(int i,Item item) { 57 assert(i + 1 >= 1 && i + 1 < capacity); 58 assert(count + 1 <= capacity); 59 i += 1; 60 indexes[count + 1] = i; 61 reverse[count + 1] = i; 62 data[i] = item; 63 count++; 64 shiftUp( count ); 65 66 } 67 Item extractMax() { 68 assert(count > 0); 69 Item ret = data[indexes[1]]; 70 swap(indexes[1], indexes[count]); 71 reverse[indexes[count]] = 0; 72 reverse[indexes[1]] = 1; 73 count--; 74 shiftDown(1); 75 76 return ret; 77 } 78 // 传入的i对用户而言,是从0索引的 79 int extractMaxIndex() { 80 assert(count > 0); 81 int ret = indexes[1]-1; 82 swap(indexes[1], indexes[count]); 83 reverse[indexes[count]] = 0; 84 reverse[indexes[1]] = 1; 85 count--; 86 shiftDown(1); 87 88 return ret; 89 } 90 Item getMax(int i) { 91 assert(count > 0); 92 return data[indexes[1]]; 93 } 94 int getMaxIndex() { 95 assert(count > 0); 96 return indexes[1] - 1; 97 } 98 bool contain(int i) { 99 assert(i + 1 >= 1 && i + 1 <= capacity); 100 return reverse[i + 1] != 0; 101 } 102 103 Item getItem(int i) { 104 assert(contain(i)); 105 return data[i + 1]; 106 } 107 108 void change(int i, Item newItem) { 109 110 assert(contain(i)); 111 i += 1; 112 data[i] = newItem; 113
114 // 找到indexes[j] = i, j表示data[i]在堆中的位置 115 // 之后shiftUp(j), 再shiftDown(j) 116 117 // for( int j = 1 ; j <= count ; j ++ ) 118 // if( indexes[j] == i ){ 119 // shiftUp(j); 120 // shiftDown(j); 121 // return; 122 // } 123 124 int j = reverse[i]; 125 shiftUp(j); 126 shiftDown(j); 127 } 128 // test reverse index 129 bool testReverseIndex() { 130 131 int *copyIndexes = new int[count + 1]; 132 int *copyReverseIndexes = new int[count + 1]; 133 134 for (int i = 0; i <= count; i++) { 135 copyIndexes[i] = indexes[i]; 136 copyReverseIndexes[i] = reverse[i]; 137 } 138 139 copyIndexes[0] = copyReverseIndexes[0] = 0; 140 std::sort(copyIndexes, copyIndexes + count + 1); 141 std::sort(copyReverseIndexes, copyReverseIndexes + count + 1); 142 143 bool res = true; 144 for (int i = 1; i <= count; i++) 145 if (copyIndexes[i - 1] + 1 != copyIndexes[i] || copyReverseIndexes[i - 1] + 1 != copyReverseIndexes[i]) 146 res = res || false; 147 148 delete[] copyIndexes; 149 delete[] copyReverseIndexes; 150 151 if (!res) { 152 cout << "Error 1" << endl; 153 return res; 154 } 155 156 for (int i = 1; i <= count; i++) 157 if (reverse[indexes[i]] != i) { 158 cout << "Error 2" << endl; 159 return false; 160 } 161 162 return true; 163 } 164 };



