8.22 [CSP-S 2021] 交通规划 题解

本题出处为 CSP-S 2021 T4，具有相当的水准与价值。

本篇题解部分借鉴于 Alex_Wei，在此鸣谢；没有他的博客，我现在就不可能会最短路求最小割

题意较清晰，为求一张网格图的最小割变式。

当 \(k = 2\) 时，弱化为经典“狼抓兔子”，平面图最小割转对偶图最短路。对偶图的每条边设与其对偶边权值相等，两关键点之间的最短路即为所求。

下图给出了一个例子，其中所有的点都被划分为红色和黄色（将两射线分别看成源点和汇点），青色的边即为两端颜色不一的边。可以看到，转化为对偶图之后，原平面图的最小割就是转化后对偶图的最短路。

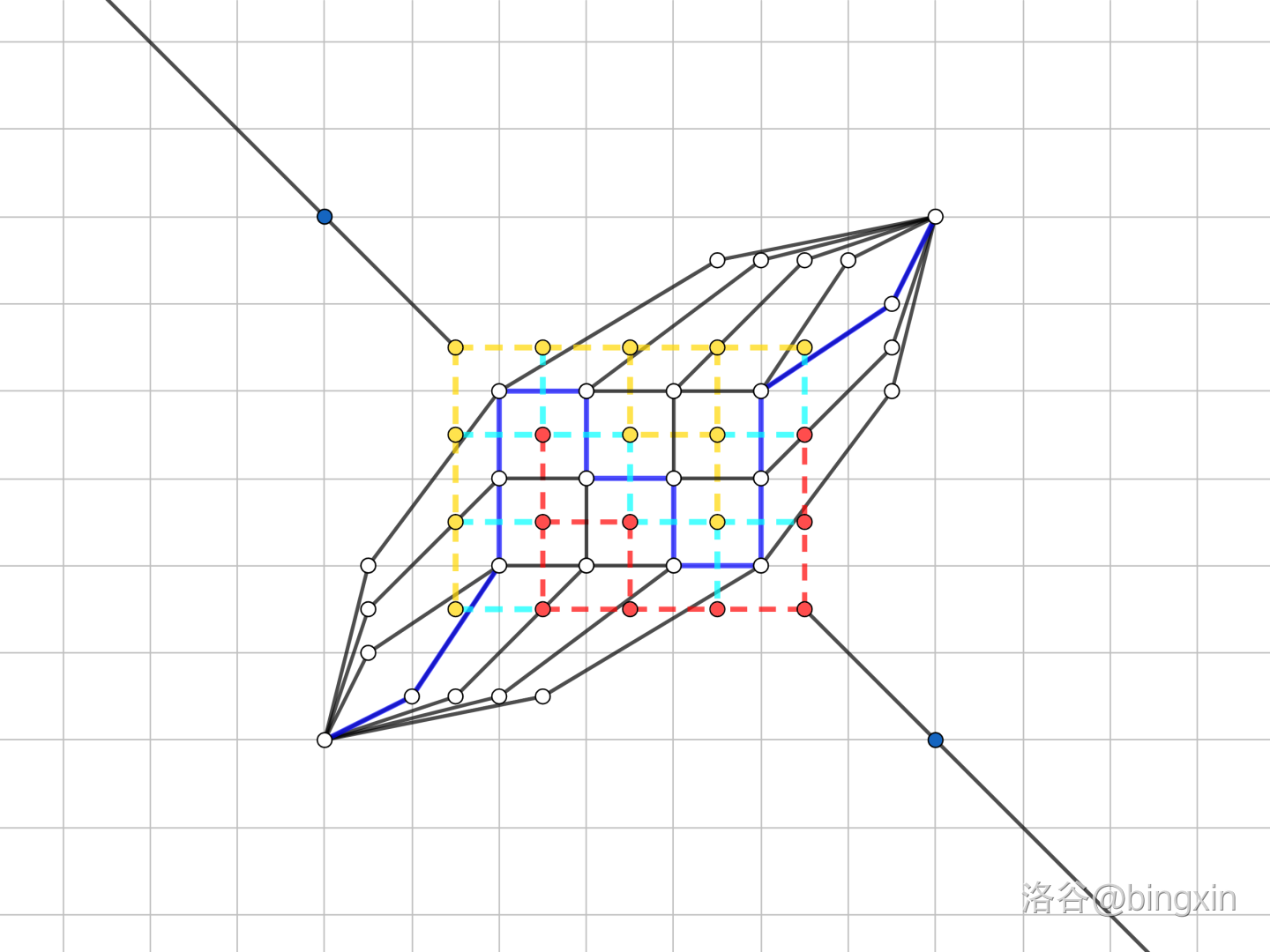
当 \(k > 2\) 时，网格图之外的关键点数量增多了，原问题得到强化，类似于 \(k = 2\) 时的做法，假设我们现在已经完成对偶图的转化，原本的的网格外面会多出 \(k\) 个关键点，每个关键点两侧有两条射线。设 \(L_i\) 为第 \(i\) 个点逆时针方向的射线颜色，\(R_i\) 同理为顺时针方向。

可以先对这 \(k\) 个点进行精简，注意到，当 \(L_i = R_i\) 时，可贪心地直接忽略这个点，因为它两边的射线颜色一致，没有必要在中间进行划分，这只会让答案不优。

这样操作之后，余下的点的 \((L_i, R_i)\) 一定是 \((0, 1)\) 和 \((1, 0)\) 交替出现的一个环，我们在两两点之间连线，路径经过的所有边颜色不同，这样，每一种匹配方案就都对应一种划分方案。

在匹配过程中，注意到性质：最优划分中任意两点的匹配不会相交。考虑这样有六个点的环，有如下相交与不相交两种情况，把中间这个结去掉，答案一定不会更劣。

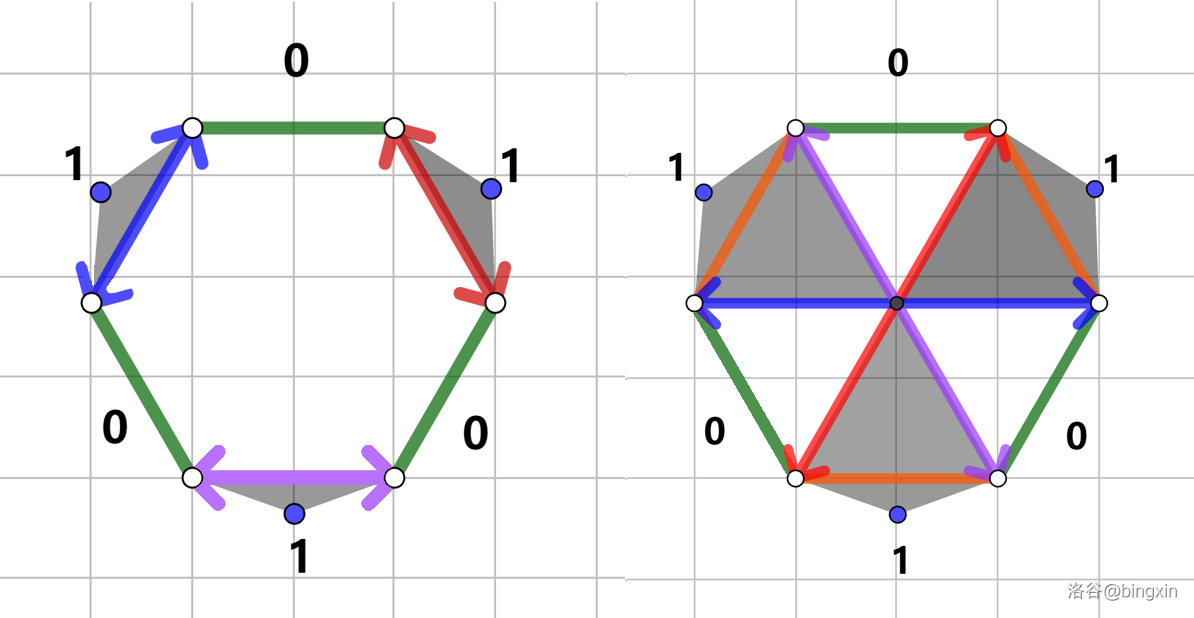
最后我们就能类似于括号匹配那样区间 DP。这个转化和 [春季测试 2023] 圣诞树 有异曲同工之妙啊（赞赏），都是得出连线不会相交的性质然后区间 DP。

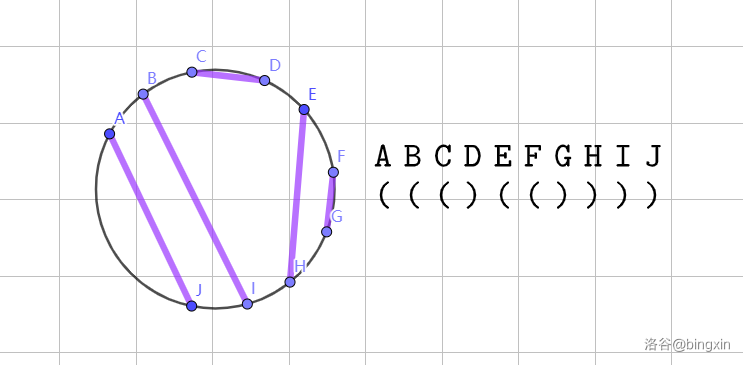
本题码量较大，实现有很多细节。

#include <bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;

constexpr int N = 3e5 + 5, S = 2e3 + 5, K = 1e2 + 5, INF = 0x3f3f3f3f;
int n, m, T;
int hed[N], nxt[N << 2], rch[N << 2], val[N << 2], idx;
void link(int u, int v, int w)
{
    nxt[++idx] = hed[u], hed[u] = idx, rch[idx] = v, val[idx] = w;
    nxt[++idx] = hed[v], hed[v] = idx, rch[idx] = u, val[idx] = w;
}

int ori, poi[N];
int trs(int i, int j) { return (m + 1) * i + j; }
void input() // 读入部分，将整张图转化为对偶图
{
    cin >> n >> m >> T;
    for (int i = 1, w, p; i < n; i++)
        for (int j = 1; j <= m; j++)
            p = trs(i, j - 1), cin >> w, link(p, p + 1, w);
    for (int i = 1, w, p; i <= n; i++)
        for (int j = 1; j < m; j++)
            p = trs(i - 1, j), cin >> w, link(p, p + m + 1, w);
    for (int i = 1; i <= (n + m) << 1; i++)
        if (i <= m)
            poi[i] = trs(0, i - 1);
        else if (i <= m + n)
            poi[i] = trs(i - m - 1, m);
        else if (i <= 2 * m + n)
            poi[i] = trs(n, 2 * m + n + 1 - i);
        else
            poi[i] = trs(2 * m + 2 * n + 1 - i, 0);
    ori = idx; // 记录原图（没有任何附加点时的边数），方便还原
}
int dis[N];
void dijkstra(const vector<int> &outer)
{
    memset(dis, 0x3f, sizeof(dis));
    priority_queue<pii, vector<pii>, greater<>> q;
    for (int u : outer)
        q.emplace(dis[u] = 0, u);
    while (!q.empty())
    {
        int pre = q.top().first, u = q.top().second;
        q.pop();
        if (pre != dis[u])
            continue;
        for (int e = hed[u]; e; e = nxt[e])
        {
            int v = rch[e], cur = pre + val[e];
            if (dis[v] > cur)
                q.emplace(dis[v] = cur, v);
        }
    }
}
int col[S], cst[S], k;
int w[K][K], f[K][K];
void solve()
{
    // 清空上一次的询问
    for (int i = 0; i < (n + 1) * (m + 1); i++)
        while (hed[i] > ori)
            hed[i] = nxt[hed[i]];
    idx = ori;

    memset(col, -1, sizeof(col)), memset(cst, 0, sizeof(cst)), cin >> k;
    for (int i = 1, w, p, c; i <= k; i++)
        cin >> w >> p >> c, col[p] = c, cst[p] = w;
    for (int i = 1; i <= (n + m) << 1; i++)
        if (i <= m)
            link(poi[i], poi[i] + 1, cst[i]);
        else if (i <= m + n)
            link(poi[i], poi[i] + m + 1, cst[i]);
        else if (i <= 2 * m + n)
            link(poi[i], poi[i] - 1, cst[i]);
        else
            link(poi[i], poi[i] - m - 1, cst[i]);

    vector<vector<int>> outer;
    int fir = 0, lst = 0;
    for (int i = 1; i <= (n + m) << 1; i++) // 开始转圈
    {
        if (col[i] == -1)
            continue;
        if (!fir)
            fir = i;
        else if (col[lst] != col[i])
        {
            vector<int> inner;
            for (int j = lst + 1; j <= i; j++)
                inner.emplace_back(poi[j]);
            outer.emplace_back(inner);
        }
        lst = i;
    }
    if (col[lst] != col[fir])
    {
        vector<int> inner;
        for (int i = lst + 1; i <= (n + m) << 1; i++)
            inner.emplace_back(poi[i]);
        for (int i = 1; i <= fir; i++)
            inner.emplace_back(poi[i]);
        outer.emplace_back(inner);
    }
    if (outer.empty()) // k 为 1 或全部消完，不需要代价
        return cout << "0\n", void();

    // 预处理两点之间最短路
    memset(w, 0x3f, sizeof(w)), memset(f, 0x3f, sizeof(f)), k = outer.size();
    for (int i = 0; i < k; i += 2)
    {
        dijkstra(outer[i]);
        for (int j = 0; j < k; j++)
        {
            for (int u : outer[j])
                w[i][j] = min(w[i][j], dis[u]);
            w[j][i] = w[i][j];
        }
    }

    // 区间 DP，简单的破环成链
    for (int i = 0; i < k; i++)
        for (int j = 0; j < k; j++)
            w[i + k][j] = w[i][j + k] = w[i + k][j + k] = w[i][j];
    for (int i = 1; i <= k << 1; i++)
        f[i][i - 1] = 0;
    for (int i = 2; i <= k; i++)
        for (int l = 1; l <= (k << 1) - i + 1; l++)
        {
            int r = l + i - 1;
            f[l][r] = f[l + 1][r - 1] + w[l][r];
            for (int x = l + 1; x < r; x += 2)
                f[l][r] = min(f[l][r], f[l][x] + f[x + 1][r]);
        }
    int ans = INF;
    for (int i = 0; i < k; i++)
        ans = min(ans, f[i][i + k - 1]);
    cout << ans << '\n';
}
signed main()
{
    ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    input();

    while (T--)
        solve();
    return 0;
}