8.13 模拟赛 T1 brackets 个人题解

题意：给出一个括号序列，以连续左右括号个数的形式，求合法的子串数量。

括号序列很常见，我们把左括号 \(\texttt{(}\) 看成 \(+1\)，右括号 \(\texttt{)}\) 看成 \(-1\)，这样一段合法的括号序列和一定为 \(0\)，且任意位置的前缀和 \(\ge 0\) ，对于暴力分，我们就可以把这个括号序列暴力建出来解决。再考虑整个括号序列，每次加进来的括号有多个，我们没必要一个个括号考虑，而直接以操作为单位，来降低操作次数。

为了方便，我们每次处理左右括号搭配的两个 c，称作一组。考虑贡献法来降复杂度，对于字符串，这个问题有很常见的转化，子串 = 所有前缀的所有后缀。好了，我们考虑右括号 \(\texttt{(}\) 对左括号 \(\texttt{)}\) 的贡献。

我们记录当前还有多少个左括号等待被匹配，若新的右括号数量大于总的左括号，那么右括号出现冗余，这时我们结束当前的统计即可。而当小于等于时，就产生了『匹配』，并与前面已经匹配的子串一起，构成更多的匹配，而我们主要处理的就是这个贡献怎么维护。我们将当前剩余左括号的数量改称为『深度』，进行一些更加深层的探讨。

引理：任何可以与之前已经匹配的子串一起构成更大匹配的子串，两串右括号的深度一定是相同的。

所以我们匹配成功时在当前深度加入贡献，查询时加上合法位置的贡献，就是这个子串总的贡献。

序列：( ( ) ( ) ) ( ) ···
深度： 1 2 1 2 1 0 1 0

	   ↓--1---↓↓----2-----↓    ↓------3-------↓
序列：( ( ( ) ) ( ( ( ) ) ) ) ( ( ( ( ( ) ) ) ) ) ( ( ···
深度： 1 2 3 2 1 2 3 4 3 2 1 0 1 2 3 4 5 4 3 2 1 0 1 2

然后我们考虑维护这个贡献。发现并不是所有成功匹配的位置都能对之后贡献，因为深的贡献之间会被浅的贡献截断，就像上面标注的三个子串，都在 1 深度处结束，但 1 能对 2 贡献但却不能贡献 3，我们来体现到图上。

（图片使用Clip Studio Paint（CSP）绘制，多种需求，一应俱全！）

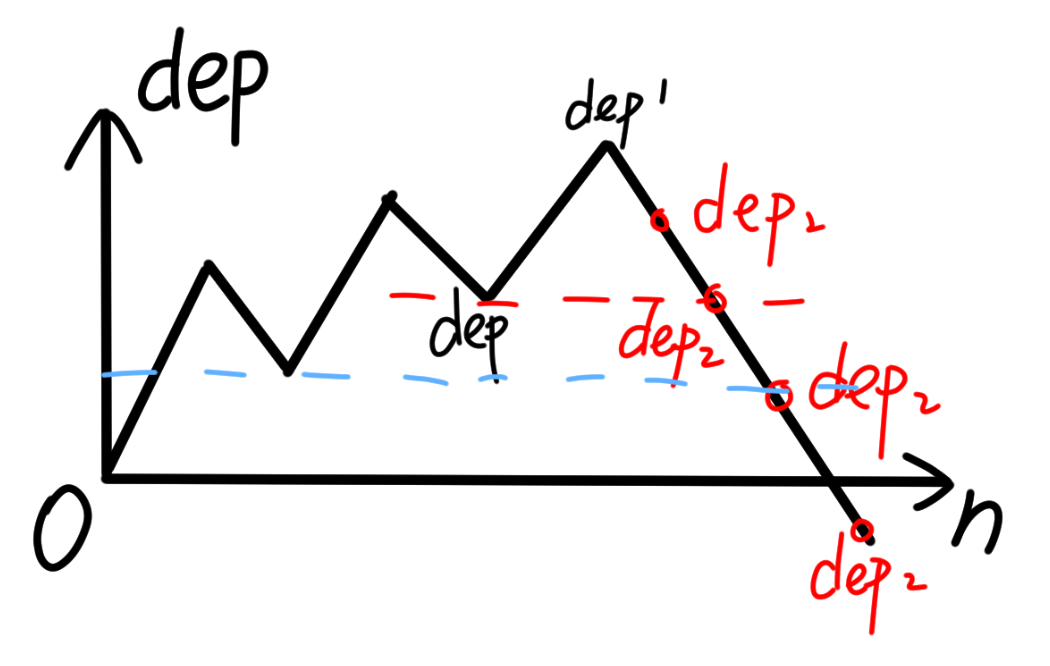
形象化来讲，我们每个操作要做的事，分为两个部分：

• 统计当前答案，这又分为两部分
  • 这一组操作本身的匹配 \(\texttt{dep1} \sim \texttt{dep2}\)
  • \(\texttt{dep} \sim \texttt{dep2}\) 之间的已经匹配的贡献
• 记录当前的贡献
  在 \(\texttt{dep2}\) 处贡献 \(+1\)，同时 \(>\texttt{dep2}\) 的贡献清零（被覆盖）。

我们来看图上红色 \(\texttt{dep2}\) 的几种可能取值。

• 当 \(\texttt{dep2} < \texttt{dep}\) 时，就是本组右括号的数量。
• 当 \(\texttt{dep2} < 0\) 时，我们结束本轮统计。
• 当 \(0 \le \texttt{dep2} \le \texttt{dep}\)，我们需要加上前面操作的贡献。

可以发现，能产生 \(\texttt{dep2}\) 到 \(\texttt{dep}\) 之间贡献的位置并不多，前面提到，每加进来一个新的贡献，都会把比他高的贡献覆盖，我们依次往前考虑每个操作，发现合法位置

\[\huge{单调不升} \]

我们用单调栈维护，每个位置维护复杂度总共均摊 \(O(1)\)，代码有一些细节要注意，最后就在 \(O(n)\) 时间内以小常数写法解决了这道题。

（不掐头不去尾30+Line，欢迎来挑战最简做法）

#include <bits/stdc++.h>
using namespace std;

constexpr int N = 1e7 + 10;
long long n, m[2], c[N], x, y, z;
stack<pair<long long, int>> tag; // 开 O2 了，我直接用的 STL

signed main()
{
    ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    cin >> n >> x >> y >> z >> m[0] >> m[1] >> c[0] >> c[1];
    for (int i = 2; i < n; i++)
        c[i] = (c[i - 1] * x + c[i - 2] * y + z) % m[i & 1] + 1;
    long long dep = 0, ans = 0; // dep < 0 is meaningless
    for (int i = 0; i < n; i += 2)
    {
        long long dep1 = dep + c[i], dep2 = dep1 - c[i + 1];
        if (dep2 < 0)
        {
            ans += dep1, dep = 0;
            while (!tag.empty())
                ans += tag.top().second, tag.pop(); // 之前的贡献都可以加入
        }
        else
        {
            ans += dep1 - dep2; // 当前组的贡献
            while (!tag.empty() && tag.top().first > dep2)
                ans += tag.top().second, tag.pop();
            if (!tag.empty() && tag.top().first == dep2)
                ans += tag.top().second, tag.top().second += 1; // 深度相同时累积
            else
                tag.emplace(dep2, 1);
            dep = dep2;
        }
    }
    cout << ans;
    return 0;
}