WQS二分学习笔记

注：本文不区分凸包与凸壳，wqs 二分也称带权二分

Part. 1 简介

wqs 二分通常用来解决下面这类问题：

给定若干 \(n\) 个物品，要求从中恰好选 \(m\) 次，最大化 / 最小化 选的物品权值和。

使用 wqs 二分解决这类题目需要一些条件，就像所有的二分需要有单调性，wqs 二分需要一个比较特殊的单调性：设 \(g(i)\) 为选 \(i\) 个物品的最优答案，函数 \(g(i)\) 的图像为一 凸包 （上下均可）。

这里利用的就是凸包斜率的 不上升 / 不下降 。（想想为什么这么说？）

然而在实际判断时也不需要真正画出来，简而言之，题目能转化成：一共有 \(n\) 个数，要求刚好选 \(m\) 次，有某种限制，以某种方式计算每次选的物品的某个属性和，选多少次以及怎么选都会影响到答案。

然后用动态规划，能设 \(dp(i,j)\) ：到 \(i\) 为止，选了 \(j\) 次的最优答案, 转移：

\[dp(i,j)=max⁡/min⁡(dp(k,j−1)+cost(k,i)) \]

之类的。

因为至少有 \(nm\) 个状态，复杂度不管怎么优化都至少是 \(O(nm)\) 及以上的，无法接受。

但打表发现（形成凸包 / 斜率单调 / 满足特点），且如果这题没有恰好个数限制 DP 可以降维转移，就可以用 \(\text{WQS二分}\) 降维。

时间复杂度通常一个 \(n\) 降成 \(\log\)，\(O(n \log V)\)。

Part. 2 算法分析

二分什么

在具体算的时候，二分一个 \(mid\) ，表示选一次物品的附加权值，所以选的次数越多，权值越大。

所以当最优方案选的物品次数大于 \(m\) 时，就减小 \(mid\) ，否则增加 \(mid\) 。

最后答案去掉 \(mid\) 的影响即可。

如何 \(\text{check}\)

我们现在已经有了 \(f(i)\) 图像构成的凸包，显然只要求出当 \(x = m\) 时的函数值即可，但这个确切的凸包现在是不知道的，我们只知道他是一个 上凸包 （放张图）

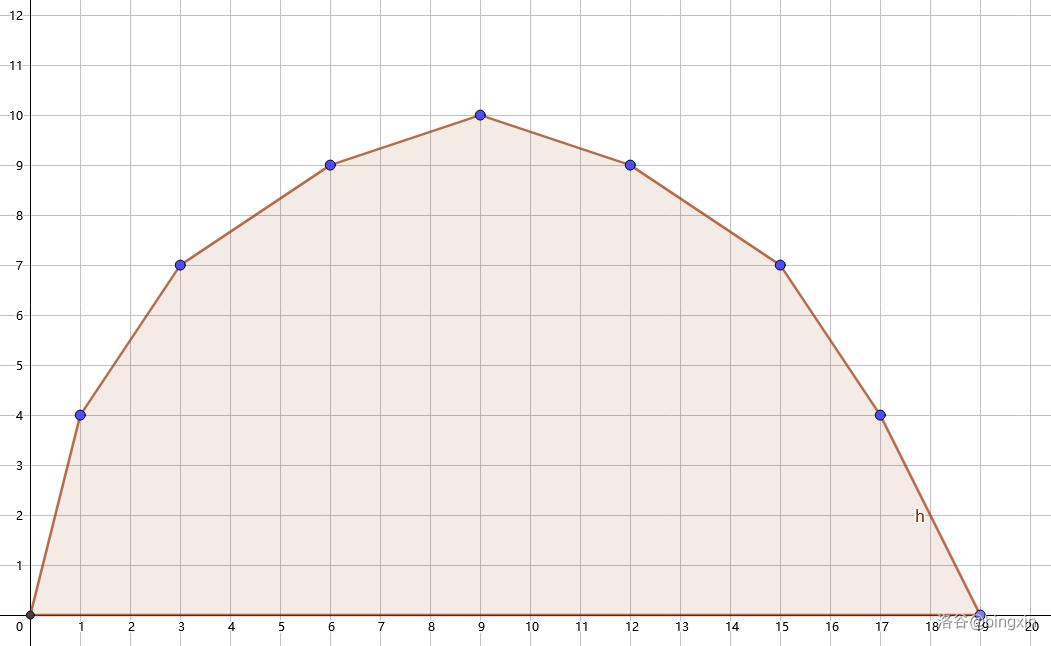
所以对于这几个点，我们可以 用直线去切凸包，来得到此时的最大值，看起来就像是这样

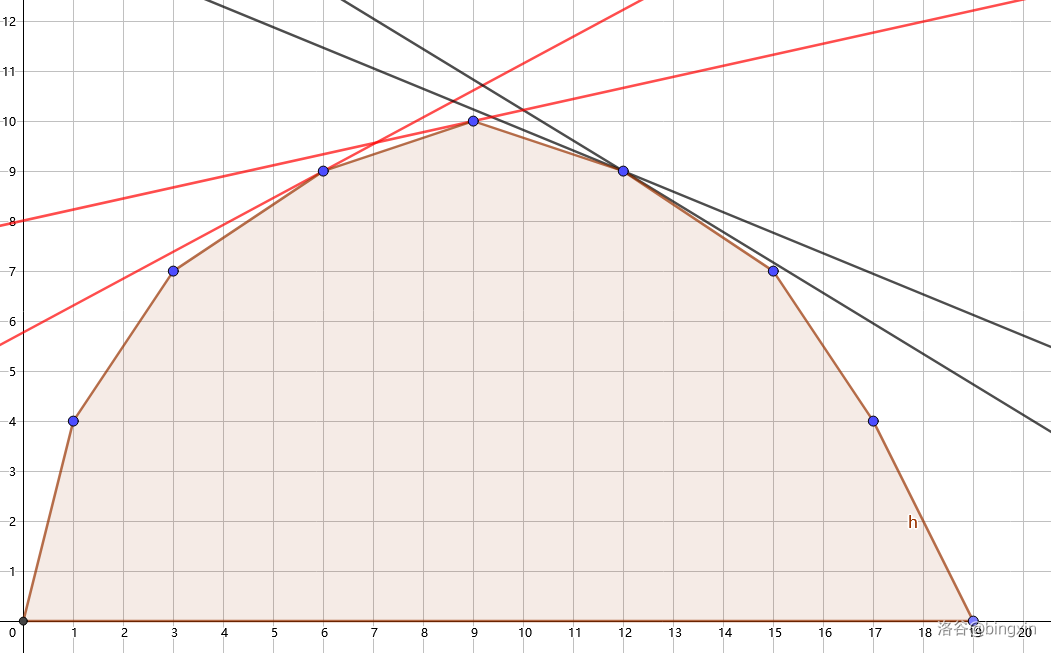
然后我们就可以由于 \(f(x)\) 的斜率单调，直线切到的点同样单调，如图，斜率越小，切到凸包的点越大。最后截距就是我们要的答案。

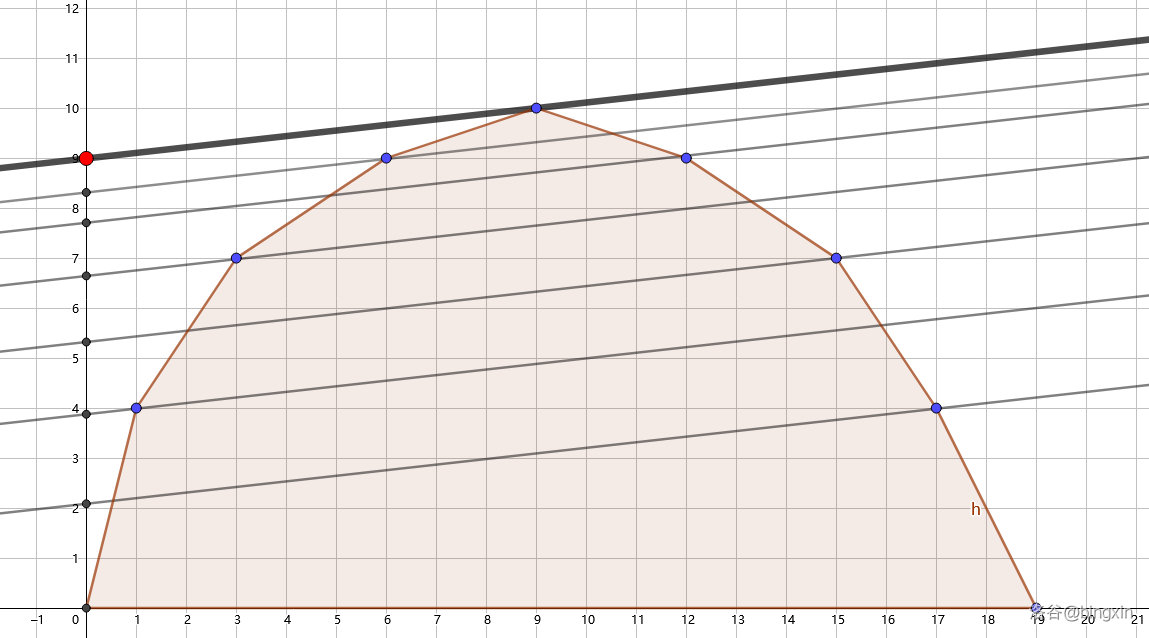
Part. 3 例题

可能有些没看懂，先来看一道例题：[国家集训队]Tree Ⅰ，简单且能体现 wqs 二分的大部分思想。

题意很清楚，给定一些边，颜色为白色或黑色，求最小生成树，限制条件就是最后的生成树恰好有 \(k\) 条白边。

可以看到，边就相当于上面的物品，\(k\) 条白边就相当于恰好要选的次数。我们对于没有数量限制的情况很好求，但有了 \(k\) 后我们就要考虑白边的数量和此时最小生成树的权值和，为了方便表示，我们将它设为 \(f(i)\) 。

这个 \(f(i)\) 怎么来的？跑 \(\text{Kruskal}\)
\(\text{Kruskal}\) 怎么控制边的选取？贪心
我们怎么调整这些边，使满足题意，有 \(k\) 条边？
注意到：
sort(e + 1, e + m + 1, cmp);
由此可知，边权越小越靠前，所以我们可以给白边附上一个权，来调整他们的位置。

例如当无任何调整时最小生成树上有 \(4\) 条白边，但我们的 \(k=3\)，那么可以全部加上一个数，然后某些条白边的 \(w\) 突然比某些黑边大了，我再跑 \(\text{Kruskal}\) ，更新之后的最小生成树就会把某些变大的白边扔到后边去，替换成黑边，那么此时白边条数就减少了，最后把加的这个数减掉就行了（你问白边数目少了怎么办？）

于是这个权值可以二分求解
最后我觉得这个算法最迷人的地方就在于阐述时用了一堆计算几何的知识但最后写代码不需要一点计算几何（

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 1e5 + 5;
int n, m, k;
int u[N], v[N], w[N];
bool c[N];

int f[N];
inline int find(int x) { return f[x] == x ? x : f[x] = find(f[x]); }

struct
{
    int u, v, w;
    bool c;
} e[N];
int cnt, ans;
void check(int x)
{
    cnt = ans = 0;
    for (int i = 1; i <= m; i++)
        e[i] = {u[i], v[i], w[i] - x * !c[i], c[i]};
    sort(e + 1, e + m + 1, [](const auto &x, const auto &y)
         { return x.w < y.w || (!(y.w < x.w) && x.c < y.c); });
    iota(f, f + n, 0);
    for (int i = 1; i <= m; i++)
    {
        int fu = find(e[i].u), fv = find(e[i].v);
        if (fu == fv)
            continue;
        f[fv] = fu;
        cnt += !e[i].c, ans += e[i].w;
    }
}

signed main()
{
    ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    cin >> n >> m >> k;
    for (int i = 1; i <= m; i++)
        cin >> u[i] >> v[i] >> w[i] >> c[i];

    int l = -100, r = 100;
    while (l < r)
    {
        int mid = (l + r) >> 1;
        check(mid);
        if (cnt >= k)
            r = mid;
        else
            l = mid + 1;
    }
    check(l);
    cout << (ans + l * k);
    return 0;
}