dfs和bfs遍历图
3、遍历
- bfs ： Breadth first search
思路：
和二叉树的层序遍历很像，应用队列，一层一层的遍历
注意在图中，下一层指的是 此节点一步能到达的位置
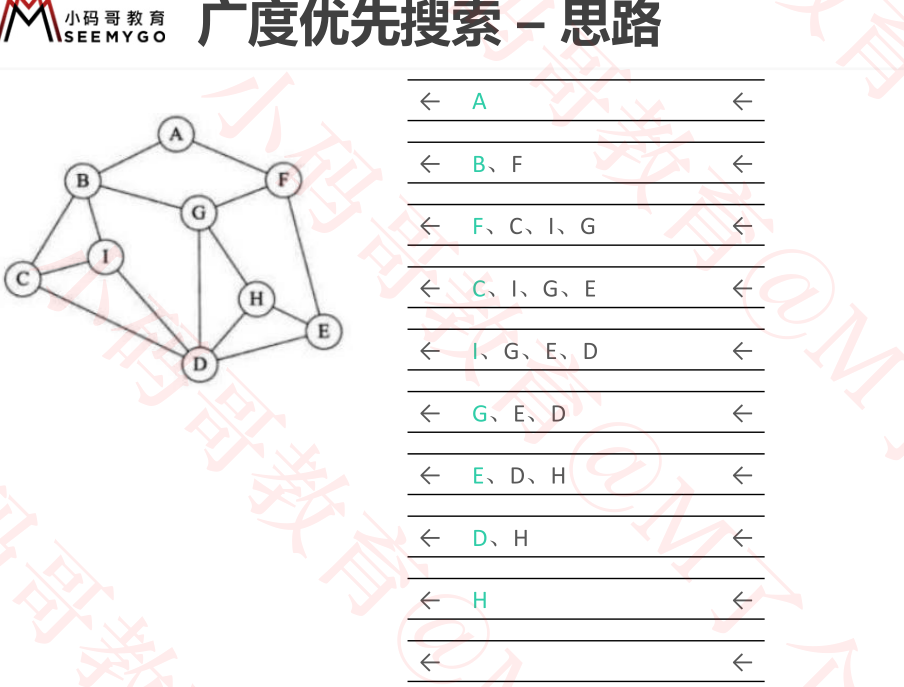
不过这里变成了遍历顶点的 outEdges 依次入队，不过当图有环的时候可能重复出现斯循环，所以我们用set来去重！
- 代码
//遍历图，使用BFS算法！
public void bfs(V value) {
Vertex<V, E> vertex = vertices.get(value); //遍历的起点
if (vertex == null) return;
Queue<Vertex<V, E>> queue = new LinkedList<>(); //使用队列，java中队列由双向链表实现
Set<Vertex<V, E>> set = new HashSet<>(); //用set去重，怎么去？入队的同时在set中加上
queue.offer(vertex);
set.add(vertex);
while (!queue.isEmpty()) {
Vertex<V, E> poll = queue.poll();
System.out.println(poll.value);
for (Edge<V, E> outEdge : poll.outEdges) { //outEdges的终点就是下一层节点
if (set.contains(outEdge.to)) continue;
queue.offer(outEdge.to);
set.add(outEdge.to);
}
}
}
- DFS ： depth frist search
- 递归实现
思路：我们在想递归的时候千万不要往深了想，其实还是很简单的
- 代码：
//深度优先搜素,相当于前序遍历！
@Override
public void dfs(V begin) {
Vertex<V, E> vertex = vertices.get(begin);
if (vertex == null)
return;
dfs(vertex, new HashSet<>());
}
private void dfs(Vertex<V,E> vertex, Set<Vertex<V, E>> set) {
if (vertex == null)
return;
System.out.println(vertex.value);
set.add(vertex);
for (Edge<V, E> outEdge : vertex.outEdges) {
if (set.contains(outEdge.to)) continue;
dfs(outEdge.to, set);
}
}
又要使用set去重和上面的去重思路差不多！
总结：如何理解循环中的递归：
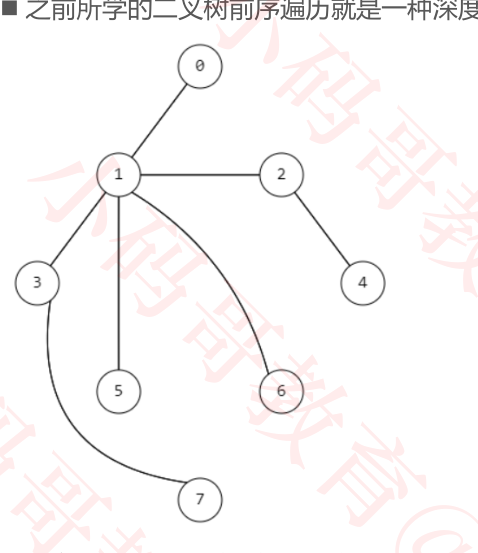
如果是上述图我们从 节点 1 开始遍历：上来就会进入for循环，遍历了
dfs(3) 、 dfs(5) 、dfs(2) 、dfs(0)
进入dfs(3) 又是进行深度优先搜索，遍历 7 ，遍历完3，才会遍历 dfs(5) ···
就这么理解就行！
3、DFS非递归实现
就是先序遍历，选一条变向下走到极致在回头！
所有的递归都能转化成迭代，不过有的很难
为什么呢？
因为递归就是函数JVM压栈出栈的过程，而我们数据结构中的栈也是这个特点，所以很多复杂的递归都能使用栈和迭代来实现!
代码：主要是想到要用到栈，结合栈先进后出的特点进行深度思考！
public void dfs(V begin, Visitor<V, E> visitor) {
if (visitor == null) return;
Vertex<V, E> vertex = vertices.get(begin);
if (vertex == null) {
return;
}
Stack<Vertex<V, E>> stack = new Stack<>();
Set<Vertex<V, E>> visited = new HashSet<>();
stack.push(vertex);
if (visitor.visit(vertex.value)) return;
visited.add(vertex);
while (!stack.isEmpty()) {
Vertex<V, E> pop = stack.pop();
for(Edge<V, E> edge : pop.outEdges) {
if (visited.contains(edge.to)) continue;
stack.push(pop);
stack.push(edge.to);
if (visitor.visit(edge.to.value)) return;
visited.add(edge.to);
break; //这个break才是最关键的，我们只会选择一条边向下钻
}
}
}
总结：set是无序的所以不知道先遍历那条边，为什么要 把from 和 to都放进去在Break，我们每次只访问to节点的值···
