最小生成树☞kruskal算法

最小生成树☞kruskal算法:

今天总结一下最小生成树的另一种方法: kruskal算法。它与prim的算法的思路有所不同，prim算法利用了切分定理，而它的思路比较简单，就是从剩下的边中不断寻找最短边，最终构成一棵树。
下面我们首先来分析一下:

思路分析

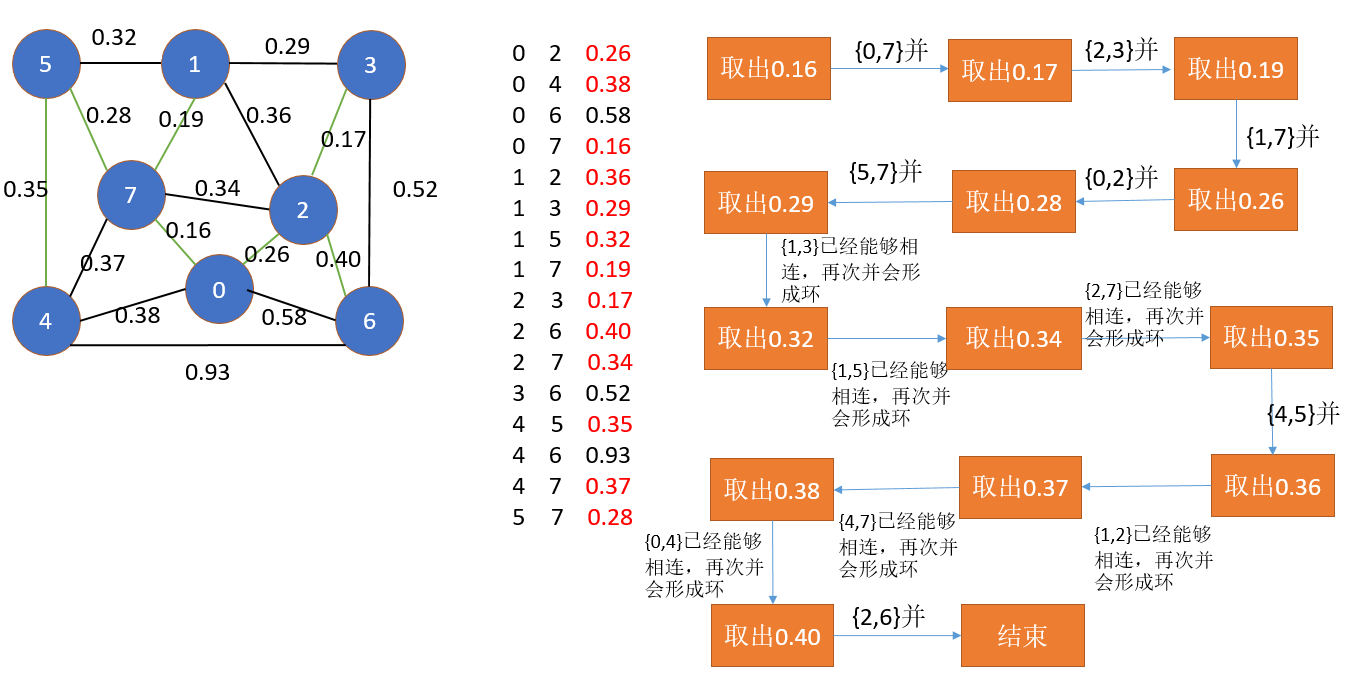
从图中的步骤我们可以看出,我们需要首先把这张图的所有边存放到一种数据结构中，每次取出权值最小的那一条，如果这条边的两个定点通过其它点能够连接到一块，那么它就不是最小生成树的边，因为这样它会形成环；如果这两个顶点不能够通过其它顶点连到一块儿,那么它就必然属于最小生成树的一条边,因此我们还需要另外一种数据结构来判断任意两点是否是连接的，也就是并查集；而对于边的存储，我们可以使用最小堆，下面我们代码来实现一下。

代码实现:

public class KruskalMST<Weight extends Number & Comparable > {	
/**图的引用*/
  private WeightedGraph<Weight> G;
  /**最小堆*/
  private MinHeapWeight>> minHeap;
  /**生成最小树所有的边*/
  private VectorWeight>> mst;
  /**最小生成树的权值*/
  private Number mstWeight;

 public KruskalMST(WeightedGraph<Weight> g) {
      G = g;
      mst = new Vector<>();
      this.minHeap = new MinHeap<>(G.E());
    /**将图中的所有边存放到一个最小堆中*/
      for(int i=0;i<G.V();i++){
	for(Edge<Weight> e : g.adj(i)){
	   if(i<e.getOther(i)){             //避免重复将边加入到堆中
	         minHeap.insert(e);
                 }
	      }

	}
	/** 创建一个并查集, 来查看已经访问的节点的联通情况，如果是联通的必然会构成一个环*/
  UnionFind unionFind = new UnionFind(G.V());
  while (!minHeap.isEmpty()&& mst.size() < g.V() - 1 ){
	 Edge<Weight> e = minHeap.pop();
	       /**如果两个顶点是连接的。则仍掉这条边*/
         if(unionFind.isConnected(e.a(),e.b())){
	  continue;
        }
          mst.add(e);
        /**将两个顶点并起来*/
         unionFind.unionElements(e.a(),e.b());
   }
        mstWeight = mst.get(0).wt();

        for(int i=1;i<mst.size();i++){
	     mstWeight =  mstWeight.doubleValue() + mst.get(i).wt().doubleValue();
         }

   }
	  /**返回构成最小生成树边的集合*/
  public VectorWeight>> getMst(){
      return mst;
  }

	/***返回最小生成树的权值*/
  public Number getMstWeight(){
      return mstWeight;
  }