Ng ML笔记
目录
二、逻辑回归(Logistic Regression,LR)
一、线性回归
1,假设函数、代价函数,梯度下降
假设函数h,代价函数J为平方误差和

梯度下降算法,不断更新参数的值,使其延梯度的反方向变化,不断收敛至一个局部最优解

2,特征处理
如果每个特征的范围相差的很大, 梯度下降会很慢. 为了解决这个问题, 我们在梯度下降之前应该对数据做特征归缩放(Feature Scaling)处理, 从而将所有的特征的数量级都在一个差不多的范围之内, 以加快梯度下降的速度.
![]()
或者除以max-min进行均值归一化,适当即可
3,代价函数和学习速率



通常可以考虑尝试些学习率:𝛼=0.01 0.03 0.1 0.3 1 3 10
4,特征和多项式回归

5,正规方程
因为多变量线性回归的代价函数是凸函数,所以有最优解,令其每一个theta在所有数据集上的导数等于0,可得其解


正规方程与梯度下降法比较

对于不可逆的情况,则尽可能的删除多余的特征使其可逆,或计算伪逆
二、逻辑回归(Logistic Regression,LR)
1,假设函数

![]()

2,代价函数
如果用线性回归中的代价函数,则由于假设函数的变化,代价函数是一个非凸的函数,定义新的代价函数,是一个凸函数


3,梯度下降算法
与多变量相同,导数部分相同,证明见pdf。虽然算法看上去是一样的,但是假设函数不一样

4,高级算法
除了梯度下降算法以外,还有一些常被用来令代价函数最小的算法,这些算法更加复杂和优越,而且通常不需要人工选择学习率,通常比梯度下降算法要更加快速。这些算法有: 共轭梯度 Conjugate Gradient、局部优化法 (Broyden fletcher goldfarb shann,BFGS)、有限内存局部优化法(L-BFGS)。逻辑回归也需要特征缩放,提高梯度下降的收敛速度。
用逻辑回归也可以使用一对多的方法进行多分类
三、正则化
1,过拟合

如何处理

2,正则化

因为如果我们令𝜆 的值很大的话,为了使 Cost Function 尽可能的小,所有的 𝜃 的值(不包括 𝜃0)都会在一定程度上减小。
但若λ的值太大了 那么 𝜃(不包括 𝜃0)都会趋近于 0,这样我们所得到的只能是一条平行于 𝑥轴的直线。
所以对于正则化,我们要取一个合理的𝜆 的值,这样才能更好的应用正则化。
3,正则化线性回归
代价函数加上正则化项,梯度下降加上正则化项

4,正则化逻辑回归
代价函数加上正则化项,跟线性回归相似,只是假设函数不同,梯度下降算法相同


四、神经网络
1,正向传播算法
每一个单元都是一个逻辑回归



![]()
![]()
2,反向传播算法
代价函数

其中的sl+1下错了应为下标,表示第l+1层的单元数,正则化项为所有theta,不包括偏置单元的参数
计算偏导数,先计算每一层的误差
![]()

在计算每一个参数的偏导数

以上仅仅是对于一个数据,需要把所有数据的加起来,最后得到的偏导数为下面,正则化项也要除以m

3,梯度检验、随机初始化



五、应用机器学习的建议
当测试假设函数时,误差很大,可以尝试以下方法

判断是否过拟合:70%作为训练集,30%作为测试集。对于线性回归,使用代价函数计算误差;对于逻辑回归,可以使用代价函数计算误差,也可以计算误分类比率
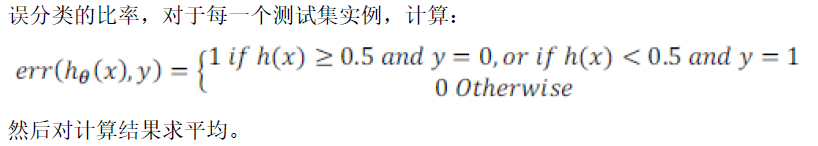
在多个模型中选择一个模型,60%作为训练集,20%作为交叉验证集,20%作为测试集,训练好后用验证集选择较小的误差模型,然后用测试集测试误差,才能更好的表示其泛化能力。
诊断偏差和方差,偏差/欠拟合、方差/过拟合

正则化防止过拟合,lambda小时欠拟合,大时欠拟合,交叉验证集误差先减小后增大。选择交叉验证集最小的时候的值

学习曲线,高偏差/欠拟合时,增加训练数据集没有什么效果;高方差/过拟合时,增加训练数据集可以提高算法效果。


查准率和查全率,查准率分母是所有预测为真的样本,表示预测为真并正确的样本在预测为真的样本中的比例;查全率分母是实际为真的样本,表示预测为真并正确的样本中在实际为真的样本中的比例。
对于不同的查准率和召回率阈值,会有不容的查准率和召回率,这个时候使用F1 score选择较大的作为阈值,避免极端


六、支持向量机SVM
1,代价函数
相比于逻辑回归的代价函数,SVM的代价函数在theta*x>1或小于-1时代价为0,也即是对于预测而言,他们都是肯定是正或负,不是概率,而仅仅要求theta*X>0 我们就判定它为正,但在代价函数中却要求它大于1,相当于在SVM中嵌入了一个额外的安全因子,或者说安全的间距因子。


当C非常大时,SVM的代价函数努力是正则化项变小,也即是使theta的二范数(长度)变小,决策边界如下。那么x在theta上的投影p就需要变大,那么分类器的法线就会向类中心靠拢,以使得投影p变大,theta最小。那么就导致最终的分类参数对于各类是最大间隔的。


当theta*x>0时判定是正分类,其他为负分类
2,核函数
在以上SVM中,如何选择特征呢?答案是使用核函数。核函数是将原训练集的每一个训练样本映射到另外一个训练样本。映射方法是使用核函数计算相似度,计算相似度的对象是每一个训练样本。设有m个训练样本作为地标(landmark),那么参数就是m+1个(包含截距theta0)。计算每一个样本到地标的相似度作为新的特征,这样还是有m个样本,每个样本有m个特征(或加上x0=1)。核函数的思想是包含了一个样本距其他样本的所有距离,每个距离时样本的一个特征,距离它自己是1(高斯核函数)。然后应用到SVM中,


3,参数的影响,其他核函数,如何选择分类算法
当特征n非常多,训练集m非常少时,用线性核函数,也即是不使用和核函数,因为特征已经足够多了。


逻辑回归和不带核函数的SVM的代价函数时凸函数,容易找到最优解,适用于特征较多,训练数据少和特征少,训练数据多的情况,因为特征较多时没有必要使用高斯核函数的SVM。而训练数据m多时,使用高斯核函数SVM会很慢。
当特征较少,而训练数据又不太多时,使用高斯核函数的SVM
以上情况神经网络都会有很好的表现,但是训练神经网络可能非常慢,而且神经网络的代价函数是非凸的,只能求局部最小值。

SVM进行多分类需要使用一对多的方法,逻辑回归、线性回归也是。神经网络可以直接进行多分类。
七、k-means聚类算法
1,在样本中随机选择k个样本作为簇中心,然后计算每一个样本到簇中心的距离并把他们归类到k中;
2,重新计算每一个簇的簇中心。直到簇中心不在变化,表示收敛。
为了得到更好的分类,多次随机初始化,选择代价函数较小的那个分类决策。通常在k不超过10时,随机初始化
50-1000次会得到比较好的分类结果。但是如果k比较大,那么随机初始化多次效果不大。


利用肘部法则确定分类数k,但并不常用,因为大部分的时候如右图所示并不会给出一个明显的答案。通常还是根据需求选择k。

八、主成分分析PCA-数据降维
动机:数据压缩(减少内存使用;让学习算法运行的更快)、数据可视化(2D,3D)
PCA与回归的区别:PCA是最小化距离(无标签),回归是最小化y(有标签)
错误:1> 使用PCA防止过拟合,不如使用正则化,原因是PCA这是近似的丢掉一些特征,不考虑任何与结果变量有关的信息,因此有可能丢失非常重要的特征。而正则化处理时,会考虑到结果变量,不会丢掉重要数据。2> 默认将PCA作为学习过程的一部分,虽然很多时候有效果,最好还是从所有原始特征开始,在必要的时候(算法运行太慢或占用内存)才考虑PCA。
优点:PCA的一大优点是对数据降维的处理,对新求出的主元向量的重要性进行排序,根据需要提取前面重要的部分,将后面的省去,达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保留了原数据的信息。另一个优点是它是无参数限制的,在PCA的过程中完全不需要人为的设定参数或根据任何经验对计算进行干预,结果与用户无关
算法:1> 均值归一化,进行特征缩放;2> 计算协方差(向量表示1/m*x'*x);3> 计算协方差的特征向量(奇异值分解svd, 特征向量eig),根据需要进行降维,选取需要的特征向量,转置乘以原数据x得到降维后的特征z。这样做确实是使数据到一定维度的距离最小。


重建原数据:根据压缩后的数据和映射的特征向量可以近似得到原维度的数据:用特征向量乘新特征z近似得到x。因为在特征向量中丢掉了部分不重要的向量信息,所以在恢复时是近似恢复。

如何选取降维数k:从k等于1开始,计算平方误差占训练集方差的比例,表示被扔掉的信息比例,通常小于1%就可以了。也可以使用特征值计算。


九、使用高斯分布进行异常检测
一元高斯分布:


评估算法:异常检测是一种非监督学习算法,因此我们无法根据变量y来告诉我们数据是否真的异常。我们需要另外一种方法来帮助检验算法是否真的有效。从带有标记的数据着手,选取一部分作为训练集,剩下的正常数据和异常数据混合的构成交叉验证集和测试集。用训练集计算模型参数;用交叉验证集设置不同的epslon,计算TP,TN,FP,FN,计算F1score,选择比较大的;最后使用测试集进行预测,计算TP,TN,FP,FN,计算F1score。

特征分布:异常检测假设特征符合高斯分布,如果数据不是高斯分布,最好还是将数据转换为高斯分布工作,但是最好还是将数据转换成高斯分布,例如使用对数函数: 𝑥=𝑙𝑜𝑔(𝑥+𝑐),其中 𝑐 为非负常数; 或者 𝑥=𝑥𝑐 𝑐为 0-1 之间的一个分数,等方法。
误差分析:一些异常的数据可能也会有较高的p(x)值,因为被算法认为是正常的,这时候可以通过误差分析,分析那些被算法错误预测为正常的数据,观察能否找出一些问题,从问题中发现一些新特征,增加这些新特征来更好的检测。
多元高斯分布


区别:多元高斯分布可以捕捉特征之间的联系,但是当特征很大时,计算代价很高(求逆,求行列式),而且必须要求数据集远大于特征数,才可以有效的拟合参数。
一元高斯分布计算代价低,不能捕捉特征之间的相关性,但可以通过特征组合的办法来解决。一元高斯分布是多元高斯分布在协方差除对角线意外的值为0的特殊情况。
十、推荐系统
1,基于内容的推荐系统
已知电影的特征,训练用户的参数,然后预测用户对电影的评分。


2,协同过滤
假设我们已知用户的特征,也可以训练出电影的特征

如果没有用户的特征,也没有电影的特征,那么协同过滤算法可以同时学习这两者

虽然学习到的特征不是人能读懂的,但是可以用这些数据作为给用户推荐的依据
将结果矩阵化,叫低秩矩阵分解。在应用时,避免某一用户对电影的评分全为0,可以先对电影评分进行归一化,然后对预测结果加上均值。
十一、大规模机器学习
1,增加训练数据是否有效
首先选择少量的训练数据进行训练,画出学习曲线

2,随机梯度下降SGD
当训练集很大时,可以尝试随机梯度下降SGD代替批量梯度下降BGD,1>将所有数据随机打乱,2>对每一个数据进行梯度下降,也即是每次只使用一个数据进行梯度下降。3> 通常这样从头到尾重复1-10次(根据训练集的大小而定)。这样的问题是并不是每一步都是朝着正确的方向迈出的,因此,虽然算法会走向全局最小值的位置,但是无法站在最小值那一点,而是在附近徘徊。

3,mini-batch gradient descent
有可能比SGD运行的更好,如果向量化的方式循环的比较好的话,同时支持并行运算

4,SGD的学习速率alpha
通过画迭代次数与误差的图观察收敛性,在每一次更新参数之前计算出一个代价,更新1000次后计算平均代价,然后画出平均代价与迭代次数的图,进而调整学习速率。使用这种方法不用定时的扫描整个训练集,就可以保证SGD正在正常运转和收敛,也可以用来调整学习速率。
5,在线学习,MapReduce并行计算
本文来自博客园,作者:Bingmous,转载请注明原文链接:https://www.cnblogs.com/bingmous/p/15643744.html





