贝叶斯公式与最大后验估计(MAP)
1, 频率派思想
频率派思想认为概率乃事情发生的频率,概率是一固定常量,是固定不变的
2, 最大似然估计
假设有100个水果由苹果和梨混在一起,具体分配比例未知,于是你去随机抽取10次,抽到苹果标记为1, 抽到梨标记为0,每次标记之后将抽到的水果放回
最终统计的结果如下:
苹果 8次,梨2次
据此,我可以推断出苹果的比例吗?
最大似然估计看待这个问题的思路是:
1、1、0、1、1、0、1、1、1、1
每次抽样都是独立的随机过程,抽到苹果的概率为 p, 抽到梨的概率为 1 - p,那么抽到8次苹果,2次梨的概率为:
$P_{x} = p^{8}(1 - p)^{2}$
为什么我会抽到8次苹果、2次梨,为什么不是7/3次或其他的组合形式,这背后肯定有股神秘力量(上帝)在给我暗示:你这一次抽到的是8/2的组合,你下一次也极有可能还是会抽到8/2组合,你每次都会以最高的概率抽到 8/2的组合,因为事实的真相就是8/2组合
有了这个思想,我们可以求解, 当p = ? 时, 以8/2组合抽取,概率 $P_{x}$ 是最大的(极大似然)
$\begin{equation}
P_{x} = \mathop{\arg\max}_{p} \ \ p^{8}(1-p)^{2}
\end{equation}$
剩下的就是 取对数 -> 求导 -> 求0值, 得到
p = 80%
再来回顾一下解题的思路: 做实验之前,p 就是一固定的数值了(虽然具体值是什么我们还不知道),通过实验,我们得到了上帝的暗示,采用某种方式(最大似然估计),来找到这个p
3, 贝叶斯思想
贝叶斯派将概率解释成对事情发生的信心,是一个变量,有很大主观成分
先来看一下贝叶斯公式的定义:
$p(θ|x) = \frac{p(x|θ)p(θ)}{p(x)} = \frac{p(x|θ)p(θ)}{\sum^{k}_{i = 1}{p(x|θ_{i})p(θ_{i})}}$
只看前半部分:
$p(θ|x) = p(θ)\frac{p(x|θ)}{p(x)}$
贝叶斯的思想过程是这样的:
起初我并不知道θ的具体值是多少,同时θ还是一变量, 它的取值服从某种概率分布,比如说抛硬币实验,假如我说投硬币正面概率为0.6(个人主观臆断,有出错的可能), 在说这句话的同时,其实还有隐台词: 投硬币得到正面的概率θ是一个飘忽不定的值,它最有可能取0.6,其次还可能为0.4、0.5、0.3、0.7.....,只是取其他值的可能性比较小,θ(正面的概率)的概率分布可能近似于一个高斯模型。
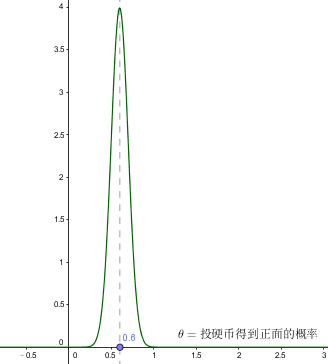
现在进行第一次投硬币,假如结果为正,从直觉上看,本次投到的结果为正,将会大大增加我对θ(投币结果为正)的信念,具体是怎么影响的呢?
首先来看$p(x|θ)$, 通过前面的讲解,我们知道这是一个似然函数模型,意为: 我在用这套θ参数的情况下,将会以多大概率(likehood)取到当前这个样本
当θ = 1.0时, $p(x|θ) = θ^{1}(1 - θ)^{0} = 1$
当θ = 0.6时, $p(x|θ) = θ^{1}(1 - θ)^{0} = 0.6$
当θ = 0.5时, $p(x|θ) = θ^{1}(1 - θ)^{0} = 0.5$
当θ = 0.0时, $p(x|θ) = θ^{1}(1 - θ)^{0} = 0$
再来看 $p(x)$,$p(x)$ 代表的是样本x发生的实际概率, 结合本例来讲,这里$p(x = 1)$代表的是取到一次正面的概率,通过大量实验,可以算出 $p(x = 1) = 0.5$(地球人都知道,随机抛一个硬币,正面朝上的概率为0.5)
现在把他们的关系整理一下:
|
θ |
P(θ) |
p(x|θ) |
P(x) |
p(x|θ)/ P(x) |
P(θ)*p(x|θ)/ P(x) |
|
1 |
0 |
1 |
0.5 |
2 |
0 |
|
0.6 |
3.99 |
0.6 |
0.5 |
1.1 |
4.389 |
|
0.5 |
2.42 |
0.5 |
0.5 |
1 |
2.42 |
|
0 |
0 |
0 |
0.5 |
0 |
0 |
如果我们将第四列用下面形式表示:
$\frac{p(x|θ)}{P(x)} = \frac{likely}{really} = \frac{本参数下的似然概率}{实际出现的概率} = 信心增强系数$
那么我们可以将贝叶斯公式理解为:
$已知x前提下对θ的估计 = 对θ的初步估计 * 信心增强系数$
修正倍数 = 1时,表示本参数下的预测概率 = 实际出现的概率,对θ的初步估计比较适中,不需要调整
修正倍数 > 1时,表示本参数下的预测概率 > 实际出现的概率,大大增强了我的信心,对θ的确定性我觉得可以再大点
修正倍数 < 1时,表示本参数下的预测概率 < 实际出现的概率,对我是个沉重的打击,对θ的确定性我也没那么多把握了
结合本实验:
假设 θ = 1,即抛硬币为正的概率为1(永远都得到正面), 但是假设毕竟是假设,我对此也很没把握,所以p(θ) = 0(或接近0的值),通过一次实验,观察到硬币果然是正,这个实验结果增加了我对θ = 1(正的概率为1)的信念,增强系数为2
假设 θ = 0.6,对此我有很大把握,所以p(θ) = 3.99,于是我用θ = 0.6这一套参数去做了一个似然估计,发现似然估计比真实的概率更好(更接近投一次硬币为正这个事实),于是乎,我更加坚信θ = 0.6,增强系数为1.1
假设 θ = 0,对此我又没多大把握,所以p(θ) = 0(或接近0的值),通过一次实验,观察到硬币是正,我觉得θ = 0(投硬币为正概率为0)更不靠谱了,于是对我原来的把握度,我需要再降低一个档次,增强系数为0
现在我进行第二次试验,再次出现正面为上的结果
|
θ |
P(θ) |
p(x = 1,1|θ) |
P(x) |
p(x= 1,1|θ)/ P(x) |
P(θ)*p(x|θ)/ P(x) |
|
1 |
0 |
1 |
0.25 |
4 |
0 |
|
0.6 |
3.99 |
0.36 |
0.25 |
1.44 |
5.7456 |
|
0.5 |
2.42 |
0.25 |
0.25 |
1 |
2.42 |
|
0 |
0 |
0 |
0.25 |
0 |
0 |
可以看到,我对θ = 1的信心是越来越大了,对其他case的信心也有所调整
第三次实验,抛硬币得到反面为上的结果
|
θ |
P(θ) |
p(x = 1,1,0|θ) |
P(x) |
p(x= 1,1,0|θ)/ P(x) |
P(θ)*p(x|θ)/ P(x) |
|
1 |
0 |
0 |
0.125 |
0 |
0 |
|
0.6 |
3.99 |
0.144 |
0.125 |
1.152 |
4.59648 |
|
0.5 |
2.42 |
0.125 |
0.125 |
1 |
2.42 |
|
0 |
0 |
0 |
0.125 |
0 |
0 |
像这样我们可以重复做100次实验,假设得到正的次数为51次,反的次数为49次
|
θ |
P(θ) |
p(x|θ) |
P(x) |
p(x|θ)/ P(x) |
P(θ)*p(x|θ)/ P(x) |
|
1 |
0 |
0 |
$0.5^{51}0.5^{49}$ |
0 |
0 |
|
0.6 |
3.99 |
$0.6^{51}0.4^{49}$ |
$0.5^{51}0.5^{49}$ |
0.195 |
0.777 |
|
0.5 |
2.42 |
$0.5^{51}0.5^{49}$ |
$0.5^{51}0.5^{49}$ |
1 |
2.42 |
|
0 |
0 |
0 |
$0.5^{51}0.5^{49}$ |
0 |
0 |
随着样本的增多,对$p(θ|x)$会越来越集中,且最终的结果与实验数据保持一致(θ = 0.5附近)

经过100次抛币实验后的后验概率分布图如上所示,最大概率大概在 θ = 0.53 的地方取得
现在来看一个问题:在我们不断尝试调整θ的过程中,列表其他项都会跟着改变,唯独p(x)那一列不会改变,这里需要用频率派的唯物主义观点来解释,结合本实验,p(x)代表取到当前实验数据的概率大小,这是客观事实,只能通过大量实验统计或者借用上帝视角把它算出来(没错,我就是作弊了)
既然p(x)是固定不变的值,那么我们就可以得到下面结论:
$p(θ|x) ∝ p(θ)p(x|θ)$
这是理解最大后验估计(MAP)的关键
再来看贝叶斯思想的另外一个例子:
一机器在良好状态生产合格产品几率是 90%,在故障状态生产合格产品几率是 30%,机器良好的概率是 75%。若一日第一件产品是合格品,那么此日机器良好的概率是多少?
根据韦恩图,我们可以很方便的解决这个问题
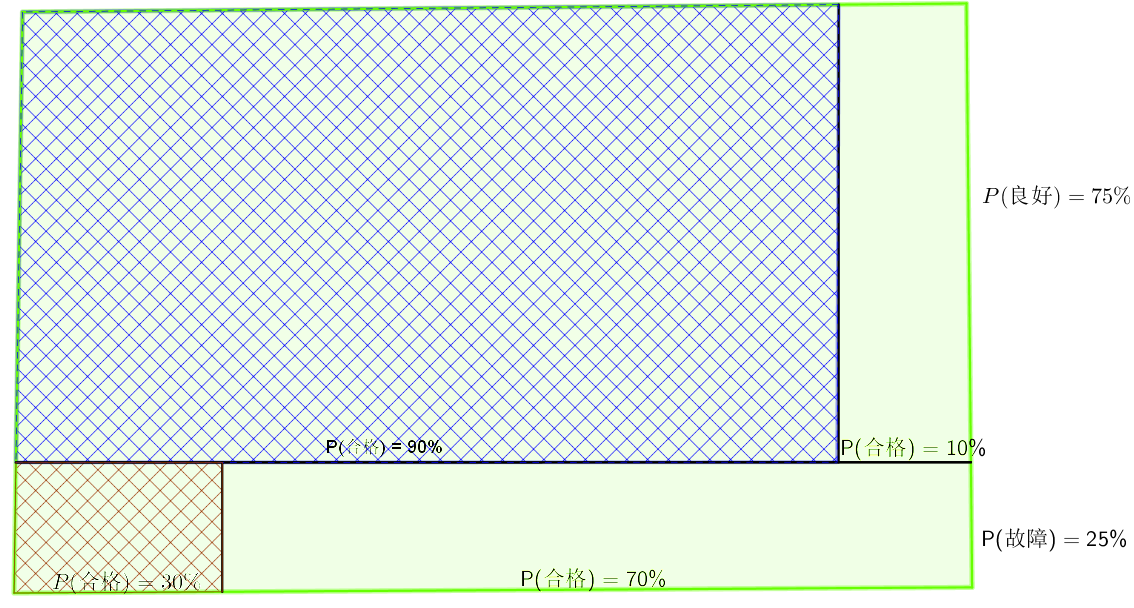
因为题目已经说了,第一件产品是合格品,因而问题的范围自然就落入了标网格的矩形范围内
现在要求的是在标网格的矩形范围内,找出蓝色网格的比例(机器良好的概率),剩下的就是求矩形面积之比了
对应的公式模型就是
$p(θ|x) = \frac{p(x|θ)p(θ)}{\sum^{k}_{i = 1}{p(x|θ_{i})p(θ_{i})}}$
这个模型又该怎么理解呢?结合本实例:
p(x|θ)p(θ)作为一个整体来看,它在本例中表示的意思就是: 我们现在关注于机器良好的情况,机器良好且生产良品概率为:
p(x|θ)p(θ) = 75% × 90% = 0.675
第一件产品是合格品,即 x = 合格
我们分析这个合格的来源,它有可能来自良好机器(75%)生产的(90%),也有可能来自故障机器(25%)生产的(30%),那么
p(x) = 75% × 90% + 25% × 30% = 0,75
两者相除的结果:
p(θ|x) = 0.9
观察这个过程,可以看到分子表达式是分母的一部分,相除可解释为求比例,导致产品合格的原因有多种,P(良好|合格)的意思是拿出来的是一件合格品,这件合格品是良好机器做出来的几率(良好机器生产合格品在整个合格品中的比例)。
$P(良好|合格) = \frac{P(良好)P(合格|良好)}{P(良好)P(合格|良好) + P(故障)P(合格|故障)}$
通过这种模型可以很轻易从另一个角度解释后验概率p(θ|x),如果偏要借用模板一的方法来理解,过程是这样:
最开始,我觉得机器良好的概率是75%,机器状态的概率分布如下所示:
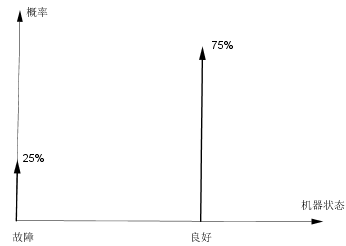
在相应状态,生产良品的概率(似然)如下:

注意这里的 θ = 机器状态,θ可能的取值只有故障、良好两种状态。现在我做了一个实验,发现是良品,于是我对机器是良好的信息将会有所调整:
$p(θ|x) = p(initial)\frac{p(likely)}{p(really)} = 75\%\frac{75\% × 90\%}{75\% × 90\% + 25\% × 30\%} = 0.9$
注意抛硬币实验中的 θ = 抛硬币为正的概率,是一个连续变量
机器生产实验的 θ = 机器状态,要么是良好,要么是故障,是一个离散变量
4, 最大后验估计(MAP)
有了前面对贝叶斯思想的描述,我们可以很容易理解最大后验估计(MAP)
θ是一个连续或离散的变量
p(θ|x)表示我取到了一个数值为x的样本
取$θ = θ_{1}$时,我将会以$p(x|θ_{1})$取到该样本,以这种方式取到样本x的概率占所有可能性p(x)的比例为$p(θ_{1}|x)$
取$θ = θ_{2}$时,我将会以$p(x|θ_{2})$取到该样本,以这种方式取到样本x的概率占所有可能性p(x)的比例为$p(θ_{2}|x)$
......................
于是我就想,这个θ到底是多少呢?我知道θ是随时在变的,我不可能捕捉到它的确切数值,但我可以猜出它最有可能的值,理由是:
我拿到了一组样本x,我觉得这肯定不是一种偶然,我以这种方式拿到样本x的概率一定是所有可能性p(x)中最大的,用数学符号简化一下就是:$p(x|θ)p(θ)$是$p(x)$中最大的,即$p(θ|x)$最大,反过来说,我知道了$p(θ|x)$的最大值,我就知道了θ最可能的取值,以这种思路求θ的过程就称为最大后验估计(MAP)
$\mathop{\arg\max}_{θ} p(θ|x) = \mathop{\arg\max}_{θ} \frac{p(x|θ)p(θ)}{p(x)} = \mathop{\arg\max}_{θ} p(x|θ)p(θ)$
其中: $p(θ|x) ∝ p(θ)p(x|θ)$
可以看出,最大后验估计与最大似然估计的思想方法还是存在很大的相似性的,不同的是:
最大似然估计是根据数据直接直接对θ进行估计
最大后验估计是在对θ进行估计之前,强加了一个可能性因素p(θ)
至于样本x的概率p(x),这是个一个客观存在(只有上帝知道,或做实验取逼近)的东西,有它没它对估计值没有影响
实际上,p(θ) = const是,最大似然与最大后验估计的结果就是一致的,原因是,我不知道 θ 的值为多少,我也不妄加揣测,我认为它的可能性都是相同的,这样,我估计和没估计其实没什么差别(就好比某经济学家说明天股市可能大涨,也存在下跌的空间,那说了等于没说嘛)。
另外,p(θ)带有极强的主观臆断,既然是主观的,那就有可能犯错,如果我犯错了怎么办呢,解决办法就是大量实验,比如刚才的投币实验,虽然我先前对p(θ) = 0.6的估计是一个错误值,但是通过大量实验,会对我的估计值进行修正,最终与最大似然估计值接近
如果有一个固执的贝叶斯概率论者坚持认为
$f(x)=
\begin{cases}
0,&\quad \text{θ =1}\\
1,&\quad \text{θ != 1}
\end{cases}$
那不管怎么做实验都没招了~
5, 问题与探讨
关于贝叶斯思想与最大后验估计,我讲的就这么多,在理解贝叶斯的过程中,我很多次掉进了惯性思维的坑,通过不断思考对比,有些我已经找到问题的答案,有些还没有,现在拿出来给大家分享,有很多只是我的个人见解,不一定正确,希望大家纠正。
第一个问题,网上有很多都用下面模型来描述贝叶斯思想:
$p(癌症|阳性) = \frac{p(癌症)p(阳性|癌症)}{p(癌症)p(阳性|癌症) + p(非癌症)p(阳性|非癌症)}$
直接上,我们觉得检查出阳性的人基本上就完蛋了,但是通过贝叶斯分析,知道事实并不是这样的,同时我们还知道了其中的原因:
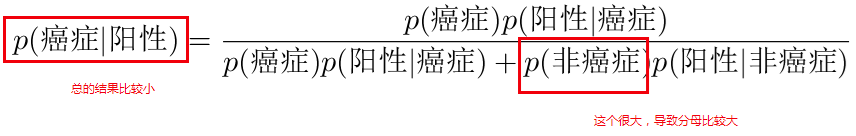
这里,我有一个疑惑,讲述最大后验估计时,我们说分母 p(x)对估计的结果不会造成影响,但是这里的分母确确实实影响了我们的判断,何解?
我觉得这个疑问的产生主要是混淆了贝叶斯公式与最大后验的研究对象。
贝叶斯公式说:我给你一组实验数据x(阳性), 你给我找出条件下θ(癌症)的概率p(θ|x)
最大后验估计说:我给你一组实验数据x(阳性),你给我猜一猜θ到底是得癌症还是未得癌症的几率大,即取p(θ|x)最大者
贝叶斯公式研究的对象是p(θ|x),这个是跟分母有关的
最大后验估计研究的对象是θ,这个跟分母是没有关系的
为什么检查出阳性,人们总会得出得癌症的错觉呢?
我觉得这是一个比较有意思的心理问题,惯性思维的思考过程是这样的:得癌症一般都是能检查出阳性的,那反过来,检查出阳性那就是的癌症了
思维上的局限性限制了我们对问题的判断,实际上生活中我们会经常犯这样的错误
孩子考试不好,我们是不是会经常责怪孩子不努力,而不反思是不是自己没有好的引导,老师没有教好,或者这个东西根本不是小孩的兴趣方向
女朋友吵架了,我们是不是经常会觉得她脾气不好,而不想是不是自己对她不关心,或者最近压力太大了?
。。。。。。。。

第二个问题,机器生产实验中,题目说p(良好) = 75%,按照贝叶斯公式的理解,这里不应该是一个带有主观臆断的先验概率吗?怎么是一固定值了?而且分母不是做实验做出来的吗?这里怎么直接算出来了?
其实,这里说机器良好的概率为75%(p(θ) = 75%),就是借用了上帝视角的说法,分母也是作弊算出来的(对比抛硬币实验,如果我一开始就开启上帝视角,那么正面朝上的概率分布p(θ)将是以0.5为中心,无穷大的脉冲,这样,做不做实验,都不会影响我对θ取值的信心了)。

第三个问题,抛硬币模型与机器生产概率模型的对比:
机器良好/故障 —— 硬币正/反
抽检结果得到合格 —— 随机抛出,得到正面
按照这种对应方式,他们应该是处于同一个模型的问题,为什么一个是离散问题,一个是连续问题?
现在假如使用离散模型来分析抛硬币实验:

分析在不同朝向下的似然概率:

两者相乘,会是一种什么结果?
如果这都还能接受,那么我再增加一次实验, 样本 x = 正面、正面、反面,这样在给定 x 的前提下, 不论θ = 正,还是θ = 反, 似然概率 p(x|θ) 都只能为0了(假设硬币是正,是不可能得到x = 反的样本的),到底是哪里搞错了?
贝叶斯思想是一种思维模式——由结果找原因,我们画后验概率p(θ|x)的分布图时,横轴始终是原因θ,纵轴始终是因果关系的比重,问题是,你选的原因是对的吗?或者你选择的原因会导致这种结果吗?
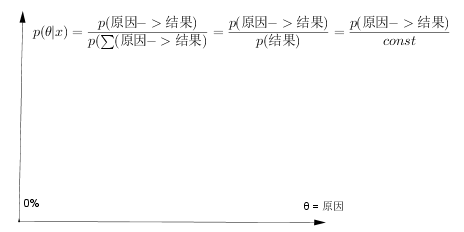
比如刚才的硬币实验,我的原因 = 硬币为正,会导致 x = 正、正、反的结果吗?
明白了这个问题,我们再讨论一下如何选择正确的结果~
结合抛硬币的实验: 我们得到了一个样本 x = 正,为什么会产生这个数据,因为抛硬币有时候会得到正面,有时候会出现反面,”有时候”这个词对应的就是概率
第四个问题,我们描述抛硬币实验的问题时,可算到先验概率p(θ) = 3.99这样的数据,起初我还纳闷,概率不是一个0~1之间的小数吗,正面会有3.99这样的概率。
这又是惯性思维的一个反例,概率这东西其实是作用于离散变量上的一个名词,当θ为连续变量时,其实是不应该用 θ = 0.6 的概率这个说法来称呼的,翻概率论的书籍我们知道,连续随机变量在某一点处的概率其实是0的, p(θ) = 3.99更确切的解释应该是θ = 0.6处的概率密度为3.99。
所以下面才是连续变量形式的贝叶斯公式模型的正确形式:
$π(θ|x) = \frac{p(x|θ)π(θ)}{\int{p(x|θ)π(θ)d(θ)}}$
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------
路漫漫其修远兮,吾将上下而求索
posted on 2018-06-18 11:52 bingjianing 阅读(8660) 评论(4) 收藏 举报


 浙公网安备 33010602011771号
浙公网安备 33010602011771号