数据结构 --- 线段树

线段树是什么

线段树（Segment Tree）是一种基于分治思想的二叉树结构，用于在区间上进行信息统计，与按照二进制位（2的次幂）进行区间划分的树状数组相比，线段树是一种更通用的结构：

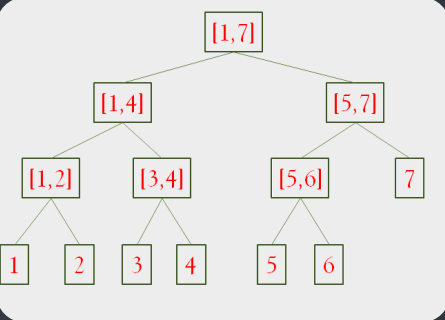
1. 线段树每一个节点都代表一个区间
2. 线段树具有唯一的根节点，代表的区间是整个统计范围，如[1,N]
3. 线段树的每一个叶节点都代表一个长度为1的元区间[x,x]
4. 对于每个内部节点[l,r],它的左子节点是[l,mid],右子节点是[mid + 1,r],其中mid = (l+r)/2（向下取整）

常用的五个操作：

1. 线段树的建树
2. 线段树的单点修改
3. 线段树的区间查询
4. pushup（通过子节点改父节点）、pushdown（通过父节点改子节点）

线段树的建树

1. 满二叉树->用一维数组
2. 编号为u，则父节点为u >> 1,左儿子为u << 1，右儿子为u << 1 | 1;

struct Node{
	int l,r;
	int v;//区间[l,r]中的最大值
}tr[N * 4];

void build(int u,int l,int r){
	tr[u] = {l,r};
	if(l == r) return ;
	int mid = l + r >> 1;
	build(u << 1,l,mid),build(u << 1 | 1,mid + 1,r);
}

线段树的区间查询

int query(int u,int l,int r){
	if(tr[u].l >= l && tr[u].r <= r) return tr[u].v;
	
	int mid = tr[u].l + tr[u].r >> 1;
	int v = 0;
	if(l <= mid) v = query(u << 1,l,r);
	if(r > mid) v = max(v,query(u << 1 | 1,l,r));
	
	return v;
}

线段树的单点修改

void modify(int u,int x,int v){
	if(tr[u].l == x && tr[u].r == x) tr[u].v = v;
	else{
		int mid = tr[u].l + tr[u].r >> 1;
		if(x <= mid) modify(u << 1,x,v);
		else modify(u << 1 | 1,x,v);
		pushup(u);
	}
}

由子节点的信息，来计算父节点的信息

void pushup(int u) //由子节点的信息，来计算父节点的信息
{
	tr[u].v = max(tr[u << 1].v,tr[u << 1 | 1].v);	
} 

由父节点的信息，来更新子节点的信息

void pushdown(int u){
	auto &root = tr[u],&left = tr[u << 1],&right = tr[u << 1 | 1];
	if(root.add){
		left.add += root.add,left.sum += (ll)(left.r - left.l + 1) * root.add;
		right.add += root.add,right.sum += (ll)(right.r - right.l + 1) * root.add;
		root.add = 0;
	}	
}

不用pushdown的综合应用：

void pushup(Node &u,Node &l,Node &r){
    u.sum = l.sum + r.sum;
    u.d = gcd(l.d,r.d);   
}
 
void pushup(int u){
    pushup(tr[u],tr[u << 1],tr[u << 1 | 1]);
}
 
void build(int u,int l,int r){
    if(l == r){
        ll b = w[r] - w[r - 1];
        tr[u] = {l,r,b,b};
    }else{
        tr[u] = {l,r};
        int mid = (l + r) >> 1;
        build(u << 1,l,mid);
        build(u << 1 | 1,mid + 1,r);
        pushup(u);
    }
}
 
void modify(int u,int x,ll v){
    if(tr[u].l == x && tr[u].r == x){
        ll b = tr[u].sum + v;
        tr[u] = {x,x,b,b};
    }else{
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(x <= mid) modify(u << 1,x,v);
        else modify(u << 1 | 1,x,v);
        pushup(u);
    }
}
 
Node query(int u,int l,int r){
    if(tr[u].l >= l && tr[u].r <= r) return tr[u];
    else{
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(r <= mid) return query(u << 1,l,r);
        else if(l > mid) return query(u << 1 | 1,l,r);
        else{
            auto left = query(u << 1,l,r);
            auto right = query(u << 1 | 1,l,r);
            Node res;
            pushup(res,left,right);
            return res;
        }
    }   
}

用pushdown的综合应用：

int n,m;
int w[N];

struct Node{
	int l,r;
	ll sum,add;
}tr[N << 2];

void pushup(int u){
	tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void pushdown(int u){
	auto &root = tr[u],&left = tr[u << 1],&right = tr[u << 1 | 1];
	if(root.add){
		left.add += root.add,left.sum += (ll)(left.r - left.l + 1) * root.add;
		right.add += root.add,right.sum += (ll)(right.r - right.l + 1) * root.add;
		root.add = 0;
	}	
}

void build(int u,int l,int r){
	if(l == r) tr[u] = {l,r,w[l],0};
	else{
		tr[u] = {l,r};
		int mid = (l + r) >> 1;
		build(u << 1,l,mid);
		build(u << 1 | 1,mid + 1,r);
		pushup(u);
	}
}

void modify(int u,int l,int r,int d){
	if(tr[u].l >= l && tr[u].r <= r){
		tr[u].sum += (ll)(tr[u].r - tr[u].l + 1) * d;
		tr[u].add += d;
	}else{		//一定要分裂 
		pushdown(u);
		int mid = (tr[u].l + tr[u].r) >> 1;
		if(l <= mid) modify(u << 1,l,r,d);
		if(r > mid) modify(u << 1 | 1,l,r,d);
		pushup(u);
	}	
}

ll query(int u,int l,int r){
	if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
	
	pushdown(u);
	int mid = (tr[u].l + tr[u].r) >> 1;
	ll sum = 0;
	if(l <= mid) sum = query(u << 1,l,r);
	if(r > mid) sum += query(u << 1 | 1,l,r);
	return sum; 	
}