单向链表

单向链表

前言

个人觉得，一开始接触数据结构看一大堆的定义对初学者并不友好，那样会令人望而生畏，一开始应该是简单的定义加上对代码的详细解释。

单向链表

单向链表是链表的一种，其特点是链表的连接方向是单向的，对链表的访问要通过头部开始，依序往下读取。

一个单向链表由多个节点组成，一个节点被分成两部分：

• 第一个部分是保存关于节点的信息，称作数据域。
• 第二个部分是存储下一个节点的地址，称作指针域。

单向链表结构示意图

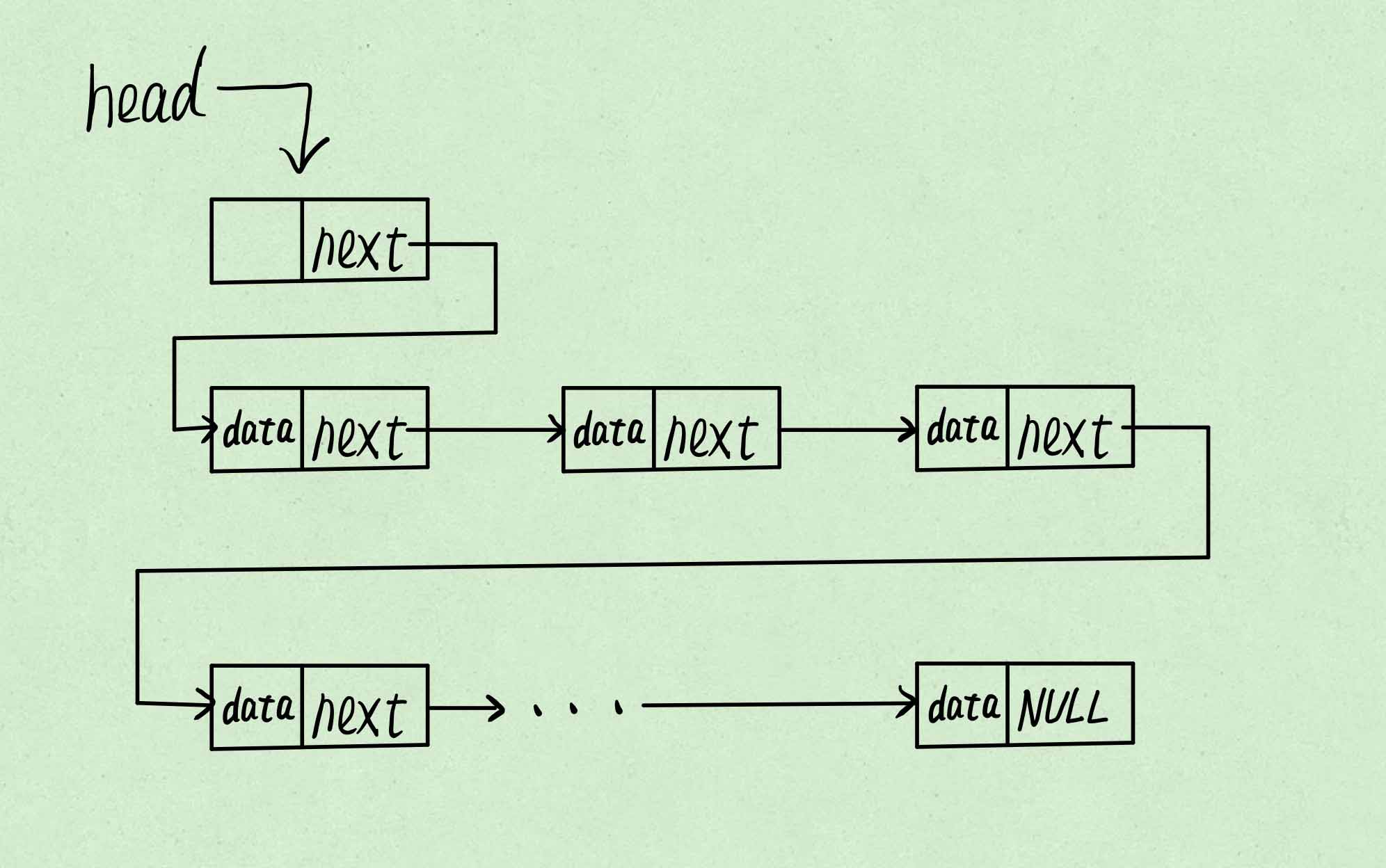
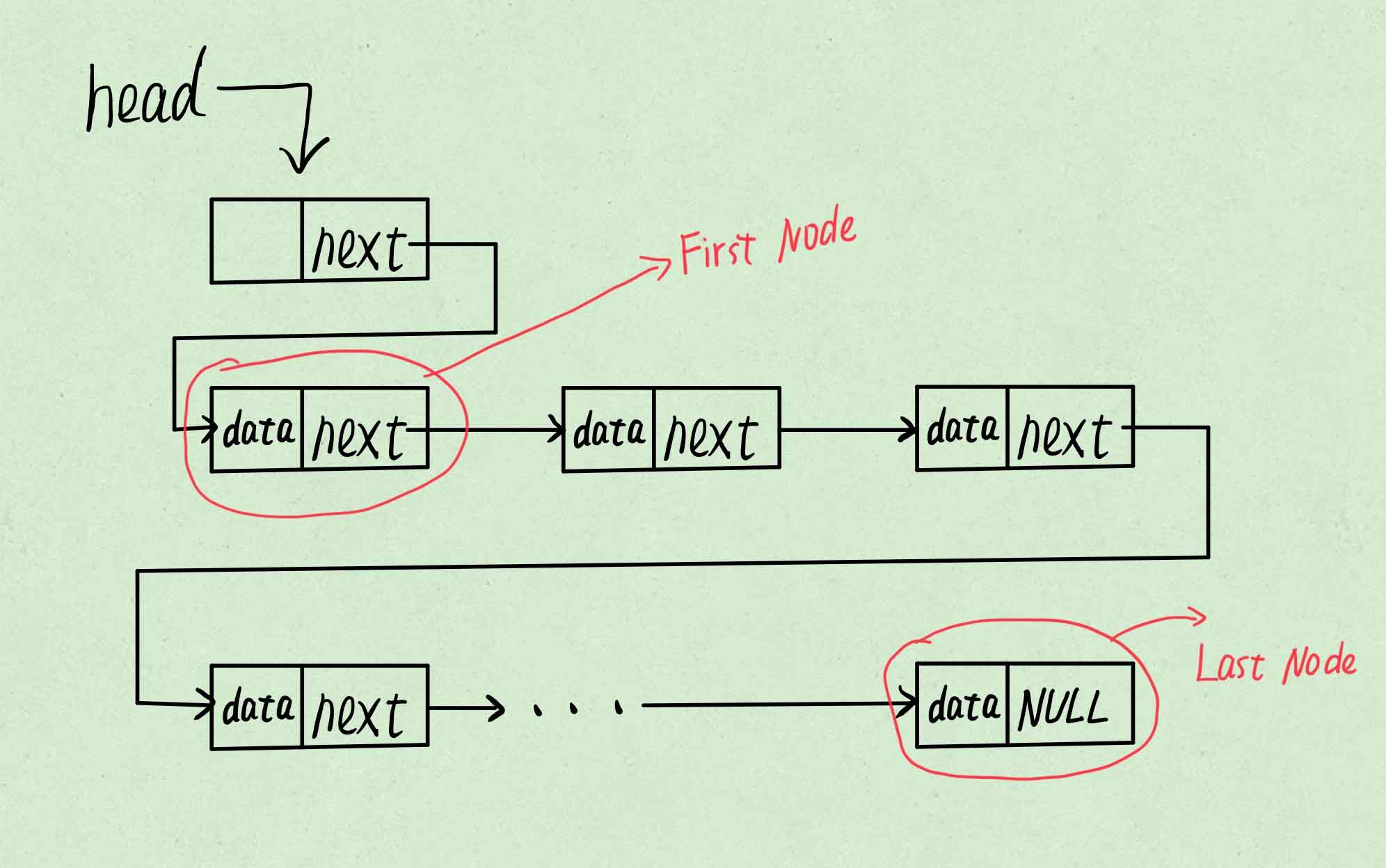
其中head是链表的头指针，指向的是表头节点，该节点的数据域无内容，其指针域指向的是链表的第一个节点。

链表最后一个节点的指针域为空，用NULL表示。

既不是表头结点也不是尾节点的节点数据域和指针域都不为空。

---

节点表示

struct node{
	int data;			// 数据域 
	struct node *next;	// 指针域 
}; 
typedef struct node Node;	 
typedef struct node* PNode;  // 节点指针 

其中data为节点保存的数据，next是节点指针类型的数据，用来保存下一个节点的地址。

---

链表初始化

链表初始化的内容是生成一个链表表头并返回其节点地址。如果初始化失败，则返回NULL表示初始化失败。

PNode Init(){
	
	PNode head = (PNode )malloc(sizeof(struct Node));
	if(!head)			// 申请内存空间失败的情况 
		return NULL;
	else{				// 申请成功的情况 
	 	head->next = NULL;			
		return head;
	} 
} 

---

数据的插入、删除、查找

插入

数据的增加操作即往链表中插入数据元素，往链表里插入元素有两种形式：

• 不要求次序的插入，使用头插法。
• 要求次序的精准插入，找到位置后插入。

---

不要求次序的插入

不要求次序的插入只需要将数据元素插入链表即可，因为单向链表只能从表头往后遍历，所以采用头插法减少插入的时间复杂度。

头插法

往链表里边插入元素的方法，可能你第一想到的是往链表的尾部直接添加元素，但是因为单向链表的特性，我们获得链表尾部的节点地址的时间复杂度是不稳定的。链表越长，获取链表尾部节点的地址就越慢。所以为了插入数据操作的高效性，我们使用头插法。

头插法，顾名思义就是直接在链表的头部插入数据。

大致操作如下：

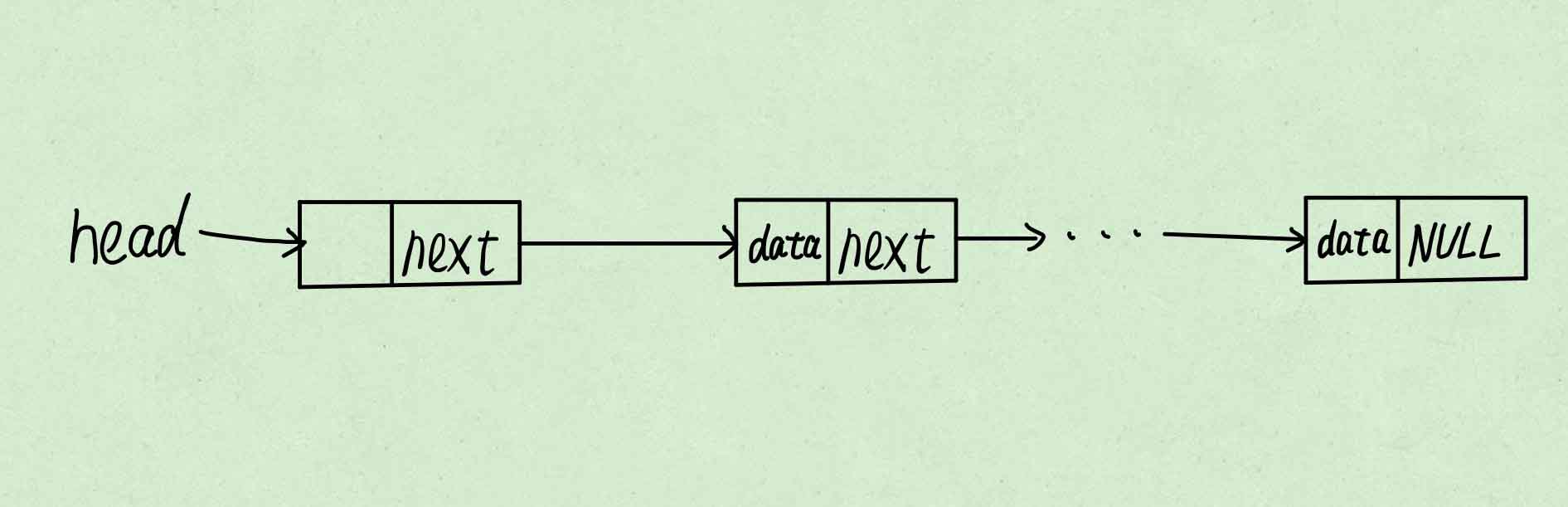
• 申请新节点

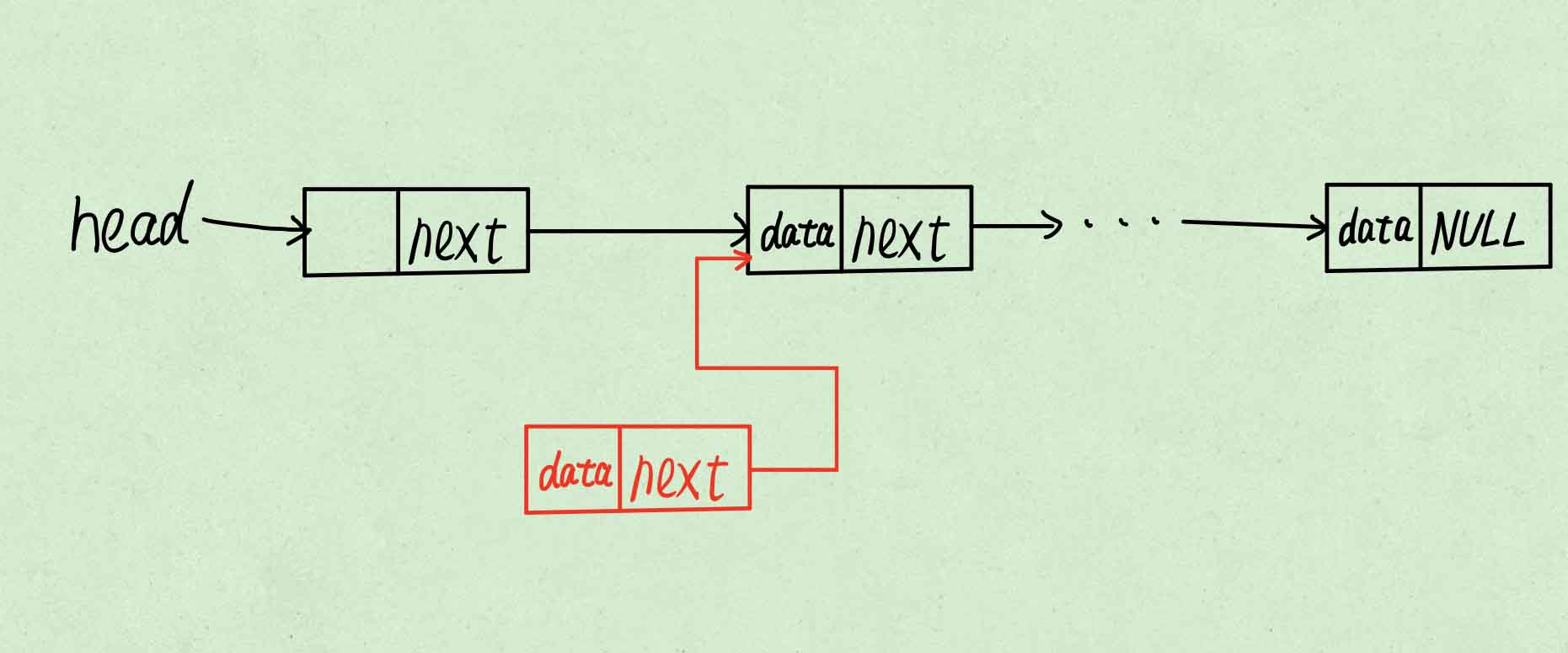
• 将需要插入的节点数据赋值给新节点数据域。

  

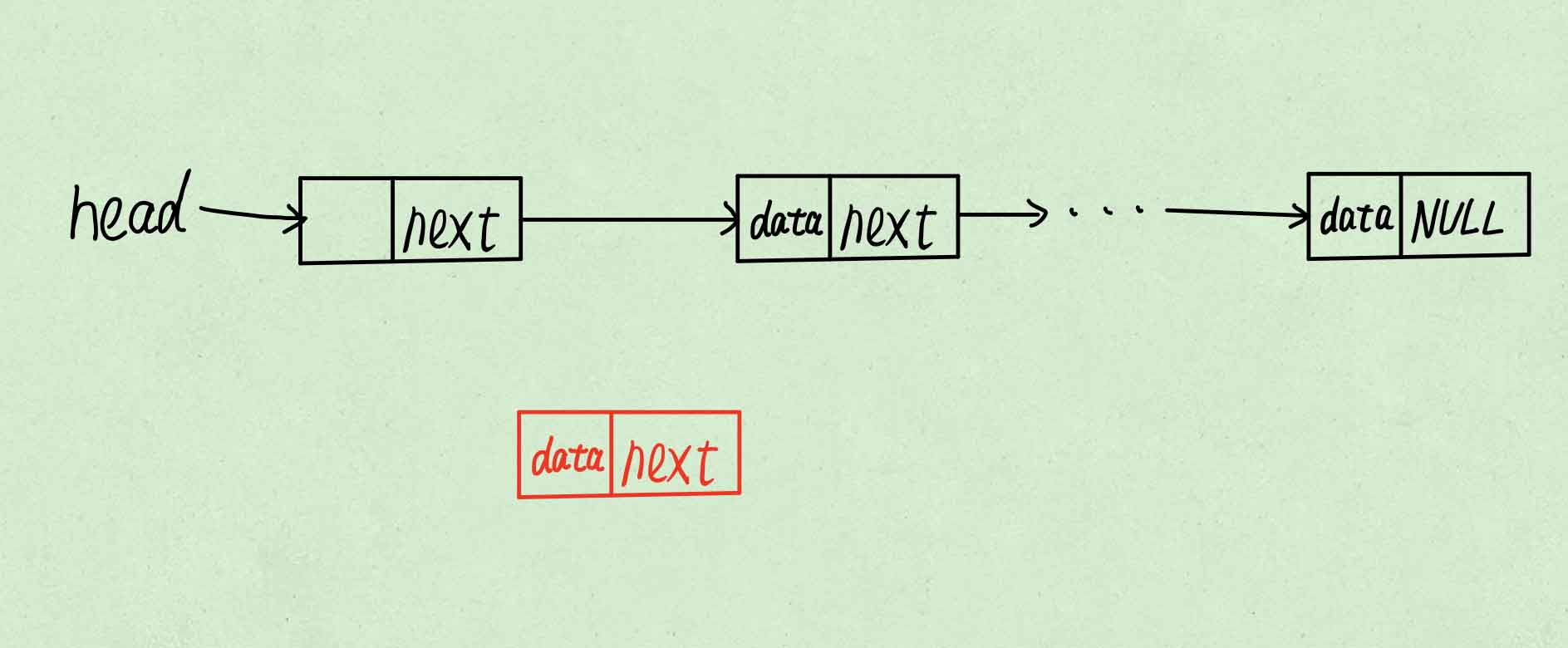
• 使新节点指向表头指向的节点。

  

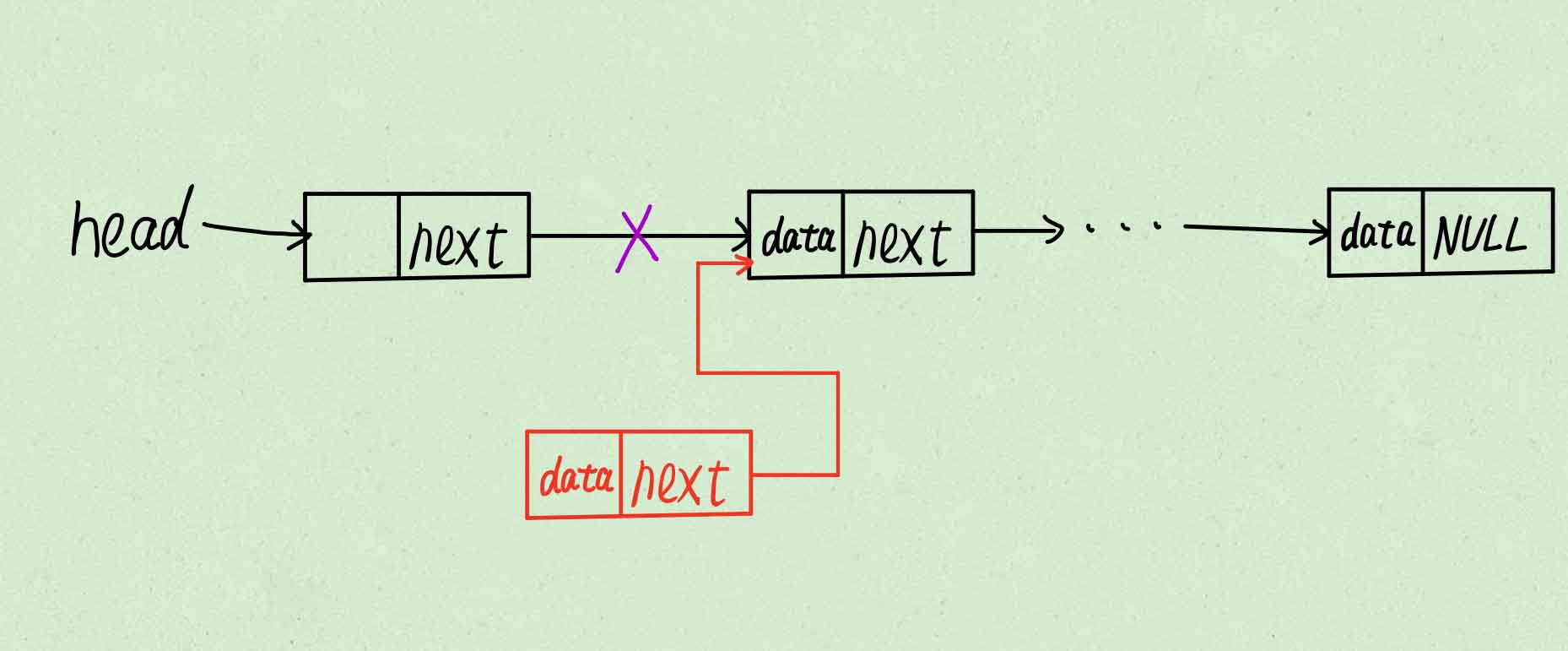
• 使表头指向新节点。

  

---

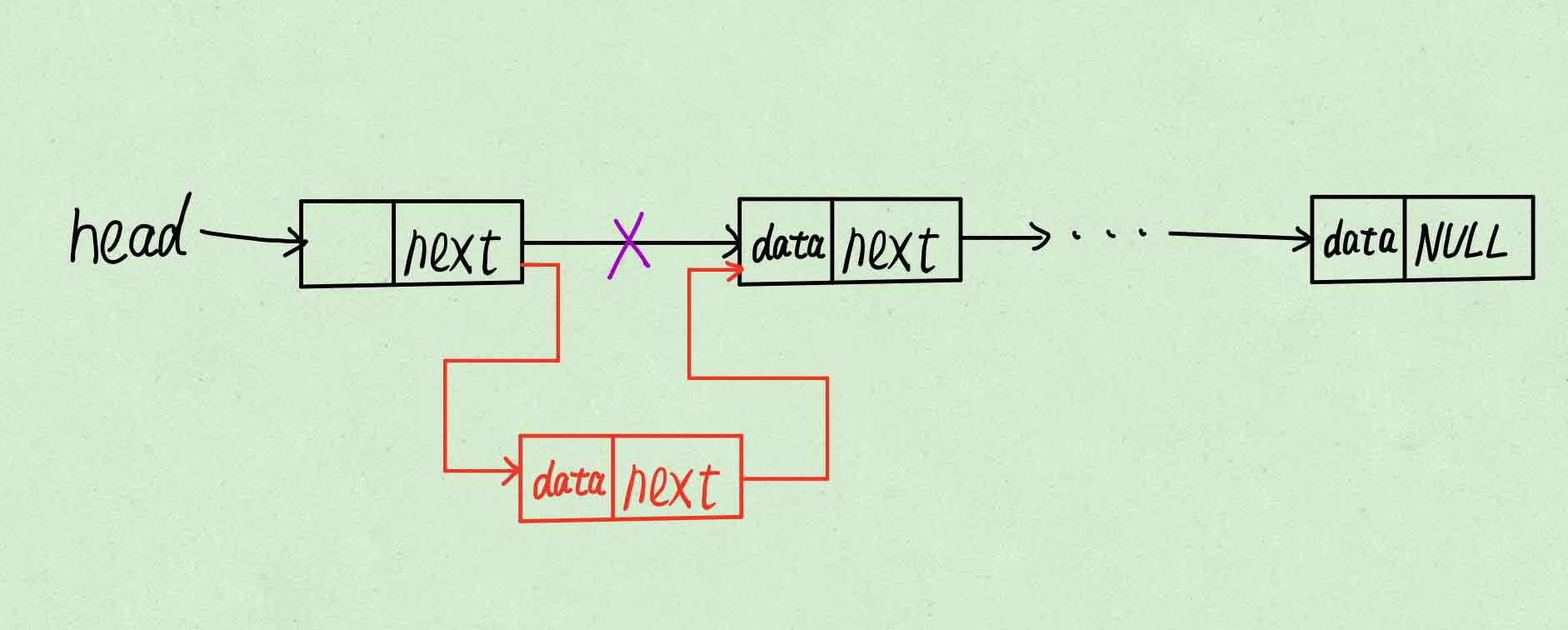
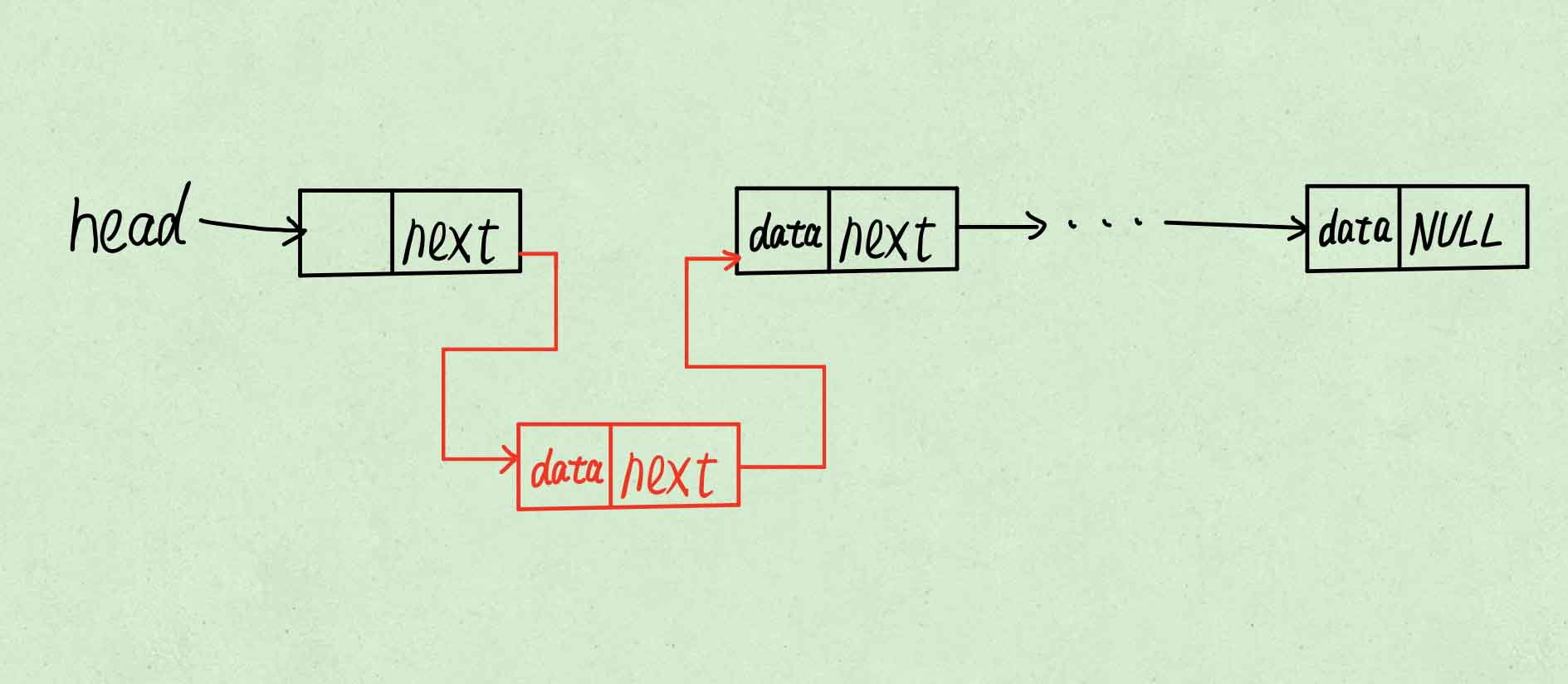
将该操作写成函数，该函数的作用是往链表插入元素，插入成功返回1，失败返回0。

代码为：

int Insert(PNode rt,int data){
	// 申请新节点的空间 
	PNode NewNode = (PNode )malloc(sizeof(struct Node));
	if(!NewNode)			// 申请失败的情况 
		return 0;
	else{					// 申请成功的情况
		NewNode->data = data;		// 节点数据赋值 
		NewNode->next = rt->next;	// 令新节点的next指向表头指向的节点 
		rt->next = NewNode;			// 令表头指向新节点 
		return 1;
	} 
}

---

精准位置插入

将数据元素插入到第i个元素之后，如果i超过链表长度则将其插入到链表的最后位置。插入成功返回1，失败返回0。

int Insert_i(PNode rt,int i,int data){
	// 申请新节点空间
	PNode NewNode = (PNode )malloc(sizeof(struct Node));
	if(!NewNode)					// 申请空间失败的情况 
		return false; 
	else{							// 申请成功的情况 
		NewNode->data = data;		// 节点数据赋值 
		int index = 0;
		PNode pr = rt;				// pr的代表的是第i个节点的地址 
		while(pr->next != NULL){	//这个循环的作用是使pr获取第i个节点的地址 
			index++;
			pr = pr->next;
			if(index == i)break;
		}
		NewNode->next = pr->next;	//获取地址之后进行修改，类似于头插法的方式 
		pr->next = NewNode;
		return 1;
	}
} 

---

删除

删除操作是插入操作的逆操作，有两种形式：

• 删除特定元素。
• 删除特定位置的元素。

删除特定元素

找到该元素的地址和其前驱即可对该元素进行删除，删除成功返回1，失败返回0。

int Delete(PNode rt,int data){
	PNode pre = rt,add = rt;
    // 查找链表中是否含有此元素
	while(add->next != NULL){
		pre = add;
		add = add->next;
		if(add->data == data)break;
	}
	if(add->data != data || add == rt)return 0; // 未找到的情况
	else{										// 找到的情况
		pre->next = add->next;			// 直接让前驱指向第i个元素的后继
		free(add);						// 释放该节点空间
		return 1;
	}
} 

---

删除特定位置的元素

删除第i个位置的元素，如果i大于链表长度则删除失败返回0，成功则返回1。

int Delete_i(PNode rt,int i){
	PNode pre = rt,add = rt;
	int index = 0;
	while(add->next != NULL){
		index++;
		pre = add;
		add = add->next;
		if(index == i)break;		// 找到第i个元素
	}
	if(index != i)return 0;			//i大于链表长度或者i<= 0的情况
	else{
		pre->next = add->next;		// 直接让前驱指向第i个元素的后继
		free(add);					// 释放第i个节点
		return 1;					// 删除成功
	}
}

---

查找

查找操作即在链表中查找是否存在某元素，若存在返回其节点地址，不存在返回NULL。

PNode find(PNode rt,int data){
	PNode pr = rt;
	while(pr->next != NULL){
		pr = pr->next;
		if(pr->data == data)break;	// 找到的情况
	}
	if(pr->data != data || pr == rt)return NULL;	// 未找到或者链表为空的情况
	else return pr;
}

这篇文章主要介绍了单向链表中最重要的三类操作，分别是数据插入、数据删除、数据查找。

实际上还有很多其他的操作，初学阶段能学会这几种足够了，贪多嚼不烂。

一下是测试函数正确性的源代码：

#include<stdio.h>
#include<stdlib.h>

struct node{
	
	int data;			// 数据域 
	struct node *next;	// 指针域 
	
}; 

typedef struct node Node;	 // 对结构体重命名，方便定义数据
typedef struct node* PNode;  // 节点指针 

PNode Init(){
	
	PNode head = (PNode )malloc(sizeof(Node));
	if(!head)			// 申请内存空间失败的情况 
		return NULL;
	else{				// 申请成功的情况 
	 	head->next = NULL;			
		return head;
	} 
} 

int Insert(PNode rt,int data){
	// 申请新节点的空间 
	PNode NewNode = (PNode )malloc(sizeof(Node));
	if(!NewNode)			// 申请失败的情况 
		return 0;
	else{					// 申请成功的情况
		NewNode->data = data;		// 节点数据赋值 
		NewNode->next = rt->next;	// 令新节点的next指向表头指向的节点 
		rt->next = NewNode;			// 令表头指向新节点 
		return 1;
	} 
}

int Insert_i(PNode rt,int i,int data){
	// 申请新节点空间
	PNode NewNode = (PNode )malloc(sizeof(Node));
	if(!NewNode)					// 申请空间失败的情况 
		return 0; 
	else{							// 申请成功的情况 
		NewNode->data = data;		// 节点数据赋值 
		int index = 0;
		PNode pr = rt;				// pr的代表的是第i个节点的地址 
		while(pr->next != NULL){	//这个循环的作用是使pr获取第i个节点的地址 
			index++;
			pr = pr->next;
			if(index == i)break;
		}
		NewNode->next = pr->next;	//获取地址之后进行修改，类似于头插法的方式 
		pr->next = NewNode;
		return 1;
	}
} 

int Delete(PNode rt,int data){
	PNode pre = rt,add = rt;
    // 查找链表中是否含有此元素
	while(add->next != NULL){
		pre = add;
		add = add->next;
		if(add->data == data)break;
	}
	if(add->data != data || add == rt)return 0; // 未找到的情况
	else{										// 找到的情况
		pre->next = add->next;			// 直接让前驱指向第i个元素的后继
		free(add);						// 释放该节点空间
		return 1;
	}
} 

int Delete_i(PNode rt,int i){
	PNode pre = rt,add = rt;
	int index = 0;
	while(add->next != NULL){
		index++;
		pre = add;
		add = add->next;
		if(index == i)break;		// 找到第i个元素
	}
	if(index != i)return 0;			//i大于链表长度或者i<= 0的情况
	else{
		pre->next = add->next;		// 直接让前驱指向第i个元素的后继
		free(add);					// 释放第i个节点
		return 1;					// 删除成功
	}
}

PNode find(PNode rt,int data){
	PNode pr = rt;
	while(pr->next != NULL){
		pr = pr->next;
		if(pr->data == data)break;	// 找到的情况
	}
	if(pr->data != data || pr == rt)return NULL;	// 未找到或者链表为空的情况
	else return pr;
}

// 遍历输出链表全部元素 
void Tra(PNode rt){
	PNode pr = rt;
	while(pr->next != NULL){
		pr = pr->next;
		printf("%d ",pr->data);
	}
	printf("\n");
}

int main(){
	
	PNode L1,L2;
	// 初始化两个链表 
	L1 = Init();
	L2 = Init();
	if(L1)printf("链表一创建成功。\n");
	if(L2)printf("链表二创建成功。\n");
	
	int i ;
	printf("L1使用头插法插入1~10:\n");
	for(i = 1; i <= 10; i++)
		Insert(L1,i);
	Tra(L1);
	printf("L2使用位置插入10~19:\n");
	for(i = 10; i <= 19; i++)
		Insert_i(L2,i-9,i);
	Tra(L2);
	
	printf("删除L1元素1、2、3、4、5：\n");
	for(i = 1; i <= 5; i++)
		Delete(L1,i);
	Tra(L1);
	printf("删除L2第10个元素：\n");
	Delete_i(L2,10);
	Tra(L2);
	return 0;
}

输出为：

链表一创建成功。
链表二创建成功。
L1使用头插法插入1~10:
10 9 8 7 6 5 4 3 2 1
L2使用位置插入10~19:
10 11 12 13 14 15 16 17 18 19
删除L1元素1、2、3、4、5：
10 9 8 7 6
删除L2第10个元素：
10 11 12 13 14 15 16 17 18