快速傅里叶变换的迭代法代码实现

在上文中，我们聊到了离散傅里叶变换的实现，其时间复杂度是O(N^2)，以及快速傅里叶变换的递归实现，其时间复杂度是O(NlogN)。

但是因为实现方式是用递归法，并且为了分离奇偶下标的数据，又重新申请了一些数组，所以空间复杂度有所上升，显然不是最优解。分离奇偶下标的过程：

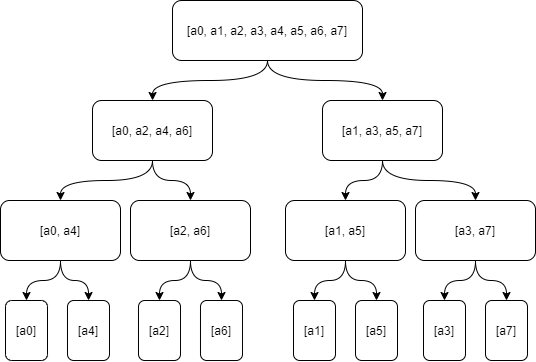
递归法是从最顶端开始，一层一层循环，不断地拆分数组，到最底端。然后再一层层地做特殊运算，回到最顶端。

蝴蝶操作

上述这个特殊运算的操作叫做蝴蝶（butterfly）操作：

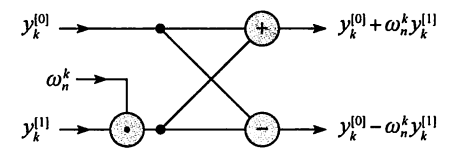
图自《算法导论》

如上，譬如输入两个数 y[0]和y[1]，经过一阵你中有我，我中有你的X型运算之后，输出的依然是两个数。

至于为什么叫蝴蝶运算，可能是这个叉叉的X型的形状比较像蝴蝶吧：

继续刚才我们说到的再一层层地做蝴蝶运算，回到最顶端的过程，如下图：

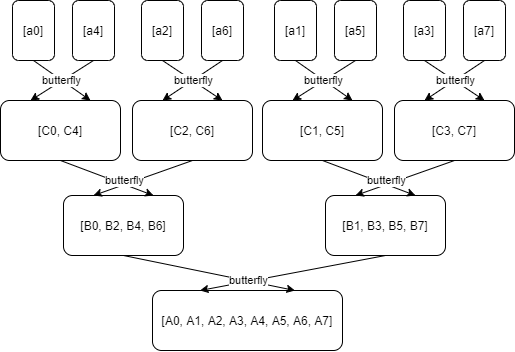
下图展现了和上图相同的意思，但是更加精确：

以上，我们发现有趣的一点：

[a0, a4, a2, a6, a1, a5, a3, a7] 这个数组转换成结果 [A0, A1, A2, A3, A4, A5, A6, A7]。

这个计算的过程是可以原地进行的，这样的话空间复杂度可以做到O(1)（几乎不不需要额外的内存空间）。

位逆序(bit reverse)

为了达到这样的效果，我们首先需要做的是：

其中规律已经有人研究出来了：位逆序 bit reverse这个规律，对于任何二次幂减一的数都管用。本文图中仅以最大值7作为示例。

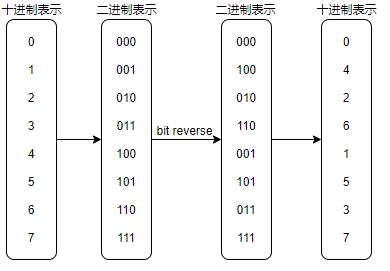
说道bit reverse，显然这是一道leetcode题啊，参见leetcode第190题。

https://leetcode-cn.com/problems/reverse-bits/

点赞数最高的那个答案写得更容易理解一点，于是直接拿来用下。不过因为我们的bits位数会有变化，不仅仅是32bits，也可能是8 bits或者是128 bits，所以稍加修改即可：

uint64_t reverseBits(uint64_t n, uint64_t bits) {
    uint64_t res = 0;
    for (uint64_t i = 0; i < bits; ++i) {
        res = (res << 1) | (n & 1);
        n >>= 1;
    }
    return res;
}

然后在arrayReorder中调用 reverseBits 对原数组中的数据进行调换：

void arrayReorder(vector<complex <double>> &data)
{
    uint64_t x, r = log2(data.size());
    for(uint64_t i = 0; i < data.size(); ++i){
        x = reverseBits(i, r);
        if (x > i){
            swap(data[i], data[x]);
        }
    }
}

接着为我们就可以层层循环地进行FFT操作了，以下是我基于《算法导论》中的伪代码，重写得C++代码(亲测可用)：

#include <stdio.h>
#include <stdlib.h>
#include <cstdint>
#include <iostream>
#include <complex>
#include <vector>
#include <cmath>
#include <algorithm>

using namespace std;
const double pi = acos(-1.0);

void fft_iter(vector<complex<double>>& data, bool inv)
{
    complex<double> wn, deltawn, t, u;
    uint64_t length = data.size();
    uint64_t log2n = (length==0)?0:log2(length);
    int64_t sign = inv?1:-1;

    arrayReorder(data);
    
    for (uint64_t i = 1; i <= log2n; ++i) //logn 次循环
    {
        uint64_t m = 1<<i; 
        deltawn = polar<double>(1, sign*2*pi/m);
        for (uint64_t k = 0; k < length; k += m) //这个for和下面的for加起来，是n次循环
        {
            wn = polar<double>(1, 0);
            for (uint64_t j = 0; j < m/2; j++)
            {
                t = data[k + j + m/2]*(wn);
                u = data[k + j];
                data[k + j] = u + t;
                data[k + j + m/2]= u - t;
                wn *= deltawn;
            }
        }
    }
    if (inv)
        for (uint64_t i = 0; i < length; ++i)
            data[i] /= length;
}

如果有对不同循环中的ω的值不一样有所疑问，可以参考上一篇文章哈。

以上代码，会发现时间复杂度依然是O(NlogN)，但是空间复杂度是恒定的O(1)。在此，迭代法相较递归法又上升了一个台阶，不得不感叹算法的魔力。

对了，有傅里叶正变换，就有傅里叶逆变换，其区别就如离散傅里叶变换和离散傅里叶逆变换的公式区别:

离散傅里叶正变换：

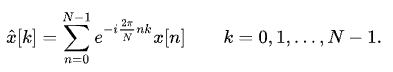
离散傅里叶逆变换：

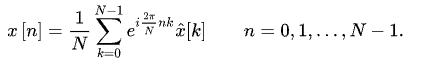
在上述代码中，快速傅里叶正变换（时域转换成频域）：

fft_iter(data, false);

快速傅里叶逆变换（频域转换成时域）：

fft_iter(data, true);

本文中介绍的FFT算法，只针对序列长度为2次幂的DFT计算，即基2-FFT。并且本文介绍的只是FFT算法中的一种，即时域抽取dit（Decimation-in-time），加上是基2-FFT，所以该算法简称为DIT2。

这一系列说到现在，到底是谁让傅里叶变换变快了的呢？FFT的基本思路是在1965年由J. W. Cooley和J. W. Tukey合作发表An algorithm for the machine calculation of complex Fourier series之后开始为人所知的。

DIT和DIF

在FFT算法中，针对输入做不同方式的分组会造成输出顺序上的不同。如果我们使用时域抽取（Decimation-in-time），那么输入的顺序将会是比特反转排列（bit-reversed order），输出将会依序排列。但若我们采取的是频域抽取（Decimation-in-frequency），那么输出与输出顺序的情况将会完全相反，变为依序排列的输入与比特反转排列的输出。