Java数据结构和算法（七）B+ 树

Java数据结构和算法（七）B+ 树

数据结构与算法目录(https://www.cnblogs.com/binarylei/p/10115867.html)

我们都知道二叉查找树的查找的时间复杂度是 O(logN)，其查找效率已经足够高了，那为什么还有 B 树和 B+ 树的出现呢？难道它两的时间复杂度比二叉查找树还小吗？答案当然不是， B 树和 B+ 树的出现是因为另外一个问题，那就是磁盘 IO。

一、计算机中数据的存储原理

页是计算机管理存储的逻辑块，硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块。每个块都称为一页(在许多操作系统中，页大小通常为 4K)，主存和磁盘以页为单位交换数据。

文件系统及数据库系统的设计利用了磁盘预读原理，将一个节点的大小设计为一个页，这样每个节点只需要一次 IO 就可以完全载入。

众所周知，IO 操作的效率很低，那么，当在大量数据存储中，查询时我们不能一下子将所有数据加载到内存中，只能逐一加载磁盘页，每个磁盘页对应树的节点。造成大量磁盘 IO 操作（最坏情况下为树的高度）。平衡二叉树由于树深度过大而造成磁盘 IO 读写过于频繁，进而导致效率低下。

所以，我们为了减少磁盘 IO 的次数，就你必须降低树的深度，将“瘦高”的树变得“矮胖”。一个基本的想法就是：

• 每个节点存储多个元素
• 摒弃二叉树结构，采用多叉树

这样就引出来了一个新的查找树结构 - 多路查找树。 根据 AVL 给我们的启发，一颗平衡多路查找树(B~树)自然可以使得数据的查找效率保证在 O(logN) 这样的对数级别上。

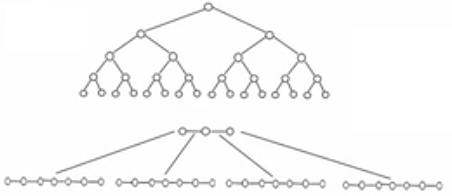
下面来具体介绍一下 B 树（Balance Tree），

二、B 树

一个 m 阶的 B 树具有如下几个特征：B 树中所有结点的孩子结点最大值称为 B 树的阶，通常用 m 表示。一个结点有 k 个孩子时，必有 k-1 个关键字才能将子树中所有关键字划分为 k 个子集。

2.1 特点

1. 根结点至少有两个子女。
2. 每个中间节点都包含 k-1个 元素和 k 个孩子，其中 ceil（m/2） ≤ k ≤ m
3. 每一个叶子节点都包含 k-1 个元素，其中 ceil（m/2） ≤ k ≤ m
4. 所有的叶子结点都位于同一层。
5. 每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分
6. 每个结点的结构为：（n，A0，K1，A1，K2，A2，… ，Kn，An）
   其中，Ki(1≤i≤n) 为关键字，且 Ki < Ki + 1 (1 ≤ i ≤n-1)。
   Ai(0 ≤ i ≤ n)为指向子树根结点的指针。且 Ai 所指子树所有结点中的关键字均小于 Ki + 1。
   n 为结点中关键字的个数，满足 ceil(m / 2) - 1≤ n ≤m - 1。

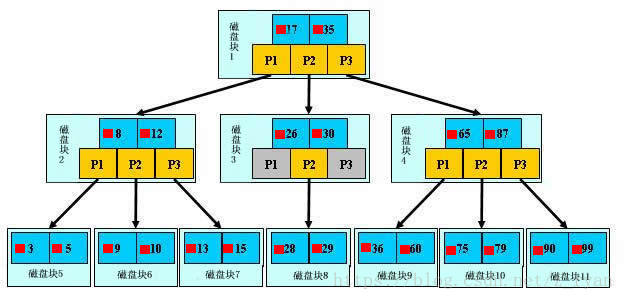
示例：三阶 B 树

2.1 查询

以上图为例：若查询的数值为５：

第一次磁盘ＩＯ：在内存中定位（与17、35比较），比17小，左子树；
第二次磁盘ＩＯ：在内存中定位（与８、12比较），比８小，左子树；
第三次磁盘ＩＯ：在内存中定位（与3、5比较），找到5，终止。

整个过程中，我们可以看出：比较的次数并不比二叉查找树少，尤其适当某一节点中的数据很多时，但是磁盘 IO 的次数却是大大减少。比较是在内存中进行的，相比于磁盘 IO 的速度，比较的耗时几乎可以忽略。所以当树的高度足够低的话，就可以极大的提高效率。相比之下，节点中的元素多点也没关系，仅仅是多了几次内存交互而已，只要不超过磁盘页的大小即可。

注意：

1. B 树主要用于文件系统以及部分数据库索引，如 MongoDB。而大部分关系数据库则使用 B+ 树做索引，例如：mysql 数据库；
2. 从查找效率考虑一般要求 B 树的阶数 m >= 3;
3. B 树上算法的执行时间主要由读、写磁盘的次数来决定，故一次 I/O 操作应读写尽可能多的信息。因此 B- 树的结点规模一般以一个磁盘页为单位。一个结点包含的关键字及其孩子个数取决于磁盘页的大小。

三、B+ 树

B+ 树是 B 树的变种，有着比 B 树更高的查询效率。下面，我们就来看看 B+ 树和 B 树有什么不同

3.1 特点

1. 有 k 个子树的中间节点包含有 k 个元素（B 树中是 k-1 个元素），每个元素不保存数据，只用来索引，所有数据
   都保存在叶子节点。

2. 所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小
   自小而大顺序链接。

3. 所有的中间节点元素都同时存在于子节点，在子节点元素中是最大（或最小）元素。

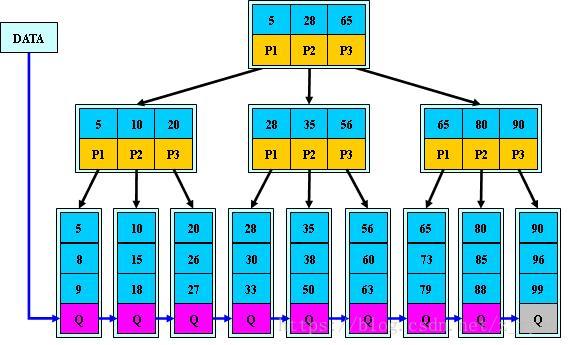
下面是一棵 3 阶的 B+ 树：

B+ 树通常有两个指针，一个指向根结点，另一个指向关键字最小的叶子结点。因些，对于 B+ 树进行查找两种运算：一种是从最小关键字起顺序查找，另一种是从根结点开始，进行随机查找。

3.2 查找

B+ 树的优势在于查找效率上 ，下面我们做一具体说明：

首先，Ｂ＋树的查找和Ｂ树一样，类似于二叉查找树。起始于根节点，自顶向下遍历树，选择其分离值在要查找值的任意一边的子指针。在节点内部典型的使用是二分查找来确定这个位置。

（1）不同的是，Ｂ＋树中间节点没有卫星数据（索引元素所指向的数据记录），只有索引，而Ｂ树每个结点中的每个关键字都有卫星数据；这就意味着同样的大小的磁盘页可以容纳更多节点元素，在相同的数据量下，Ｂ＋树更加“矮胖”，ＩＯ操作更少

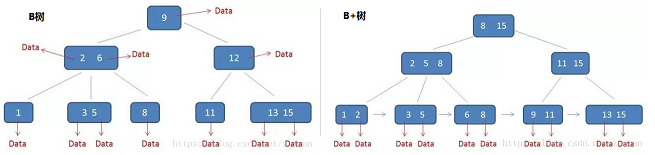
（2）其次，因为数据结构的不同，导致查询过程也不同；B 树的查找只需找到匹配元素即可，最好情况下查找到根节点，最坏情况下查找到叶子结点，所说性能很不稳定，而 B+ 树每次必须查找到叶子结点，性能稳定

（3）在范围查询方面，B+ 树的优势更加明显

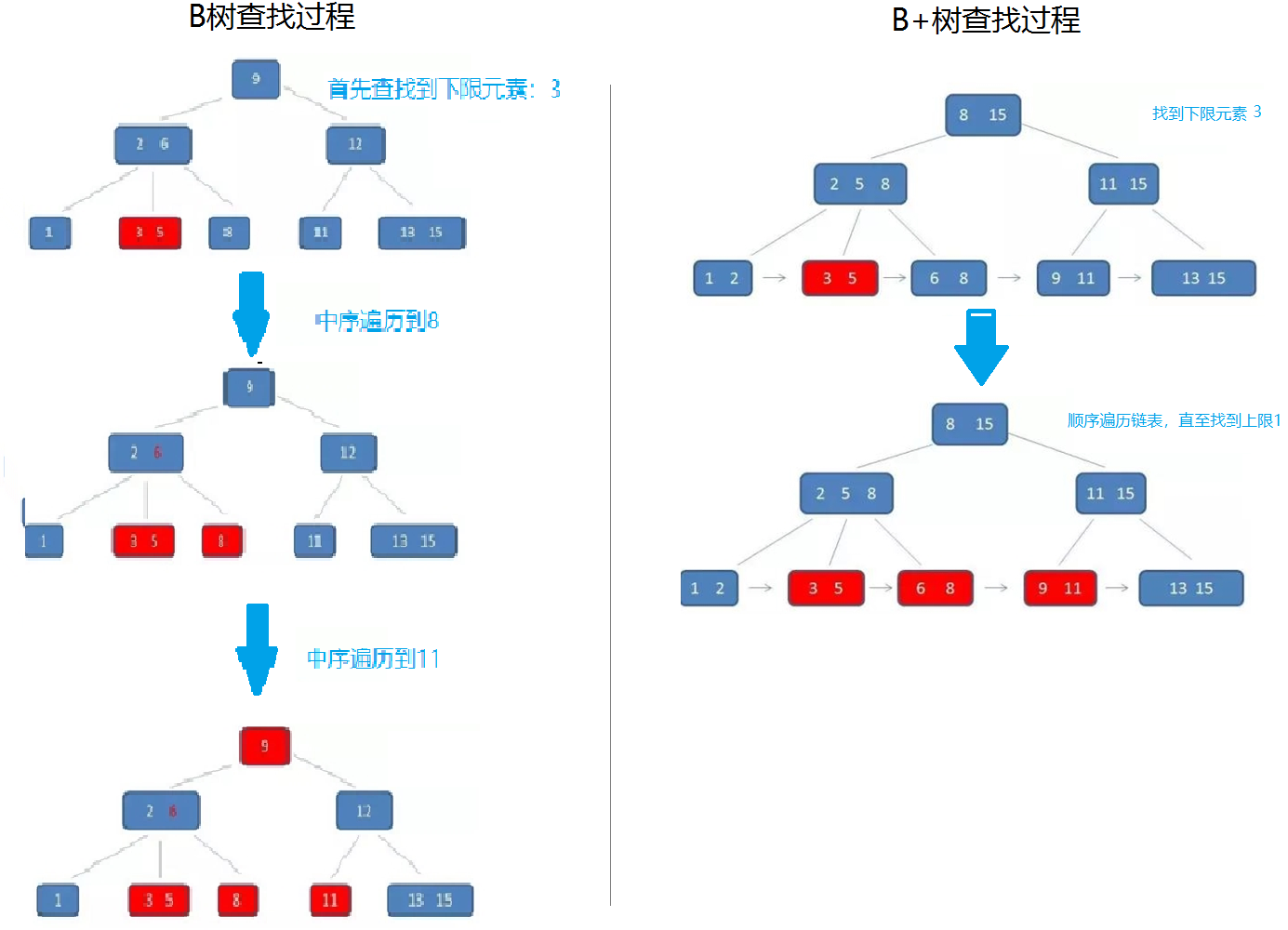
B树的范围查找需要不断依赖中序遍历。首先二分查找到范围下限，在不断通过中序遍历，知道查找到范围的上限即可。整个过程比较耗时。

而 B+ 树的范围查找则简单了许多。首先通过二分查找，找到范围下限，然后同过叶子结点的链表顺序遍历，直至找到上限即可，整个过程简单许多，效率也比较高。

例如：同样查找范围 [3-11]，两者的查询过程如下：

四、总结

B+ 树相比 B 树的优势：

1. 单一节点存储更多的元素，使得查询的 IO 次数更少；
2. 所有查询都要查找到叶子节点，查询性能稳定；
3. 所有叶子节点形成有序链表，便于范围查询。

参考：

1. 《简单剖析B树（B-Tree）与Ｂ+树》：https://blog.csdn.net/z_ryan/article/details/79685072

---

每天用心记录一点点。内容也许不重要，但习惯很重要！