Java 数据结构 - 堆和堆排序：为什么快排比堆排序性能好 - binarylei

Java 数据结构 - 堆和堆排序：为什么快排比堆排序性能好

Java 数据结构 - 堆和堆排序：为什么快排比堆排序性能好

数据结构与算法目录(https://www.cnblogs.com/binarylei/p/10115867.html)

关于二叉树这种数据结构在实现软件工程中的应用，前面我们已经介绍了红黑树，下面我们再介绍另一种常见的二叉树 - 堆。

红黑树：基于平衡二叉查找树的动态数据结构，用于快速插入和查找数据，其时间复杂度都是 O(logn)。
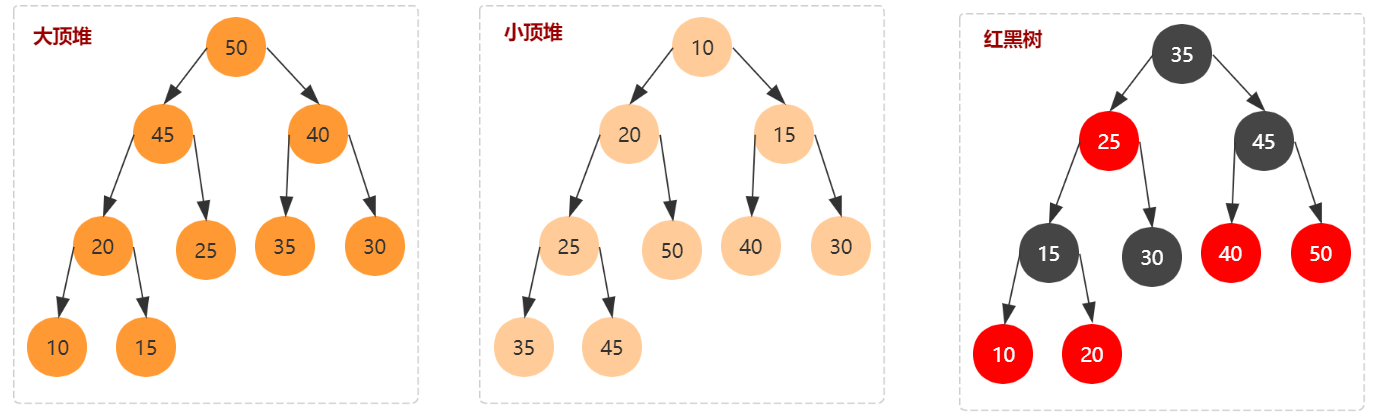
堆：按照结点大于等于（或小于等于）子结点，又分为大顶堆和小顶堆。和红黑树不同，椎只是部分有序，即 "左结点 < 父结点 && 右结点 < 父结点"，而有序二叉树要求 "左结点 < 父结点 < 右结点"。椎插入和删除元素的时间复杂度都是 O(logn)。堆常见的应用有优先级队列和堆排序。

1. 什么是堆

1.1 堆的定义

堆的严格定义如下，只要满足这两点，它就是一个堆：

堆是一个完全二叉树；
堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。

说明： 和红黑树不同，椎并是一个部分有序队列，尤其要注意以下两点。

堆是完全二叉树，因此堆这种数据都是用数组进行存储。
对于每个节点的值都大于等于子树中每个节点值的堆，叫作大顶堆。反之则是小顶堆。

1.2 堆的常见操作

堆的常见操作两个，分别是插入元素和删除堆顶元素：

堆化(heapify)：往堆中插入元素叫做堆化。堆化分为从下往上和从上往下两种堆化方法。
删除堆顶元素：我们知道，堆顶元素是最小或最大元素。删除堆顶元素后，需要通过从上往下的堆化，使其重新满足堆的定义。

（1）堆化

我们往一个小顶堆中添加新的结点，分析从下往上是如何进行堆化。当然，你也可以使用从下往上的堆化。

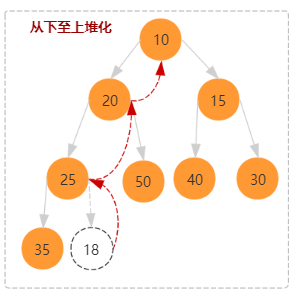
如上图所示，插入结点时从下往上是堆化为两步：

将数组最后位置添加一个新的结点，也就是 arr[size] = value。
从这个新结点和父结点依次向上比较并交换，直接重新符合堆的定义。其时间复杂度为树的高度，也就是 O(logn)。

private int[] arr;
private int size;

// arr[0] 不存储任何元素，当然你也可以将堆整体向前移动一位
public void add(int value) {
    if (size >= capcity) return;
    ++size;
    arr[size] = value;
    int i = size;
    while (i > 0 && arr[i / 2] > arr[i]) {
        swap(arr, i, i / 2);
        i = i / 2;
    }
}

（2）删除堆顶元素

与插入结点时相反，删除元素时需要从上至下堆化

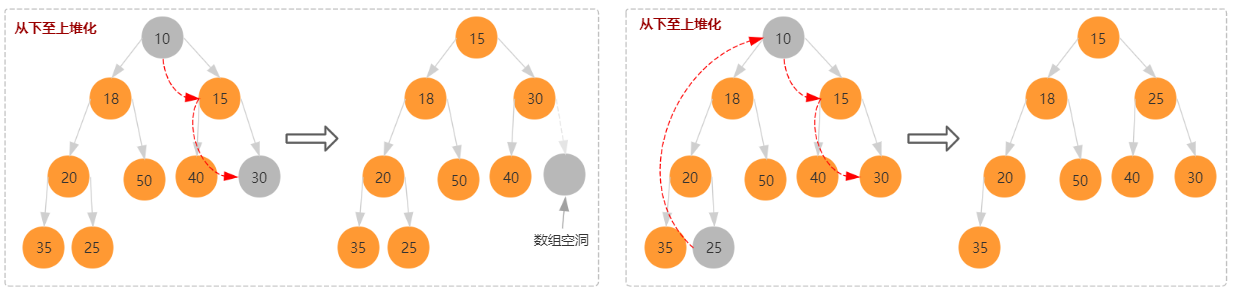
需要注意的是直接和子结点比较并交换位置，可能会出现数组空洞，不符合完全二叉树的定义，如右图所示出现的数据空洞。解决方案如左所示，先将数组最后一位的结点交换到堆顶，然后再从上至下比较交换。

将数组最后结点赋值给椎顶结点，也就是 arr[1] = arr[size]。
从这个新结点和子结点依次向下比较并交换，直接重新符合堆的定义。其时间复杂度为树的高度，也就是 O(logn)。

public int poll() {
    if (size <= 0) return -1;
    int value = arr[1];
    int i = 1;
    arr[i] = arr[size];
    arr[size] = 0;
    size--;

    while (true) {
        int minPos = i;
        if (size >= 2 * i && arr[minPos] > arr[2 * i]) minPos = 2 * i;
        if (size >= 2 * i + 1 && arr[minPos] > arr[2 * i + 1]) minPos = 2 * i + 1;
        if (minPos == i) break;

        swap(arr, i, minPos);
        i = minPos;
    }
    return value;
}

2. 堆排序

如果我们要堆数据结构实现从小到大的排序，该怎么实现呢？我们知道将数组堆化成大顶堆后，堆顶是最大值，然后我们依次取出堆顶元素，这样取出的元素就是按从大到小的顺序，我们每次取出元素时依次放到数组最后。这样当全部取出后，就实现了从小到大的排序。堆排序分为两步：

堆化：将数组原地建成一个堆。
排序：依次取出堆顶元素与数组最后一个元素交换位置。

2.1 堆化

原地堆化也有两种思路：

从下往上进行堆化。和插入排序一样，将数组分为两部为：已经堆化和未堆化。依次遍历未堆化部为，将其插入到已经堆化部分。
从上往下进行堆化。遍历所有的叶子结点，将其与堆顶结点交换后从上往下进行堆化。

// 从下往上堆化
private static void heavify(Integer[] arr) {
    for (int i = 1; i < arr.length; i++) {
        shiftUp(i, arr);
    }
}
// 大顶堆：从下往上堆化
private static void shiftUp(int i, Integer[] arr) {
    while (i > 0 && arr[i] > arr[(i - 1) / 2]) {
        swap(arr, i, (i - 1) / 2);
        i = (i - 1) / 2;
    }
}

// 从上往下堆化，对于完全二叉树而言，号子结点起始位置： "arr.length / 2 + 1"
public void heavify(int[] arr) {
    for (int i = arr.length / 2; i >= 1; --i) {
        // 随机数据的插入和删除，堆的长度会发生变化，需要第二个参数来控制向下堆化的最大位置
        shiftDown(i, arr.length, arr[i]);
    }
}
// 大顶堆：从上往下堆化
private static void shiftDown(int i, int size, Integer[] arr) {
    while (true) {
        int maxPos = i;
        if (size > 2 * i + 1 && arr[maxPos] < arr[2 * i + 1]) {
            maxPos = 2 * i + 1;
        }
        if (size > 2 * i + 2 && arr[maxPos] < arr[2 * i + 2]) {
            maxPos = 2 * i + 2;
        }
        if (maxPos == i) {
            break;
        }
        swap(arr, i, maxPos);
        i = maxPos;
    }
}

说明： 最核心的方法是向上堆化 shiftUp 和向下堆化 shiftDown 这两个方法，可以参考 PriorityQueue 小顶堆的实现。

2.2 排序

排序同样是将数据分为已经排序和未排序部分。其中未排序部分是一个大顶堆，依次从大顶堆中取出最大元素，插入已经排序部分。

public void sort(Integer[] arr) {
    heavify(arr);
    // 从大顶堆中取出最大元素，依次插入已经排序部分
    doSort(arr);
}

private void doSort(Integer[] arr) {
    int n = arr.length;
    for (int i = 1; i < n; i++) {
        swap(arr, 0, n - i);
        shiftDown(0, n - i, arr);
    }
}

2.3 三大指标

（1）时间复杂度

堆化时间复杂度：O(n)

                       层数   元素个数  时间复杂度  总时间复杂度
          ○             1      1          h-1     h-1    
      ○       ○         2      2          h-2     2(h-2)
    ○   ○   ○   ○       3      n/8        2       n/2^3 * 2
   ○ ○ ○ ○ ○ ○ ○ ○      4      n/4        1       n/2^2 * 1
          ...           h      n/2        0       0

S = n/2 + 2n/4 + 3n/16 + 4n/32 + 2(h-2) + (h-1) = O(n)

排序时间复杂度：O(nlogn)

如果数据原本就是有序的，堆排序在堆化过程会打乱原先的顺序，再进行排序，因此，即便是完全有序数组的时间复杂度是 O(nlogn)。但对完全逆序的数组，其时间复杂度也是 O(nlogn)。总的来说，堆排序的时间复杂度非常稳定。

（2）空间复杂度

堆排序是原地排序。

（3）稳定性

在堆化的过程中，会出现非相邻元素交换，因此堆排序是非稳定排序。

2.4 堆排序 vs 快速排序

在实际开发中，为什么快速排序要比堆排序性能好？

堆排序对 CPU 不友好。快速排序来说局部顺序访问，而堆排序则是逐层访问。比如，堆排序会依次访问数组下标是 1，2，4，8 的元素，而不是像快速排序那样，局部顺序访问。
堆排序算法的数据交换次数要多于快速排序。比如，有序数组建堆后，数据反而变得更无序。

3. 优先级队列

如 Java 中的优先级队列 PriorityQueue 和 PriorityBlockingQueue 就是使用小顶堆实现的。

合并有序小文件
高性能定时器
Top N
利用堆求中位数

每天用心记录一点点。内容也许不重要，但习惯很重要！

posted on 2018-12-13 19:32 binarylei 阅读(978) 评论(0) 编辑收藏举报

刷新页面返回顶部

binarylei