动态规划之——最长公共子序列

先看下最长公共子序列（Longest Common Subsequence）的问题描述。

给定两个字符串，求两者的最长公共子序列的长度。

子序列是指从字符串中按特定顺序（从左向右或从右向左，可以有间隔）选取的一些字符组成的序列。例如“ABCDEF”中ABC、ACD、AE、AF都是子序列。而公共子序列，就是两个字符串中相同的子序列。

例如字符串“ABC”和“BCD”构成的子序列如图-1：

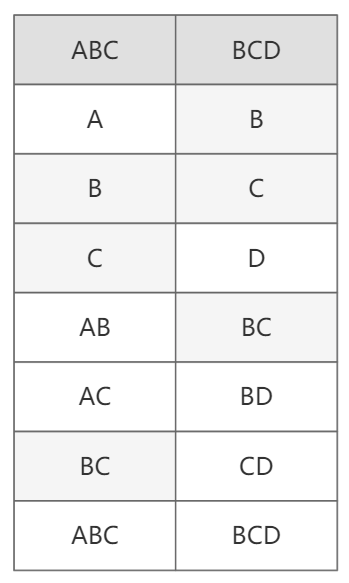
                         图-1
可以看到公共子序列有B、C、BC，因此最长的就是BC。

 

我们先分析下这个问题，能否从动态规划角度解决。如图-2，求两个字符串s1=“ABCE” 和 s2=“ACD”的最长公共子序列：

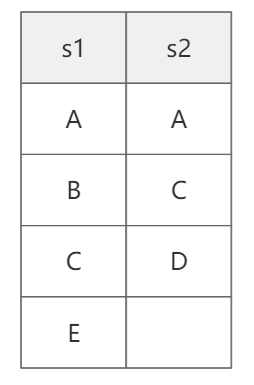
                 图-2

明显能看出来答案是“AC”，对应长度为2。我们说的“看”，其实是经过不同组合比较后得到的。

首先这两个字符串都是“A”开头，所以公共子序列中必然包括“A”，即最长公共子序列的长度至少是1，无论后续字符如何比较，都不会影响这个A。

接下来，继续对比剩余部分的BCE、CD，这时B不等于C，一种组合是继续用BCE中的字符B和CD中的D比较。

还有一种组合是用CD中的C继续和BCE中的下一个字符C比较。这里产生出两种组合。后续对比中参考同样方法：字符相同记录下来再跳过该字符，不同则继续组合……过程如图-3：

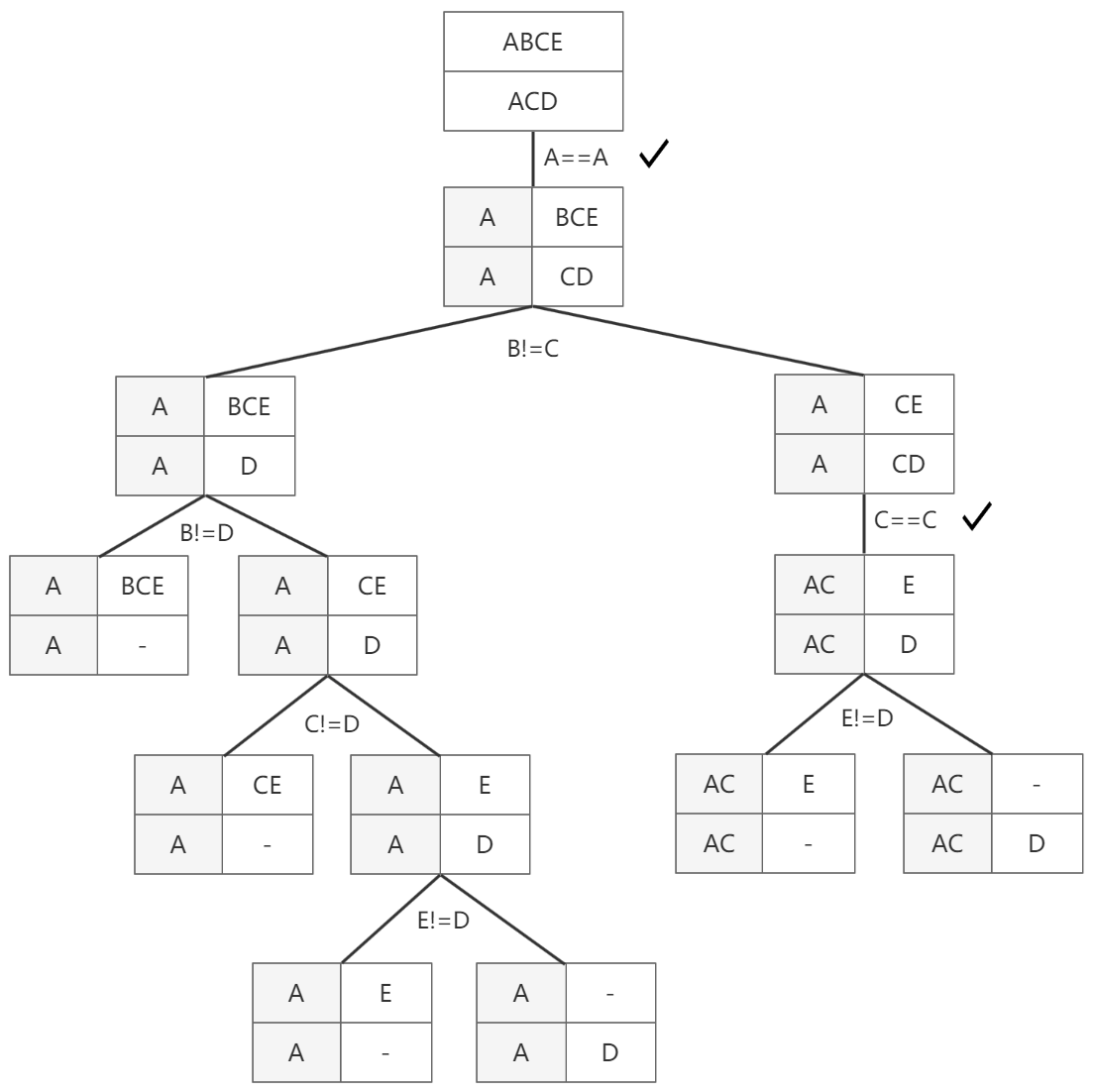
                                                                                图-3

在比较过程中，发现相等的我们就放置到表格左列。最终可以看到，在第一次出现B!=C左侧最底层分支的公共子序列仍然为“A”，而右侧最底层分支为“AC”，因此最长公共子序列为“AC”。我们用如下代码模拟此过程。

public class LongestCommonSubsequence {
    public static void main(String[] args) {
        String[] a = {"A", "B", "C", "E",};
        String[] b = {"A", "C", "D"};
        //从第一个字符开始比较
        System.out.println(compare(a, b, 0, 0));
    }

    public static int compare(String[] a, String[] b, int m, int n) {
        if (m == a.length || n == b.length) {
            return 0;
        }
        System.out.printf("%d=%s %d=%s\n", m, a[m], n, b[n]);
        //相等则两个字符串都跳转到下一个字符
        if (a[m].equals(b[n])) {
            //公共子序列长度+1
            return 1 + compare(a, b, m + 1, n + 1);
        } else {
            //字符串a的当前字符位置不变，b从下一个字符开始比较
            int x = compare(a, b, m, n + 1);
            //字符串b的当前字符位置不变，a从下一个字符开始比较
            int y = compare(a, b, m + 1, n);
            //取两者的最大值
            return Math.max(x, y);
        }
    }
}

 输出如下

0=A 0=A
1=B 1=C
1=B 2=D
2=C 2=D
3=E 2=D
2=C 1=C
3=E 2=D
2

可以看到代码通过递归不断向右侧移动字符，直到对比完毕。同时输出中存在重复比较（3=E 2=D）。因此可以尝试用动态规划的思路来优化，依照如下规则从最左侧字符开始向右移动计算：

规则1 字符相等时，取之前的匹配结果的子序列长度加1

规则2 字符不等时，取拆分出来的两种组合中的最大值。

代码如下，增加compareDp方法

public static int compareDp(String[] a, String[] b) {
        //由于第一个字符需要和一个空字符比较，相当于两个字符串长度都加1，所以多申请一个长度
        int[][] dp = new int[a.length + 1][b.length + 1];
        //dp数据初始化：由于每个字符串增加一个逻辑意义上的空字符，而空字符和非空字符不相等，所以都设置为0
        for (int i = 0; i < a.length + 1; i++) {
            dp[i][0] = 0;
        }
        for (int j = 0; j < b.length + 1; j++) {
            dp[0][j] = 0;
        }

        //从下标为1的位置开始，方便和前一个字符比较
        for (int i = 1; i <= a.length; i++) {
            for (int j = 1; j <= b.length; j++) {
                System.out.printf("%d-%d\n", i, j);
                //相等则该位置对应的公共子序列长度为之前的公共子序列长度+1
                if (a[i - 1].equals(b[j - 1])) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                    System.out.printf("\t%s=%s %d+1=%d\n", a[i - 1], b[j - 1], dp[i - 1][j - 1], dp[i][j]);
                } else {
                    //从拆分的两种组合中获取一个最大的数值
                    dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
                    System.out.printf("\t%s!=%s %d %d\n", a[i - 1], b[j - 1], dp[i][j - 1], dp[i - 1][j]);
                }
            }
        }

        for (int i = 0; i < a.length + 1; i++) {
            System.out.printf("%d: ", i);
            for (int v : dp[i]) {
                System.out.printf("%d ", v);
            }
            System.out.println();
        }
        return dp[a.length][b.length];
    }

调用compareDp(a, b)，输出如下

1-1
	A=A 0+1=1
1-2
	A!=C 1 0
1-3
	A!=D 1 0
2-1
	B!=A 0 1
2-2
	B!=C 1 1
2-3
	B!=D 1 1
3-1
	C!=A 0 1
3-2
	C=C 1+1=2
3-3
	C!=D 2 1
4-1
	E!=A 0 1
4-2
	E!=C 1 2
4-3
	E!=D 2 2
0: 0 0 0 0 
1: 0 1 1 1 
2: 0 1 1 1 
3: 0 1 2 2 
4: 0 1 2 2 
2

计算依赖关系如图-4。第一行和第一列需要初始化为0。单个箭头表示字符相同时取之前部分的公共子序列长度加1，如dp[1][1]、dp[3][2]。两个箭头表示字符不同时取两种组合的最大值，如dp[1][2]、dp[1][3]

仅标识出了部分计算依赖，其他可参考此方法。

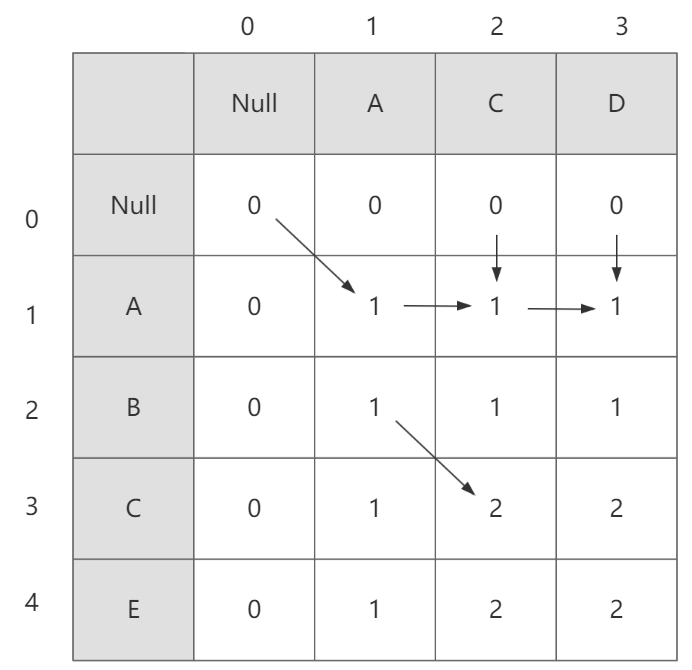
                                                   图-4

这里再说明下字符不等时的处理逻辑 dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j])

如果参考之前的递归方法，直觉上是 Math.max(dp[i][j + 1], dp[i + 1][j])，但此时并未处理到后续的数据，读取结果必然是0。

正确的依赖应该是已计算过的数据。

例如，处理dp[3][3]时，表面看对比的字符为C和D，其实对应的完整字符串是“ABC”和“ACD”，对比的是这两个字符串中最后的字符C和D，这时要取C!=D产生的两种组合，即

组合1：ABC和AC，即dp[3][2]

组合2：AB和ACD，即dp[2][3]

而这两种组合的结果是之前已经计算过的，因此对应的dp数组下标值要减1。

另外可以考虑下，如果递归时从右侧向左处理结果会如何？

 

参考资料
Longest Common Subsequence | DP-4

动态规划3-最长公共子序列问题