动态规划之——矩阵连乘问题
先看问题描述:
给定7个数字30、35、15、5、10、20、25,只能相邻的两个数字组成矩阵,即:30*35、35*15、15*5、5*10、10*20、20*25共计6个矩阵,且只能相邻的两个矩阵相乘。求矩阵最小的相乘次数。
我们先解释下什么是矩阵相乘(Matrix Multiplication),即用矩阵1的每一行值按顺序分别乘以矩阵2的每一列(矩阵1的列数必须等于矩阵2的行数),再把各个乘积相加。
例如一个3行2列的矩阵乘以一个2行4列的矩阵,得到一个3*4的矩阵。如图-1
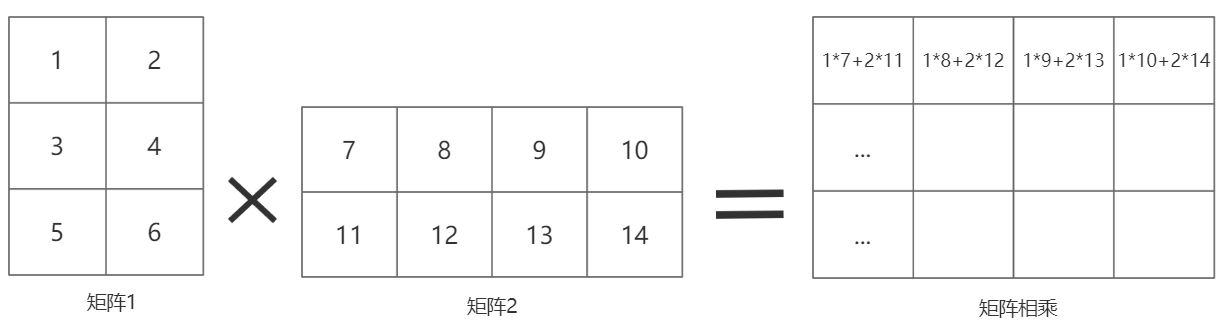
图-1
可以看到相乘的次数和行数、列数是有关系的:
看矩阵相乘结果的第一行里的数量,等于另外一个矩阵的列数(4列)。矩阵一共3行,则3*4=12次。
再看某个值的相乘次数:矩阵1的列数等于矩阵2的行数,由于需要分别相乘,则矩阵1有几列(或者矩阵2有几行)对应就要乘以几次。
因此12次的相乘中,每次相乘又包含了2次相乘,所以最终相乘的次数为3*4*2=24次。
同理5*10、10*3两个矩阵相乘的次数为5*3*10=150次。
因此我们得到两个公式:
【公式1】 a行b列的矩阵(a*b)和b行c列的矩阵(b*c)相乘,结果为一个a行c列(a*c)的矩阵
【公式2】 a*b和b*c的两个矩阵相乘,对应的乘法次数为a*b*c
有了这些背景知识,我们再回到原问题。6个矩阵30*35、35*15、15*5、5*10、10*20、20*25,分别记作矩阵a、b、c、d、e、f。我们以其中的矩阵a、b、c为例,则会有两种组合
组合1 a(bc)=(30*35)(35*5)+35*15*5=30*35*5+2625=7875
组合2 (ab)c=30*35*15+(30*15)(15*5)=15750+30*15*5=18000
可以看到不同顺序的矩阵相乘得到的相乘次数是不一样的。所以,求解此问题直观的方法还是穷举,即计算这些组合的乘积次数,取最小值。但是随着矩阵数量增多,对应的组合也会指数级别增多。
有没有其他更好的办法呢?
我们再分析一下问题:显然是一个求解最优值的问题,即求最少的乘法次数。为了方便说明我们把矩阵转换为下标形式,如图-2,用每个下标对应一个矩阵
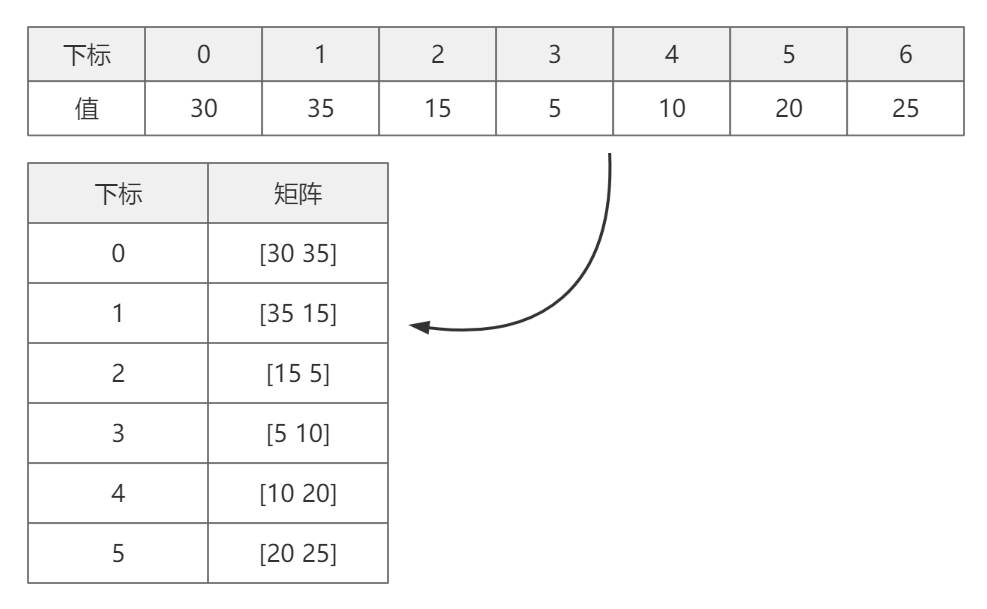
图-2
演示数据参考于 数据结构与算法分析新视角,电子工业出版社
我们先尝试从较小的范围组合求解,看下是否存在一个最优解。如求解(0-3)矩阵,可拆解成如下步骤
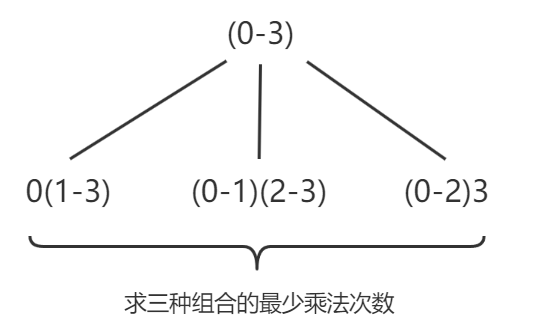
图-3
(0-3)表示矩阵下标为0、1、2、3的四个矩阵
如果能分别这求出这三个组合的乘法次数,再取最小值,即为(0-3)矩阵的最优值。但当求其中一个组合时,又可以再细分下去,如0(0-3)组合中的(1-3)又可用分为两种
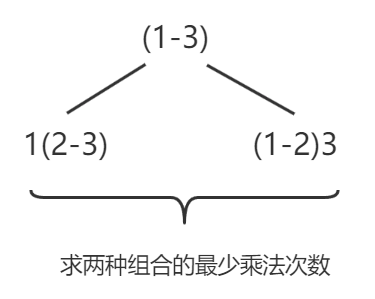
图-4
而如果再细分1(2-3),则又分出(2-3)的结果,可见整个依赖关系是不断向下传导的:求(0-3)需先求出(1-3),(1-3)又需要求出(2-3)……
因此为了计算整体结果,则需要从最小粒度向上逐步计算,是一个由底部逐渐向上递推并最终收敛的过程。
对应过程如图-5,从最左侧最小间隔(即最小粒度的两两矩阵组合,或者称为最小区间)开始,向右侧间隔依次增大,直到最大的区间(0-5),即最终最优值对应的区间。
结合图-3和图-4能看到间隔3中的(0-3)分别直接依赖了左侧间隔2中的(1-3),以及间接依赖的间隔1中的(1-2)、(2-3),并且每个间隔只依赖左侧已确定的结果,因此每个间隔计算的结果只作用于当前间隔。
同时如果我们分解其他组合也会出现重复的组合,例如间隔3中的(1-4),分解过程中必然会出现(1-3)4的组合,而(1-3)由之前的分解可以看到是依赖了间隔1中的(1-2)和(2-3),因此我们可以把这些重复的组合保存下来,用于后续计算。这点类似于背包问题和斐波那契数列用到的结果表。
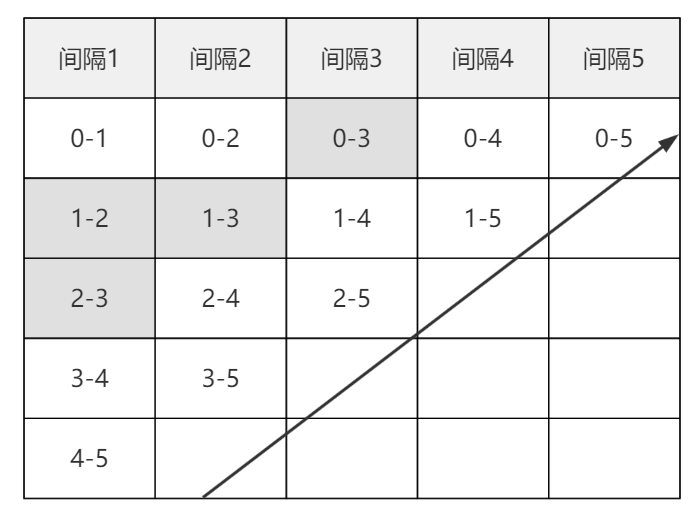
图-5
我们根据这个思路编写如下代码,演示数据同图-2
1 public class MatrixMulti { 2 public static void main(String[] args) { 3 int[] matrix = {30, 35, 15, 5, 10, 20, 25}; 4 System.out.println(Arrays.toString(matrix)); 5 calc(matrix); 6 } 7 8 private static void calc(int[] matrix) { 9 int num = matrix.length; 10 //最小间隔 11 int minDistance = 1; 12 //最大间隔 13 int maxDistance = num - 2; 14 //各个矩阵组合的最小乘积数(矩阵相乘中出现的乘法次数) 15 int[][] dp = new int[num - 1][num - 1]; 16 for (int i = 0; i < num - 1; i++) { 17 //数据的初始化:矩阵自身的乘积数是0 18 dp[i][i] = 0; 19 System.out.println(i + ":" + matrix[i] + " " + matrix[i + 1]); 20 } 21 //从最小间隔开始,依次增大 22 for (int distance = minDistance; distance <= maxDistance; distance++) { 23 System.out.println("distance " + distance); 24 //从第一个矩阵开始,一直到符合间隔数的最后一个矩阵 25 for (int start = 0; start < num - distance - 1; start++) { 26 int end = start + distance; 27 System.out.println("\trange " + start + "-" + end + " "); 28 //矩阵默认的最小乘积为最大值 29 dp[start][end] = Integer.MAX_VALUE; 30 //在开始矩阵和结束矩阵中间不断加入新的间隔矩阵,求出一个最小乘积数 31 for (int mid = start; mid < end; mid++) { 32 //引入间隔矩阵后,对应的乘积数的计算公式:开始矩阵到间隔矩阵的乘积数+间隔矩阵到结束矩阵的乘积数+开始矩阵的行数*间隔矩阵的列数*结束矩阵的列数 33 int sum = dp[start][mid] + dp[mid + 1][end] + matrix[start] * matrix[mid + 1] * matrix[end + 1]; 34 System.out.printf("\t\tstart=%d mid=%d, mid+1=%d end=%d, sum=%d+%d+(%d*%d*%d=%d)=%d\n", 35 start, mid, mid + 1, end, dp[start][mid], dp[mid + 1][end], 36 matrix[start], matrix[mid + 1], matrix[end + 1], 37 matrix[start] * matrix[mid + 1] * matrix[end + 1], sum); 38 if (sum < dp[start][end]) { 39 dp[start][end] = sum; 40 } 41 } 42 System.out.println("\tmin " + dp[start][end]); 43 } 44 } 45 for (int i = 0; i < num - 1; i++) { 46 System.out.println(i + ":" + Arrays.toString(dp[i])); 47 } 48 } 49 }
输出
[30, 35, 15, 5, 10, 20, 25] 0:30 35 1:35 15 2:15 5 3:5 10 4:10 20 5:20 25 distance 1 range 0-1 start=0 mid=0, mid+1=1 end=1, sum=0+0+(30*35*15=15750)=15750 min 15750 range 1-2 start=1 mid=1, mid+1=2 end=2, sum=0+0+(35*15*5=2625)=2625 min 2625 range 2-3 start=2 mid=2, mid+1=3 end=3, sum=0+0+(15*5*10=750)=750 min 750 range 3-4 start=3 mid=3, mid+1=4 end=4, sum=0+0+(5*10*20=1000)=1000 min 1000 range 4-5 start=4 mid=4, mid+1=5 end=5, sum=0+0+(10*20*25=5000)=5000 min 5000 distance 2 range 0-2 start=0 mid=0, mid+1=1 end=2, sum=0+2625+(30*35*5=5250)=7875 start=0 mid=1, mid+1=2 end=2, sum=15750+0+(30*15*5=2250)=18000 min 7875 range 1-3 start=1 mid=1, mid+1=2 end=3, sum=0+750+(35*15*10=5250)=6000 start=1 mid=2, mid+1=3 end=3, sum=2625+0+(35*5*10=1750)=4375 min 4375 range 2-4 start=2 mid=2, mid+1=3 end=4, sum=0+1000+(15*5*20=1500)=2500 start=2 mid=3, mid+1=4 end=4, sum=750+0+(15*10*20=3000)=3750 min 2500 range 3-5 start=3 mid=3, mid+1=4 end=5, sum=0+5000+(5*10*25=1250)=6250 start=3 mid=4, mid+1=5 end=5, sum=1000+0+(5*20*25=2500)=3500 min 3500 distance 3 range 0-3 start=0 mid=0, mid+1=1 end=3, sum=0+4375+(30*35*10=10500)=14875 start=0 mid=1, mid+1=2 end=3, sum=15750+750+(30*15*10=4500)=21000 start=0 mid=2, mid+1=3 end=3, sum=7875+0+(30*5*10=1500)=9375 min 9375 range 1-4 start=1 mid=1, mid+1=2 end=4, sum=0+2500+(35*15*20=10500)=13000 start=1 mid=2, mid+1=3 end=4, sum=2625+1000+(35*5*20=3500)=7125 start=1 mid=3, mid+1=4 end=4, sum=4375+0+(35*10*20=7000)=11375 min 7125 range 2-5 start=2 mid=2, mid+1=3 end=5, sum=0+3500+(15*5*25=1875)=5375 start=2 mid=3, mid+1=4 end=5, sum=750+5000+(15*10*25=3750)=9500 start=2 mid=4, mid+1=5 end=5, sum=2500+0+(15*20*25=7500)=10000 min 5375 distance 4 range 0-4 start=0 mid=0, mid+1=1 end=4, sum=0+7125+(30*35*20=21000)=28125 start=0 mid=1, mid+1=2 end=4, sum=15750+2500+(30*15*20=9000)=27250 start=0 mid=2, mid+1=3 end=4, sum=7875+1000+(30*5*20=3000)=11875 start=0 mid=3, mid+1=4 end=4, sum=9375+0+(30*10*20=6000)=15375 min 11875 range 1-5 start=1 mid=1, mid+1=2 end=5, sum=0+5375+(35*15*25=13125)=18500 start=1 mid=2, mid+1=3 end=5, sum=2625+3500+(35*5*25=4375)=10500 start=1 mid=3, mid+1=4 end=5, sum=4375+5000+(35*10*25=8750)=18125 start=1 mid=4, mid+1=5 end=5, sum=7125+0+(35*20*25=17500)=24625 min 10500 distance 5 range 0-5 start=0 mid=0, mid+1=1 end=5, sum=0+10500+(30*35*25=26250)=36750 start=0 mid=1, mid+1=2 end=5, sum=15750+5375+(30*15*25=11250)=32375 start=0 mid=2, mid+1=3 end=5, sum=7875+3500+(30*5*25=3750)=15125 start=0 mid=3, mid+1=4 end=5, sum=9375+5000+(30*10*25=7500)=21875 start=0 mid=4, mid+1=5 end=5, sum=11875+0+(30*20*25=15000)=26875 min 15125 0:[0, 15750, 7875, 9375, 11875, 15125] 1:[0, 0, 2625, 4375, 7125, 10500] 2:[0, 0, 0, 750, 2500, 5375] 3:[0, 0, 0, 0, 1000, 3500] 4:[0, 0, 0, 0, 0, 5000] 5:[0, 0, 0, 0, 0, 0]
通过求解过程,我们发现此问题和背包问题的整体思路是一致的,两者都分为了不同的阶段(区间),每个阶段有自己的最优值,且最优值只影响当前阶段,并且后续阶段依赖到了先前阶段的最优值。
引入间隔矩阵mid是算法的核心所在,这点类似于求最短路径的Floyd算法中对中间顶点的引入,都可以看作是一种枚举(试探)。
另外,可以想一下如何推导出最优值对应的矩阵具体组合。
输出中的粗体部分也许能给你些提示。
参考资料
数据结构与算法分析新视角,电子工业出版社,2016-03,ISBN: 9787121280849


 浙公网安备 33010602011771号
浙公网安备 33010602011771号