动态规划之——01背包问题

动态规划（Dynamic Programming，DP）是运筹学的一个分支，是求解决策过程最优化的过程。 ——引用于百度百科

我们先从一个例子看下动态规划的思想。

有一个最大负重为8千克的背包。现有四个物品，对应的名称、重量、价值如图-1

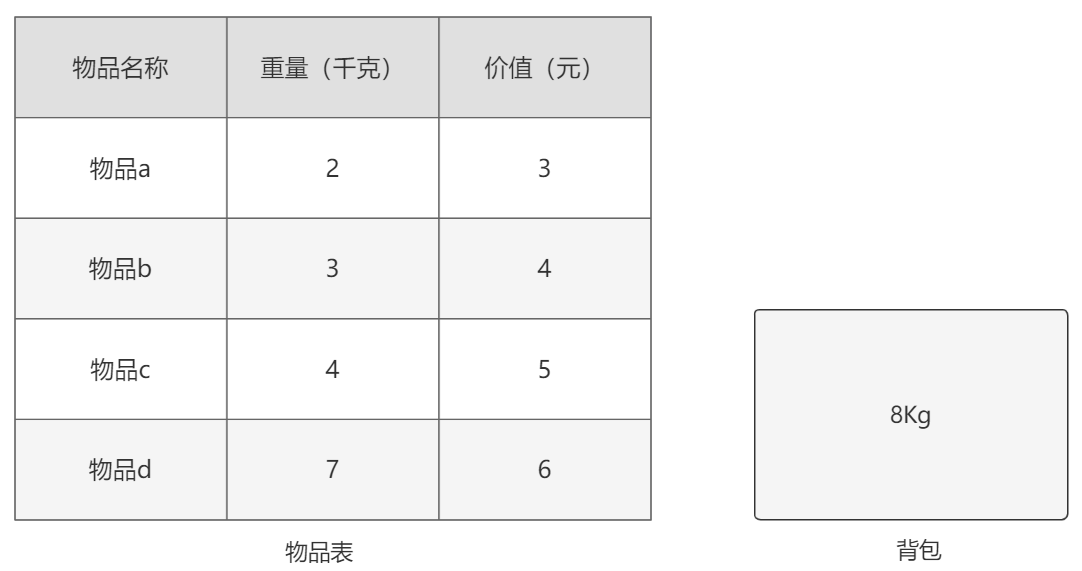
                                                                                  图-1

 求在背包负重范围内，使装进背包物品的价值之和最大。

由于每件物品都要决定是否装入，对应结果为装入1或不装入0，因此称为01背包问题（0-1 Knapsack Problem）

 

如何装呢？

直觉的办法可能是对价值从大到小排序，先装价值最大的物品。即先装入物品d，价值为6，这时可用负重还剩8-7=1千克，发现其他物品已经无发再装入了，此时最大价值为6元。

或者对重量从小到大排序，先装重量轻的物品。即先装入物品a，此时还剩8-2=6千克，再装入物品b后，剩余3千克可用负重，此时已无法再装入，最大价值为3+4=7元。

这两种方法遵循的是“贪心算法”（Greedy Algorithm），即每次都取当前情况下的最优值，以期望最终达到整体的最优。例如之前介绍的哈夫曼编码、求最短路径的Dijkstra算法、介绍图的基本概念时计算最小生成树的Prim和Kruskal算法都是典型的贪心算法。但解决此问题却是无效的，可用看到存在物品b、c组合，对应价值为9元，大于之前的两种组合。

 

还有其他办法吗？

也许还能想到枚举：在不超过负重的情况下尝试各种组合。例如两个物品组合的ab、ac、ad、bc、bd、cd以及三个物品组合的abc、acd、bcd，再取承重范围内各组合的最大值。这的确是一种办法，如果物品数量不多，确实可以解决问题。但似乎感觉还有更好的办法。

 

我们换种思路，从最终结果出发。

 

假设我们已经获得最大价值，并且假设四件物品都已经装入（当然在此例中是不可能的）。这时能明确的只是已无物品可装了。所以我们退回到三件物品的阶段，假设此时同样达到了最大价值X（当然也有可能实际背包中小于三件物品，这里我们认为就是三件，表示所处的一个阶段）。

我们这时模拟第四件物品d的装入情景：当装入第四件物品d时，它的重量为7千克，我们假设它可以装入，则会占用7千克的负重，那么此时背包还剩余1千克的负重。

再看这剩余的1千克负重在当前物品件数（即之前假设的三件，实际背包中不一定为三件）时可装的最大价值是多少？假设为Y。于是我们把Y和要装入物品d的价值7相加和，得到一个新的累计价值Z（Y+7），再和当前阶段的价值X比较。如果Z大于X，说明应该把此时背包中的某些（某个）物品取出来，而装入物品d。

而如果Z小于X，那就保持原有物品不动（说明装入后价值反而变小了）。

 

同理我们可继续模拟物品c、d的装入，不同的只是阶段对应的物品数量不同，物品c对应两件物品时的状态，物品b对应一件物品时的状态……

直到装入第一件物品a时：此时背包中是空的，物品a重量为2千克，则装入后背包剩余8-2=6千克。由于此阶段背包中物品为空，所以剩余的6千克对应的可装的最大价值必然是0。0+3大于0，则此时背包对应最大价值3。

计算出此时的背包最大值是否可以进行第二件物品了呢？

不行。

如果后续放置其他物品后背包剩余重量是0、1、2、3、4、5、6、7千克的怎么办呢？

所以需要把各种负重下对应的价值都计算出来：

剩余0千克时必然价值也为0；

剩余1千克负重时，物品a不能装入，所以价值也为0；

剩余2千克时可以装入，2-2=0，同理0千克剩余必然价值也为0，0+3大于0，所以价值还是3元；

用同样的方法计算余下的3——8负重，都是3元。

这样再加入其他物品时就可以直接读取这些初始值做判断了（准确说应该是当计算第一件物品装入时，已经有物品为0这个阶段的初始值了，只不过物品为空，对应的最大价值全部为0）。

 

我们再总结一下。

如果每次新装入一个物品之前，都知道已累计装入的物品的最高价值，并且知道背包可用负重减去此物品重量后的剩余重量对应的最大价值，那么我们就能判断这个物品该不该装入。能装入则更新为新的最大价值，不能装入则仍保留之前的最大价值。

因此我们需要维护一个阶段（某物品数量下）的每种重量（0-8千克）对应的最大价值的信息表。因此我们才会去设计一个二维的数组“dp[i][j]=v”来存储当前物品数量时的最大价值：其中i表示i个物品，j是j个负重（千克），即第i个物品的j个重量时对应的最大价值为v。

例如当dp[2][3]=4，表示2件物品时，3千克负重对应的背包物品的最大价值为4元。

注意！一定要理解dp[2][3]的重量3千克的含义。它表示的是两种视角下的3千克：

视角一，从已加入到背包中的物品来看，3千克是已用负重对应的装入物品的最大价值，是为了方便后续查找此重量对应的价值而产生的数据。

视角二，从将要装入的物品的视角来看，3千克是可用负重，转换为了上一个阶段存储了价值为v的物品后还剩余的3千克可用负重。所以如果此阶段要装入一个2千克的物品，则需要用3千克减去此物品重量，即3-2=1（而不是8-2），再取这剩余的1千克重量（这时视角又转换为已加入背包的物品，要取上一个阶段的数据）对应的最大价值来进行加和比较的。

这里涉及到一个视角的转换，会比较绕，但也是算法的核心所在，希望大家仔细斟酌。

还有是刚接触此类问题，判断一个物品该不该装入时，直觉认为如果一个物品能装入，肯定是要装入啊，因为只有装入后价值才会更高。其实并不是和当前价值相加后再和当前价值比较，而是该物品装入后和剩余负重还能装入的重量对应的价值之和，拿这个加和数再与当前价值比较。

 

实现代码和输出如下，演示的背包数据同图-1。

public class Knapsack {
    //背包负重
    private static int knapsackWeight;
    //物品个数
    private static int itemNum;
    //物品数组
    private static Item[] items;
    //物品个数+重量对应的最大价值
    private static int[][] dp;

    public static void main(String[] args) {
        initDemo();

        //第一件物品对应下标从1开始
        for (int i = 1; i < itemNum; i++) {
            //未存入此物品之前的物品的累计数量，由于物品数量是递增的，之前的即当前的物品下标减1
            //这里一定要注意：不是物品加入后物品数量才递增，而是比较完毕即加1。
            int prevItem = i - 1;
            //剩余重量从0-8都需要处理，这样才能计算出每种剩余重量对应的最大价值。
            for (int j = 0; j <= knapsackWeight; j++) {
                //当前的剩余重量能装下时再判断，否则保持不动
                if (j >= items[i].weight) {
                    //注意这里是用“当前剩余重量”减去当前物品的重量，而不是用背包的重量
                    int leftWeight = j - items[i].weight;
                    int newValue = dp[prevItem][leftWeight] + items[i].value;
                    //剩余重量对应的最大价值加上新物品的价值 大于之前背包中累计物品的最大价值，说明要把当前这个物品放入。否则就保持不动。
                    if (newValue > dp[prevItem][j]) {
                        dp[i][j] = newValue;
                    } else {
                        dp[i][j] = dp[prevItem][j];
                    }
                } else {
                    dp[i][j] = dp[prevItem][j];
                }
            }
        }
        print();
    }

    private static void initDemo() {
        //设置背包最大负重
        knapsackWeight = 8;
        //加入了空物品，实际有效物品为4个。
        itemNum = 5;
        items = new Item[itemNum];
        //第一个元素设置为空
        items[0] = new Item("-", 0, 0);
        items[1] = new Item("a", 2, 3);
        items[2] = new Item("b", 3, 4);
        items[3] = new Item("c", 4, 5);
        items[4] = new Item("d", 7, 6);
        //需要考虑剩余负重为0的最大价值，所以增加一个重量为0的列
        //初始化数据时第0个物品和剩余为0重量的背包对的最大价值必须初始化为0（由于Java int数组值默认为0，所以这里没有单独初始化0）
        dp = new int[itemNum][knapsackWeight + 1];
    }

    private static void print() {
        System.out.print("W  ");
        for (int j = 0; j < dp[0].length; j++) {
            System.out.printf("%d  ", j);
        }
        System.out.println();
        for (int i = 0; i < itemNum; i++) {
            System.out.printf("%s  ", items[i].name);
            for (int j = 0; j < dp[i].length; j++) {
                System.out.printf("%d  ", dp[i][j]);
            }
            System.out.println();
        }
    }

    private static class Item {
        private final String name;
        private final int weight;
        private final int value;

        public Item(String name, int weight, int value) {
            this.name = name;
            this.weight = weight;
            this.value = value;
        }

        @Override
        public String toString() {
            return "Item{" + "name='" + name + '\'' + ", weight=" + weight + ", value=" + value + '}';
        }
    }
}

 

W  0  1  2  3  4  5  6  7  8  
-  0  0  0  0  0  0  0  0  0  
a  0  0  3  3  3  3  3  3  3  
b  0  0  3  4  4  7  7  7  7  
c  0  0  3  4  5  7  8  9  9  
d  0  0  3  4  5  7  8  9  9

流程图

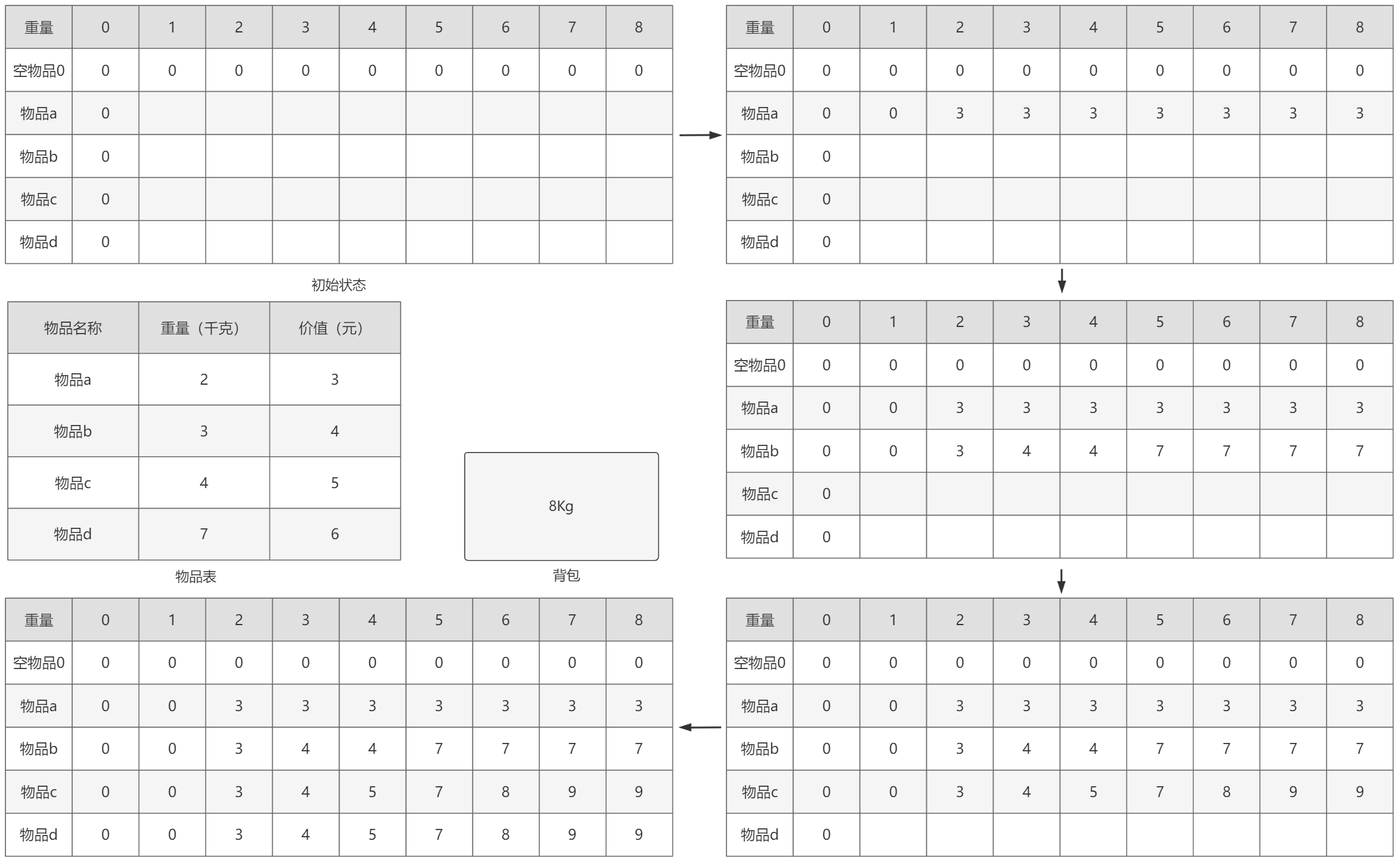
                                                                                                                                                                           图-2

接下来我们再看个简单的例子，斐波那契数列，为何它是如此简单。

斐波那契数列是指的是这样一个数列：1、1、2、3、5、8……从第三个数开始，其值等于前两个数之和。例如

n=3，1+1=2

n=4，2+1=3

n=5，3+2=5

现在求解n=7时数列的值。根据数列的特性，继续求和：

n 数值

6 5+3=8

7 8+5=13

对应代码较简单，使用递归来实现。

public class Fibonacci {
    public static void main(String[] args) {
        //1、1、2、3、5、8、13……
        int n = 7;
        System.out.printf("n=%d %d\n", n, calc(n));
    }

    private static int calc(int n) {
        if (n <= 1) {
            return n;
        }
        return calc(n - 1) + calc(n - 2);
    }
}

求解过程中我们能发现：

1 每一步（n>2时）使用了之前的计算结果

2 每一步的计算结果只会影响该步的值，并不会修改之前的结果。

3 整个过程是分阶段，逐步计算出来的。 

由于每一步只是读取前一步的计算结果，因此我们可以用一个表（数组）来存在之前计算结果，以减少重复计算（典型的空间换时间）。

public class FibonacciV2 {
    public static void main(String[] args) {
        int n = 7;
        int[] arr = new int[n + 1];
        System.out.printf("n=%d: calc %d, calcArray %d, calcArrayDp %d", n, calc(n), calcArray(n, arr), calcDp(n, arr));
    }

    private static int calc(int n) {
        if (n <= 1) {
            return n;
        }
        return calc(n - 1) + calc(n - 2);
    }

    private static int calcArray(int n, int[] arr) {
        if (arr[n] > 0) {
            return arr[n];
        }
        if (n <= 1) {
            arr[n] = n;
            return n;
        }
        arr[n] = calcArray(n - 1, arr) + calcArray(n - 2, arr);
        return arr[n];
    }

    private static int calcDp(int n, int[] arr) {
        arr[1] = 1;
        arr[2] = 1;
        for (int i = 3; i <= n; i++) {
            arr[i] = arr[i - 1] + arr[i - 2];
        }
        return arr[n];
    }
}

 calcArray方法使用一个数组来存储之前的计算结果，仍然通过递归方式调用。calcDp方法则是直接依赖之前的调用结果，通过循环来加和，避免了递归调用。

再看01背包问题，同样用一个dp数组来存储前一步的计算结果。从这个角度看，动态规划可看作是对算法的一种优化，把子问题的结果存储在一个表内，供后续步骤使用。

而难点是如何正确划分出子问题并确定子问题的结果。斐波那契数列问题之所以简单，是因为开始就明确了方法：“其值等于前两个数之和”，而前两个数的结果calc(n-1)和calc(n-2)是不会再改变了。但从求解过程中能发现，本质上两者的思路是一样的，都属于动态规划。

这里我们引用教材中对动态规划的一种更详细的定义：“动态规划方法采用最优原则来建立用于最优解的递归式……动态规划中的每一步决策还要考察每个最优决策序列中是否包含一个最优子序列……常用于求解一个问题在某种意义下的最优解……”  ——引用于数据结构与算法（C++语言版），电子工业出版社，2009年出版

我们之前介绍的求最短路径的Floyd算法使用的正是此思想。后续我们会再看一些其他例子，加深对动态规划的理解。

 

参考资料

Dynamic Programming

动态规划

动态规划DP0-1背包

数据结构与算法（C++语言版），电子工业出版社，2009-05，ISBN: 9787121083013