关键路径

上一篇文章我们介绍了AOV网，并通过拓扑排序列出了活动的依赖顺序图。拓扑排序中我们关注的是依赖关系，没有考虑每个活动的完成时间，而在项目管理中要知道各个活动的时长才能计算出项目整体的完成时间。

我们需要加入对活动完成时间的考量，而图中的权重就可以用来表示完成时间。因此对应的具体数据结构是一种带权重的有向无环图，对应的活动表示图称为AOE网（Activity On Edge），用边（Edge）来表示活动，顶点表示事件。事件可以看作是各个活动完成后达到的一种状态，也可以认为是一个里程碑事件，依赖于各个活动的完成情况。或者可以把顶点理解成任务节点，而各个边是不同的“子任务”。

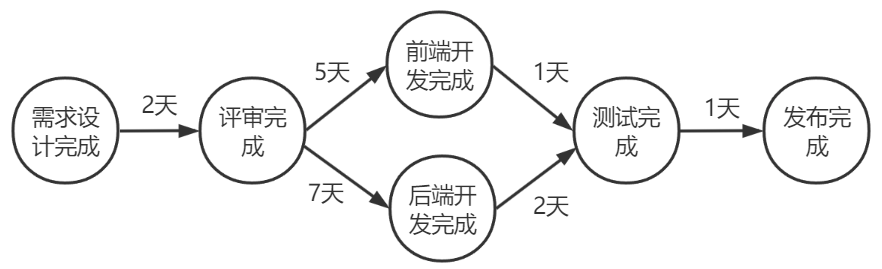
                                                            图-1

转换为AOE网的形式，如图-2

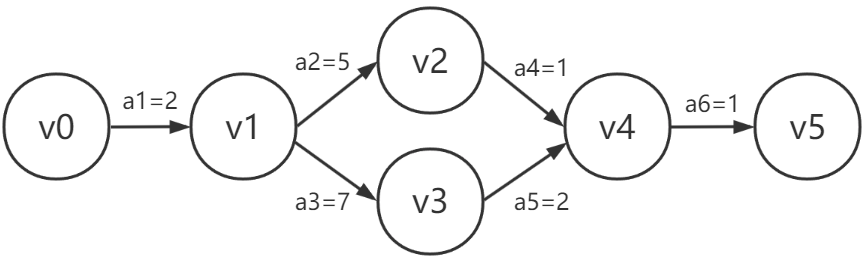
                                                           图-2

图-2的各个顶点表示事件，边表示活动，箭头尾部（出边）表示活动开始，箭头头部（入边）表示活动完成。边上的数值表示此活动的完成时间。例如v0为一个事件，活动a1表示v0-v1间的一条路径，完成时长为2天。

AOE网中一些活动是可以同时进行的。例如活动a2和a3、a4和a5。既然是同时进行，假如各自完成时间不一致，则必然存在时间差，一个较早完成，一个较晚完成，而完成时间短意味着此活动是存在空余时间的，即使晚一段时间开始也不会影响整体时间。

而完成时间长的活动必须按时完成，晚了就会影响整体完成时间，这种活动在项目管理中需要重点关注，属于关键的活动，即关键路径（Critical Path）。

 

我们先看下存在并行活动依赖的v4，如何确定它的发生时间（我们把事件的出现定义为发生，表示的是一个状态，以区别于活动的开始和结束）。v4依赖了两条路径v0-v1-v2-v4和v0-v1-v3-v4，对应的活动花费时间总和分别是

路径1：2+5+1=8天

路径2：2+7+2=11天

虽然路径1花费8天就可以完成，但还要等待11天的路径2完成后，v4事件才能发生。所以v4的最早发生时间就是路径2的完成时间，为11天（事件的最早发生时间取决于最长路径的完成时间）。

提到了最早发生时间，那么有最晚发生时间吗？“最晚”意味着不能再晚了，再晚就影响后续活动的完成时间了，因此最晚发生时间是由后续活动来确定的，由于v4的后续只有一个活动a6，那么最晚发生时间也是11天。

 

再看v2，最早发生时间是v0-v1-v2之间活动的完成时间，为2+5=7天。最晚发生时间呢？我们看它的后续活动，虽然也只有一个a4，但还存在一条并行的活动a5也指向v4，这条路径对应的活动时间累计为2+7+2=11天。

而v0-v1-v2-v4累计总时间为2+5+1=8天，两条路径相差了3天（11-8），也就是v0-v1-v2-v4这条路径累计时长比v0-v1-v3-v4快3天，意味着v2可以晚3天发生也不会影响v4，因此v2的最晚发生时间是10（11-1）。

同理，我们计算出v3的最早发生时间是9（2+7），最晚发生时间也是9（11-2）。既然最早和最晚的发生时间一样，说明v3这个事件不能再晚发生了，再晚就影响后续活动了。

 

再看下后续有多个活动依赖的v1的最晚发生时间。

依赖——v2的最晚发生时间刚才已得出为10，而a2=5，说明在v1-v2这个路径上，v1最晚需要10-5=5时发生。

依赖——v3的最晚发生时间也已得出为9，而a3=7，说明在v1-v3路径上，v1最晚需要9-7=2时发生。

得出了两个最晚发生时间5和2，选哪个呢？

这时需要考虑完成时间较长的那个活动，因为只有开始时间越早，完成时间花费长的活动a3才能确保完成。因此v1的最晚开始时间是2。同时v1的最早开始时间也是2。

 

我们再整理下思路：

1 由于存在完成时间不同的并行活动，导致事件的最早发生时间和最晚发生时间不同。

2 最早和最晚发生时间的不同说明对应的路径中存在空余时间，而不存在空余时间的路径就是关键路径。

因此我们得出以下计算方法

事件
1 最早发生时间，取决于依赖的活动中的最长的完成时间

2 最晚发生时间，取决于后续事件的最晚发生时间和各自活动的完成时间之差的最小值。

活动
1 最早开始时间，等于依赖事件的最早发生时间

2 最晚开始时间，等于后续事件的最晚发生时间减去此活动时间。

最后再看下依赖关系，上述的所有计算是基于按依赖关系排序好的顶点来计算事件的发生时间的，而依赖关系排序就是之前提到的“拓扑排序”。因此需要对图进行拓扑排序后再计算事件的发生时间。

可以想想为何要先排序，上图中如果先计算v4的最早发生时间，再计算v2的是否可以呢？

 

根据以上思想我们编写如下代码，对应的演示数据如图-3

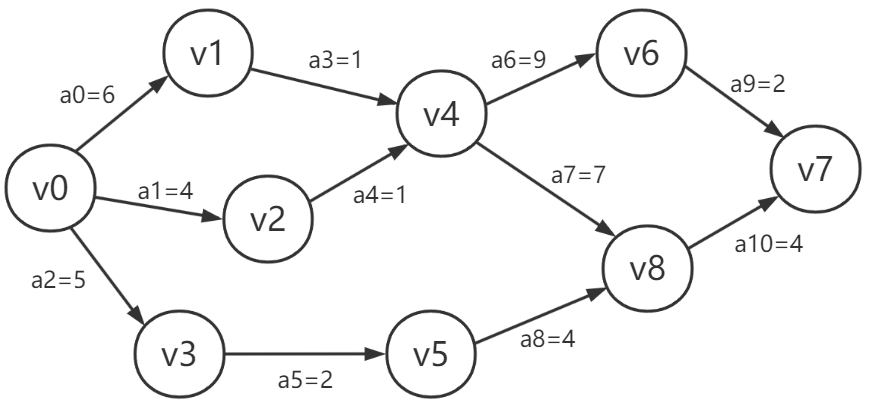
                                                                   图-3

演示数据参考于 关键路径 https://www.bilibili.com/video/BV1PW41187vc

import java.util.*;

public class CriticalPath {
    private int vertexNum;
    private List<Vertex>[] graph;
    int[] sort;

    public static void main(String[] args) {
        CriticalPath cp = new CriticalPath();
        cp.initDemo();
        cp.criticalPath();
    }

    public void criticalPath() {
        //通过Kahn算法生成拓扑序列
        kahn();

        //顶点（事件）的最早发生时间
        int[] vertexEarly = new int[vertexNum];
        calcVertexEarly(vertexEarly);

        //顶点（事件）的最晚发生时间
        int[] vertexLate = new int[vertexNum];
        calcVertexLate(vertexLate, vertexEarly);

        //计算各个边是否为关键路径
        calcPath(vertexEarly, vertexLate);
    }

    private void calcVertexEarly(int[] vertexEarly) {
        //顶点依赖的顶点列表，即事件依赖的活动
        List<Vertex>[] dependentVertex = getDependentVertex();
        for (int i : sort) {
            int maxWeight = 0;
            for (Vertex vertex : dependentVertex[i]) {
                int sumWeight = vertexEarly[vertex.id] + vertex.adjacentWeight;
                //事件最早发生时间取依赖活动的最大值
                if (sumWeight > maxWeight) {
                    maxWeight = sumWeight;
                }
            }
            vertexEarly[i] = maxWeight;
        }
        System.out.println("vertexEarly " + Arrays.toString(vertexEarly));
    }

    private void calcVertexLate(int[] vertexLate, int[] vertexEarly) {
        //终点事件最晚完成时间等于最早开始时间，也就是整个流程的完成时间。前序事件都依赖此时间来计算各自的最晚完成时间。
        //相当于确定了最终完成时间，要倒推出各自的最晚开始时间。因此这里取拓扑排序后的最后一个顶点。
        int terminal = sort[vertexNum - 1];
        vertexLate[terminal] = vertexEarly[terminal];
        //由于是倒推，要逆序处理，且要排除终点顶点
        for (int i = vertexNum - 2; i > -1; i--) {
            int vertexId = sort[i];
            int minWeight = Integer.MAX_VALUE;
            for (Vertex vertex : graph[vertexId]) {
                int newWeight = vertexLate[vertex.adjacentId] - vertex.adjacentWeight;
                //事件最晚发生时间取后续事件中的最晚发生时间减去活动时间后的最小值
                if (newWeight < minWeight) {
                    minWeight = newWeight;
                }
            }
            vertexLate[vertexId] = minWeight;
        }
        System.out.println("vertexLate  " + Arrays.toString(vertexLate));
    }

    private void calcPath(int[] vertexEarly, int[] vertexLate) {
        for (int i = 0; i < vertexNum; i++) {
            for (Vertex vertex : graph[i]) {
                //活动的最晚开始时间等于最早开始时间则为一条关键路径
                if (vertexLate[vertex.adjacentId] - vertex.adjacentWeight == vertexEarly[i]) {
                    System.out.println("critical path " + i + "->" + vertex.adjacentId);
                }
            }
        }
    }

    private List<Vertex>[] getDependentVertex() {
        //初始化各顶点依赖的顶点列表
        List<Vertex>[] dependentVertex = new ArrayList[vertexNum];
        for (int i = 0; i < vertexNum; i++) {
            dependentVertex[i] = new ArrayList<>();
        }
        for (int i = 0; i < vertexNum; i++) {
            for (Vertex vertex : graph[i]) {
                dependentVertex[vertex.adjacentId].add(vertex);
            }
        }
        print("[dependent vertex]", dependentVertex);
        return dependentVertex;
    }

    private void kahn() {
        int[] indegree = new int[vertexNum];
        for (int i = 0; i < vertexNum; i++) {
            for (Vertex vertex : graph[i]) {
                indegree[vertex.adjacentId]++;
            }
        }
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < vertexNum; i++) {
            if (indegree[i] == 0) {
                queue.add(i);
            }
        }
        sort = new int[vertexNum];
        int index = 0;
        while (!queue.isEmpty()) {
            int zero = queue.poll();
            sort[index] = zero;
            for (Vertex adjacent : graph[zero]) {
                indegree[adjacent.adjacentId]--;
                if (indegree[adjacent.adjacentId] == 0) {
                    queue.add(adjacent.adjacentId);
                }
            }
            index++;
        }
        if (index < vertexNum) {
            throw new RuntimeException("cycle in the graph!");
        }
        System.out.println("topological sort " + Arrays.toString(sort));
    }

    public void initDemo() {
        vertexNum = 9;
        graph = new ArrayList[vertexNum];
        for (int i = 0; i < vertexNum; i++) {
            graph[i] = new ArrayList<>();
        }
        addEdge(0, 1, 6);
        addEdge(0, 2, 4);
        addEdge(0, 3, 5);
        addEdge(1, 4, 1);
        addEdge(2, 4, 1);
        addEdge(3, 5, 2);
        addEdge(4, 6, 9);
        addEdge(4, 8, 7);
        addEdge(5, 8, 4);
        addEdge(6, 7, 2);
        addEdge(8, 7, 4);
        print("[graph]", graph);
    }

    private void print(String title, List<Vertex>[] list) {
        System.out.println(title);
        int index = 0;
        for (List<Vertex> arrayList : list) {
            System.out.println(index + " " + arrayList);
            index++;
        }
    }

    private void addEdge(int id, int adjacentId, int adjacentWeight) {
        graph[id].add(new Vertex(id, adjacentId, adjacentWeight));
    }

    private static class Vertex {
        private final int id;
        private final int adjacentId;
        private final int adjacentWeight;

        public Vertex(int id, int adjacentId, int adjacentWeight) {
            this.id = id;
            this.adjacentId = adjacentId;
            this.adjacentWeight = adjacentWeight;
        }

        @Override
        public String toString() {
            return "{" + "id=" + id + ", adjacentWeight=" + adjacentWeight + ", adjacentId=" + adjacentId + '}';
        }
    }
}

输出

[graph]
0 [{id=0, adjacentWeight=6, adjacentId=1}, {id=0, adjacentWeight=4, adjacentId=2}, {id=0, adjacentWeight=5, adjacentId=3}]
1 [{id=1, adjacentWeight=1, adjacentId=4}]
2 [{id=2, adjacentWeight=1, adjacentId=4}]
3 [{id=3, adjacentWeight=2, adjacentId=5}]
4 [{id=4, adjacentWeight=9, adjacentId=6}, {id=4, adjacentWeight=7, adjacentId=8}]
5 [{id=5, adjacentWeight=4, adjacentId=8}]
6 [{id=6, adjacentWeight=2, adjacentId=7}]
7 []
8 [{id=8, adjacentWeight=4, adjacentId=7}]
topological sort [0, 1, 2, 3, 4, 5, 6, 8, 7]
[dependent vertex]
0 []
1 [{id=0, adjacentWeight=6, adjacentId=1}]
2 [{id=0, adjacentWeight=4, adjacentId=2}]
3 [{id=0, adjacentWeight=5, adjacentId=3}]
4 [{id=1, adjacentWeight=1, adjacentId=4}, {id=2, adjacentWeight=1, adjacentId=4}]
5 [{id=3, adjacentWeight=2, adjacentId=5}]
6 [{id=4, adjacentWeight=9, adjacentId=6}]
7 [{id=6, adjacentWeight=2, adjacentId=7}, {id=8, adjacentWeight=4, adjacentId=7}]
8 [{id=4, adjacentWeight=7, adjacentId=8}, {id=5, adjacentWeight=4, adjacentId=8}]
vertexEarly [0, 6, 4, 5, 7, 7, 16, 18, 14]
vertexLate  [0, 6, 6, 8, 7, 10, 16, 18, 14]
critical path 0->1
critical path 1->4
critical path 4->6
critical path 4->8
critical path 6->7
critical path 8->7

生成的关键路径如图-4中的红线部分。

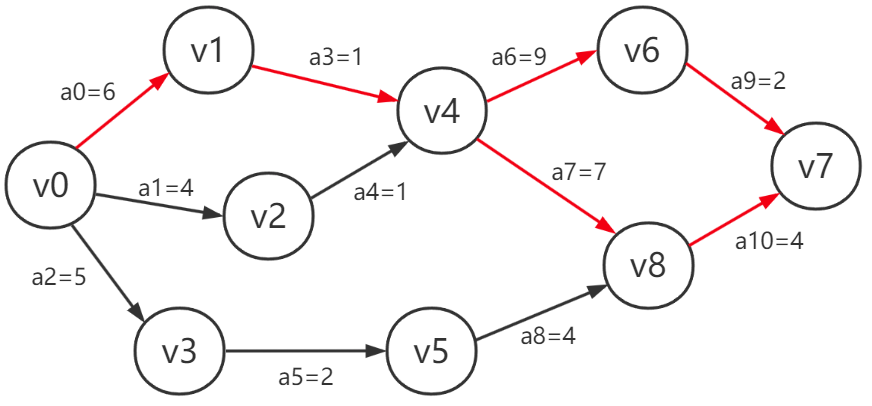
                                                                    图-4

关键路径有可能是某个顶点的多条后驱边。如图中v4对应的的a6、a7都是关键路径，是因为v4-v7途径的两条路径累计消耗时间相等导致的。这种是符合预期的。

 

总结

我们通过给图增加权重配合拓扑排序，再根据最早发生时间等于最晚发生时间这个特性，计算出关键路径。

关键路径上对应的活动即为关键活动，是不能延期的。如果想提前完成项目，则要减少关键活动的花费时间。当减少某个关键活动花费时间后可能导致此活动不再是关键活动，就需要重新计算关键路径。

 

参考资料

关键路径-视频