拓扑排序
日常项目开发中,一般流程是产品经理提出需求,相关人员进行需求评审,然后是前后端工程师开发功能,再到测试、发布上线。
流程如下:
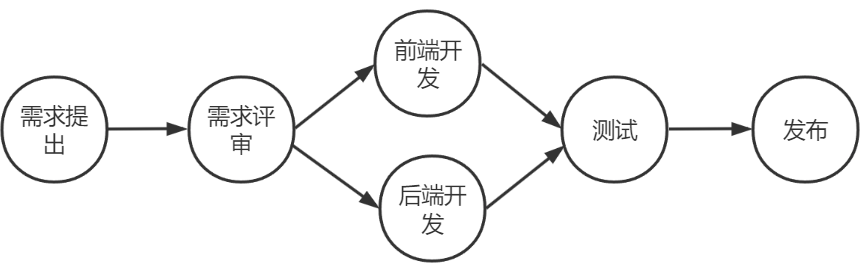
图-1
可以看到,这些步骤是存在先后(依赖)关系的:前后端的开发依赖于需求评审,测试又依赖前后端开发。不可能需求还没评审,工程师就开始开发。
其次,这些步骤之间不能存在相互依赖,例如需求评审又依赖测试,这样就没法执行下去了。

图-2
我们把满足这些特性的流程称为AOV网(Activity On Vertex Network),步骤可以看作是一个个活动(activity),用图的顶点(vertex)来表示。对应到图的数据结构,是一张带有方向的且无环(无相互依赖)的有向无环图(Directed Acyclic Graph),简称DAG。
* AOE网是用边来表示活动(Activity On Edge Network)
根据这种有向无环图(DAG)生成的各顶点(活动)的依赖序列,我们称为拓扑排序(Topologial Sort)。
可以看到这里的排序是基于依赖关系的,不同于之前介绍的冒泡、快速排序等这种基于大小的排序。而拓扑的意思,根据Kahn发表的“Topological Sorting of Large Networks”一文,应该是解决计算机网络结构中的“拓扑”,倾向于计算机网络中表示各个网络节点关系的拓扑图。
下面介绍两种拓扑排序的算法
一、卡恩算法(Kahn's algorithm)
该方法理解起来比较简单,主要流程是先计算出每个顶点依赖的顶点个数,或者叫顶点的入度(indegree),从没有依赖其他顶点的顶点a(即入度为0的顶点)开始处理,处理完毕同时把依赖此顶点a的对应顶点数量减一。之后再计算出一个没有依赖的顶点,再把对应顶点数量减一,直到处理完全部顶点。
二、深度优先搜索(Depth First Search)
深度优先搜索只是一个单纯的遍历,怎么会满足拓扑排序呢?我们先回顾下深度优先搜索的流程,如图-3
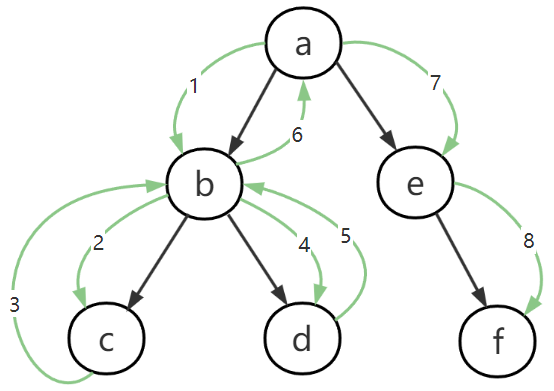
图-3
可以看到深度优先是优先往一条路径的深层搜索,当到达最底层顶点c后,再回到上一层b,访问b对应的d,之后再回到b,由于b对应的顶点都已经访问过,则回溯至a,a还有未访问的顶点e,e再下探至f。第一次到达最底层的顶点c,一定是此路径的终点,从依赖的角度看,必然为依赖的最后一步。当本层顶点全部遍历完毕后,才会回到上层顶点,相当于以上层顶点为依赖的顶点已经遍历完成。如图-3中,b指向的c d,即c d依赖b。按照c d b访问顺序存储,再按照倒序的b d c输出,就实现了依赖的排序。
可见实现了图的深度优先搜索,也就得到了拓扑排序的结果。不过要优先保存最底层的顶点,且需要考虑环的问题。
以下为两种算法的实现代码和输出说明,演示图数据如下。
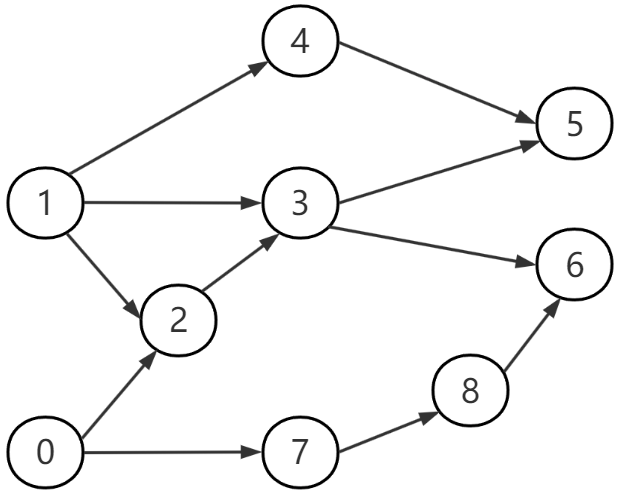
图-4
图-4演示数据参考于https://www.bilibili.com/video/BV1uf4y1U7DX
1 import java.util.*; 2 3 public class TopologicalSort { 4 private int vertexNum; 5 private List<Integer>[] graph; 6 7 private boolean[] visited; 8 private boolean[] search; 9 private Stack<Integer> dfsSort; 10 11 public static void main(String[] args) { 12 TopologicalSort tsk = new TopologicalSort(); 13 tsk.initDemo(); 14 tsk.print(); 15 16 System.out.println("[Kahn]"); 17 tsk.kahn(); 18 System.out.println("[DFS]"); 19 tsk.dfs(); 20 } 21 22 public void kahn() { 23 //计算每个顶点的入度(即指向此顶点的边的数量,也就是依赖的顶点数) 24 int[] indegree = new int[vertexNum]; 25 for (int i = 0; i < vertexNum; i++) { 26 for (int vertex : graph[i]) { 27 indegree[vertex]++; 28 } 29 } 30 //初始入度为0的顶点 31 Queue<Integer> queue = new LinkedList<>(); 32 for (int i = 0; i < vertexNum; i++) { 33 if (indegree[i] == 0) { 34 queue.add(i); 35 } 36 } 37 System.out.println("indegree " + Arrays.toString(indegree) + " queue " + queue); 38 39 //排序结果 40 List<Integer> sort = new ArrayList<>(); 41 while (!queue.isEmpty()) { 42 //取出一个入度为0的顶点 43 int zero = queue.poll(); 44 //并保存到排序结果中 45 sort.add(zero); 46 System.out.println("zero " + zero + " adjacent " + graph[zero]); 47 //依赖此顶点的顶点入度减一(即以此顶点开始的边) 48 for (int adjacent : graph[zero]) { 49 indegree[adjacent]--; 50 if (indegree[adjacent] == 0) { 51 System.out.println("enqueue <- " + adjacent); 52 queue.add(adjacent); 53 } 54 } 55 System.out.println("indegree " + Arrays.toString(indegree) + " queue " + queue); 56 } 57 //排序结果集个数小于顶点数量,说明存在环(即顶点的入度都大于0) 58 if (sort.size() < vertexNum) { 59 System.out.println("cycle in the graph!"); 60 } else { 61 System.out.println(sort); 62 } 63 } 64 65 public void dfs() { 66 //保存顶点是否访问过 67 visited = new boolean[vertexNum]; 68 //保存顶点是否正在搜索,用于环的判断 69 search = new boolean[vertexNum]; 70 //排序结果 71 dfsSort = new Stack<>(); 72 73 //顶点依次遍历 74 for (int v = 0; v < vertexNum; v++) { 75 if (!visited[v]) { 76 traversal(v); 77 } 78 } 79 //排序结果输出 80 while (!dfsSort.empty()) { 81 System.out.print(dfsSort.pop() + " "); 82 } 83 } 84 85 private void traversal(int vertex) { 86 //标记为已访问 87 visited[vertex] = true; 88 //标记为搜索中 89 search[vertex] = true; 90 System.out.printf("%s start-> adjacent %s visited %s dfsSort %s search %s\n", vertex, graph[vertex], Arrays.toString(visited), dfsSort, Arrays.toString(search)); 91 92 for (int i : graph[vertex]) { 93 //环的存在会导致顶点处于搜索状态时再次搜索 94 if (search[i]) { 95 throw new RuntimeException("vertex " + i + ", cycle in the graph!"); 96 } 97 if (!visited[i]) { 98 traversal(i); 99 } else { 100 System.out.println("skip " + i); 101 } 102 } 103 //标记为搜索结束 104 search[vertex] = false; 105 //搜索结束同时添加到结果集 106 dfsSort.add(vertex); 107 System.out.printf("%s <-end adjacent %s visited %s dfsSort %s search %s\n", vertex, graph[vertex], Arrays.toString(visited), dfsSort, Arrays.toString(search)); 108 } 109 110 public void print() { 111 System.out.println("[graph]"); 112 int index = 0; 113 for (List<Integer> arrayList : graph) { 114 System.out.println(index + " " + arrayList); 115 index++; 116 } 117 } 118 119 public void initDemo() { 120 this.vertexNum = 9; 121 graph = new ArrayList[vertexNum]; 122 for (int i = 0; i < vertexNum; i++) { 123 graph[i] = new ArrayList<>(); 124 } 125 addEdge(0, 2, 7); 126 addEdge(1, 2, 3, 4); 127 addEdge(2, 3); 128 addEdge(3, 5, 6); 129 addEdge(4, 5); 130 addEdge(7, 8); 131 addEdge(8, 6); 132 //cyclic 133 //addEdge(5, 1); 134 } 135 136 private void addEdge(int a, int... b) { 137 for (int i : b) { 138 graph[a].add(i); 139 } 140 } 141 }
输出
[graph] 0 [2, 7] 1 [2, 3, 4] 2 [3] 3 [5, 6] 4 [5] 5 [] 6 [] 7 [8] 8 [6] [Kahn] indegree [0, 0, 2, 2, 1, 2, 2, 1, 1] queue [0, 1] zero 0 adjacent [2, 7] enqueue <- 7 indegree [0, 0, 1, 2, 1, 2, 2, 0, 1] queue [1, 7] zero 1 adjacent [2, 3, 4] enqueue <- 2 enqueue <- 4 indegree [0, 0, 0, 1, 0, 2, 2, 0, 1] queue [7, 2, 4] zero 7 adjacent [8] enqueue <- 8 indegree [0, 0, 0, 1, 0, 2, 2, 0, 0] queue [2, 4, 8] zero 2 adjacent [3] enqueue <- 3 indegree [0, 0, 0, 0, 0, 2, 2, 0, 0] queue [4, 8, 3] zero 4 adjacent [5] indegree [0, 0, 0, 0, 0, 1, 2, 0, 0] queue [8, 3] zero 8 adjacent [6] indegree [0, 0, 0, 0, 0, 1, 1, 0, 0] queue [3] zero 3 adjacent [5, 6] enqueue <- 5 enqueue <- 6 indegree [0, 0, 0, 0, 0, 0, 0, 0, 0] queue [5, 6] zero 5 adjacent [] indegree [0, 0, 0, 0, 0, 0, 0, 0, 0] queue [6] zero 6 adjacent [] indegree [0, 0, 0, 0, 0, 0, 0, 0, 0] queue [] [0, 1, 7, 2, 4, 8, 3, 5, 6] [DFS] 0 start-> adjacent [2, 7] visited [true, false, false, false, false, false, false, false, false] dfsSort [] search [true, false, false, false, false, false, false, false, false] 2 start-> adjacent [3] visited [true, false, true, false, false, false, false, false, false] dfsSort [] search [true, false, true, false, false, false, false, false, false] 3 start-> adjacent [5, 6] visited [true, false, true, true, false, false, false, false, false] dfsSort [] search [true, false, true, true, false, false, false, false, false] 5 start-> adjacent [] visited [true, false, true, true, false, true, false, false, false] dfsSort [] search [true, false, true, true, false, true, false, false, false] 5 <-end adjacent [] visited [true, false, true, true, false, true, false, false, false] dfsSort [5] search [true, false, true, true, false, false, false, false, false] 6 start-> adjacent [] visited [true, false, true, true, false, true, true, false, false] dfsSort [5] search [true, false, true, true, false, false, true, false, false] 6 <-end adjacent [] visited [true, false, true, true, false, true, true, false, false] dfsSort [5, 6] search [true, false, true, true, false, false, false, false, false] 3 <-end adjacent [5, 6] visited [true, false, true, true, false, true, true, false, false] dfsSort [5, 6, 3] search [true, false, true, false, false, false, false, false, false] 2 <-end adjacent [3] visited [true, false, true, true, false, true, true, false, false] dfsSort [5, 6, 3, 2] search [true, false, false, false, false, false, false, false, false] 7 start-> adjacent [8] visited [true, false, true, true, false, true, true, true, false] dfsSort [5, 6, 3, 2] search [true, false, false, false, false, false, false, true, false] 8 start-> adjacent [6] visited [true, false, true, true, false, true, true, true, true] dfsSort [5, 6, 3, 2] search [true, false, false, false, false, false, false, true, true] skip 6 8 <-end adjacent [6] visited [true, false, true, true, false, true, true, true, true] dfsSort [5, 6, 3, 2, 8] search [true, false, false, false, false, false, false, true, false] 7 <-end adjacent [8] visited [true, false, true, true, false, true, true, true, true] dfsSort [5, 6, 3, 2, 8, 7] search [true, false, false, false, false, false, false, false, false] 0 <-end adjacent [2, 7] visited [true, false, true, true, false, true, true, true, true] dfsSort [5, 6, 3, 2, 8, 7, 0] search [false, false, false, false, false, false, false, false, false] 1 start-> adjacent [2, 3, 4] visited [true, true, true, true, false, true, true, true, true] dfsSort [5, 6, 3, 2, 8, 7, 0] search [false, true, false, false, false, false, false, false, false] skip 2 skip 3 4 start-> adjacent [5] visited [true, true, true, true, true, true, true, true, true] dfsSort [5, 6, 3, 2, 8, 7, 0] search [false, true, false, false, true, false, false, false, false] skip 5 4 <-end adjacent [5] visited [true, true, true, true, true, true, true, true, true] dfsSort [5, 6, 3, 2, 8, 7, 0, 4] search [false, true, false, false, false, false, false, false, false] 1 <-end adjacent [2, 3, 4] visited [true, true, true, true, true, true, true, true, true] dfsSort [5, 6, 3, 2, 8, 7, 0, 4, 1] search [false, false, false, false, false, false, false, false, false] 1 4 0 7 8 2 3 6 5
卡恩算法示意图-5

图-5
深度优先搜索算法示意图-6
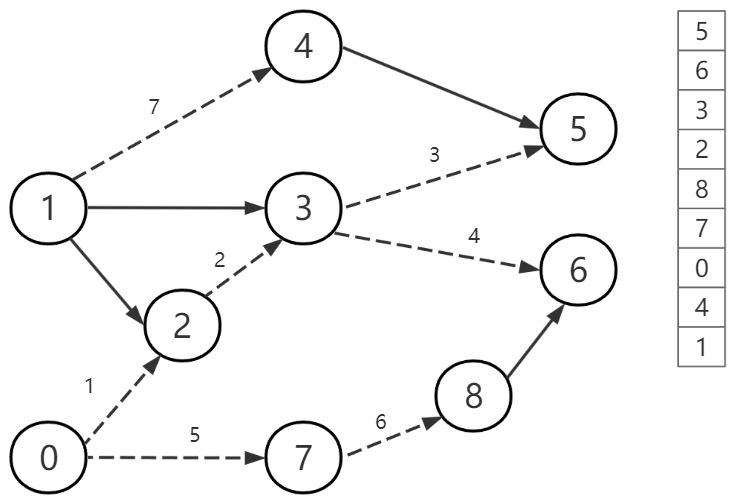
图-6
可以看到两种算法对环的检测机制是不同的,卡恩算法是通过计算每个顶点的入度,入度为0即不存在依赖,如果最终仍然存在入度不是0的节点,必然存在环。
深度优先搜索算法中,由于是递归调用,顶点开始搜索时把状态标记为搜索中,一直到本次递归结束后才会更新为搜索结束,遍历期间如果这个开始顶点再次出现,则说明必然存在环。
如图-7,当顶点1开始后被标记为搜索中,到达4,再到达5,而5存在指向1的边,再到达顶点1时,发现1的状态已经是搜索中了,说明这里出现了环。也就是我们需要区分出正常的回溯和环导致的重新访问。
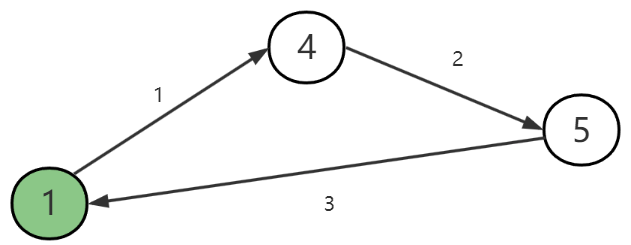
图-7
递归方式(代码的98行traversal方法)乍一看可能不太容易理解,看一下算法的输出内容图-8就很容易明白了,这里我增加了缩进,方便观察层次关系。可以认为是大循环里套了小循环,等小循环完毕大循环才能结束。0可以认为是最外侧的大循环,里面又开始了2、7,2里面又开始了3,3里面又开始了5、6……但不管小循环如何再嵌套,只有全部完成后大循环才能结束。

图-8
拓扑的扩展阅读
参考资料


 浙公网安备 33010602011771号
浙公网安备 33010602011771号