并查集

之前在介绍“图的一些基本概念”中提到了最小生成树，其中一种算法是克鲁斯卡尔（Kruskal's algorithm）算法，里面涉及了对环的判断。我们再回顾下算法的主要流程：

从最小的一个边开始连接，然后再连接第二小的边，且保证新加入的边不能和已经连接的顶点形成环。这样一直重复，最终连接起所有的顶点。

算法中提到的“形成环”是指新加入的边导致图形成了一个回路。类似图示这种结构，新加入的b-c边导致a b c顶点边构成了一个回路

                  图-1

如果从树的角度来看，即b和c的拥有同一个根节点a。如果层级多一些，类似如下

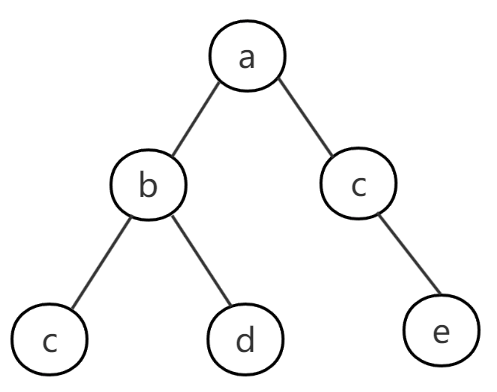
                            图-2

c e也拥有同一个根节点a。因此我们可以通过判断两个节点是否具有相同的根节点，来判断是否属于同一棵树，我们把这种操作叫做查询（find）。

由于算法是从最小边开始逐渐连接各个边的，不一定能保证新加入的边和之前边是相连的。如图这种情况，a-b和c-e这两个边在某个中间状态可能是分开的。

                              图-3

但最终的最小生成树必然要连接起各个顶点，也就必然要连接相应的边，我们把这种连接操作称为合并（union）。

有了查询和合并的这两个定义，我们再看并查集就很容易明白了。

所谓并查集（union-find set或者disjoint set）是用来查找元素和合并集合的一种数据类型。是对关系的处理，用来合并集合，确定元素是否属于某个集合。

示例中树结构可以理解成集合的一种具体表现形式。在图-2中，a-c c-e我们能推导出a-e也是连接的，只不过中间经过了c。连接也只是一种统称，具体形式可以是亲戚朋友关系、道路或电路连通等，都是对关系的一种表述。

 

接下来我们看下具体的数据结构和实现方法。先实现基础的查询和合并，再一步步完善。为了方便演示，我们假定有0-9共计10个节点，分别对应数组的下标0-9。每个数组值默认也是0-9，表示根节点是自身。

                                                   图-4

public class UnionFindSetV1 {
    private final int[] parent;

    public static void main(String[] args) {
        UnionFindSetV1 ufs = new UnionFindSetV1(10);
        System.out.println(Arrays.toString(ufs.parent));
        ufs.union(0, 1);
        ufs.union(1, 2);
        ufs.union(2, 3);
        ufs.union(8, 9);
        System.out.println(Arrays.toString(ufs.parent));
        System.out.println("1 root: " + ufs.find(1));
        System.out.println("2 root: " + ufs.find(2));
    }

    public UnionFindSetV1(int num) {
        parent = new int[num];
        for (int i = 0; i < num; i++) {
            //根节点初始化为自身
            parent[i] = i;
        }
    }

    public int find(int i) {
        //值等于自身说明是根节点
        if (parent[i] == i) {
            return i;
        }
        //递归查询所属的根节点
        return find(parent[i]);
    }

    public void union(int i, int j) {
        int a = find(i);
        int b = find(j);
        //属于同一个根节点无需操作
        if (a == b) {
            return;
        }
        //后一个元素的根节点设置为第一个元素
        parent[j] = i;
    }
}

 输出

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 0, 1, 2, 4, 5, 6, 7, 8, 8]
1 root: 0
2 root: 0

从代码中可以看到，我们对节点(0, 1) (1, 2) (2, 3) (8, 9)分别执行了合并操作，这里规定了第一个元素当做根节点。在进行合并操作的时候，先查找两个元素所属的根节点，如果属于同一个根节点说明属于同一个集合，无需操作。否则直接把第二个元素的根节点更新为第一个元素。执行完毕，对应的数组和树的结构如下

                                                                 图-5

 

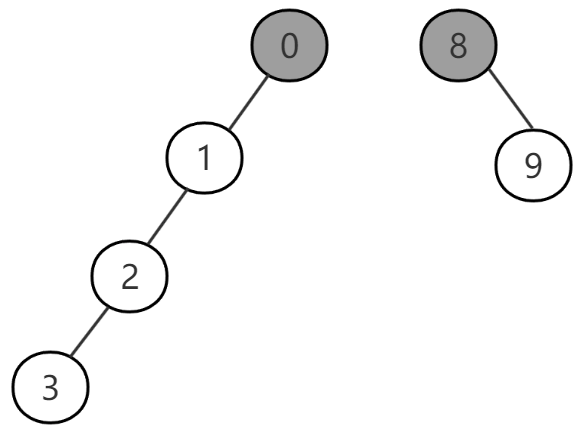
                                    图-6 

执行查找操作时，先找到该元素的父节点，再查找父节点的父节点，直到发现父节点是自身值时。节点1和2的查找过程示意图如下，可以看到1只查找了一次，2则先找到1，再从1找到了0。

                  图-7

从查找根节点的操作过程中，我们不难发现随着节点不断连接，会导致树的高度不断增长，这样后续节点查找所属根节点时，导致查找步骤越来越多。例如连接(2, 3)后，当查找3的根节点时，步骤必然会加一。

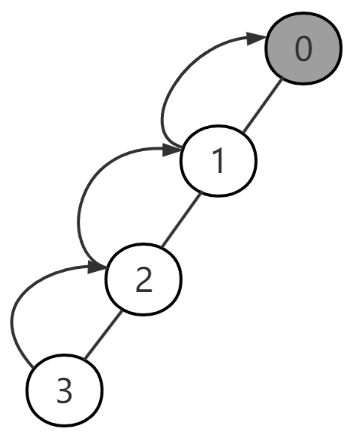
                图-8

因此我们考虑如何减少树的高度。一种理想的情况是每个节点都直接存储它的根节点，也就是如下格式。

                     

                      图-9                                                                                                       图-10

如何让节点存储它的最终根节点呢？我们观察下find方法，其实执行此方法时，由于是递归调用是知道最终的根节点的，这里就可以修改为最终的根节点，这样后续再次查找时就可以直接取到最终的根节点了。把find方法调整为如下：

public int find(int i) {
    //值等于自身说明是根节点
    if (parent[i] == i) {
        return i;
    }
    //递归查询所属的根节点，并把当前节点的根节点设置为查询到的最终根节点
    parent[i] = find(parent[i]);
    return parent[i];
}

同时调整下main方法的测试代码，增加

System.out.println("3 root: " + ufs.find(3));
System.out.println(Arrays.toString(ufs.parent));

最终输出

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 0, 0, 2, 4, 5, 6, 7, 8, 8]
1 root: 0
2 root: 0
3 root: 0
[0, 0, 0, 0, 4, 5, 6, 7, 8, 8]  #这里3的根节点已经被修改为0

我们把这种减少查找根节点步骤的操作称为路径压缩（path compression）

有了路径压缩，我们再看下合并操作是否有优化空间。 看下图-11这种情况，其实是有两种合并方法的，一种是8做根节点，另一种是7做根节点。虽然两种方法都实现了集合的合并，但方法1的高度是小于方法2的。而高度的增加会导致查询次数变多。

 

                                                       图-11

因此我们可以考虑记录每棵子树的高度，优先用高度较大的树当根节点，从而保证合并后的树高度维持不变。我们把这种方法称为按高度合并（union-by-height），或者按秩（rank）合并。对应代码中，需要引入一个记录高度信息的height数组，每个元素对应的初始高度为1。具体代码如下：

public class UnionFindSetV3 {
    private final int[] parent;
    private final int[] height;

    public static void main(String[] args) {
        UnionFindSetV3 ufs = new UnionFindSetV3(10);
        System.out.println(Arrays.toString(ufs.parent) + " height " + Arrays.toString(ufs.height));
        ufs.union(0, 1);
        System.out.println("0-1 " + Arrays.toString(ufs.parent) + " height " + Arrays.toString(ufs.height));
        ufs.union(2, 0);
        System.out.println("2-0 " + Arrays.toString(ufs.parent) + " height " + Arrays.toString(ufs.height));
    }

    public UnionFindSetV3(int num) {
        parent = new int[num];
        height = new int[num];
        for (int i = 0; i < num; i++) {
            //根节点初始化为自身
            parent[i] = i;
            //高度默认为1
            height[i] = 1;
        }
    }

    public int find(int i) {
        //值等于自身说明是根节点
        if (parent[i] == i) {
            return i;
        }
        //递归查询所属的根节点，并把当前节点的根节点设置为查询到的最终根节点
        parent[i] = find(parent[i]);
        return parent[i];
    }

    public void union(int i, int j) {
        int a = find(i);
        int b = find(j);
        //属于同一个根节点无需操作
        if (a == b) {
            return;
        }
        if (height[j] > height[i]) {
            //高度大的做为根节点，且合并后高度不变
            parent[i] = j;
        } else {
            parent[j] = i;
            if (height[i] == height[j]) {
                //高度相等时的合并会导致高度加1
                height[i]++;
            }
        }
    }
}

 输出

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9] height [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
0-1 [0, 0, 2, 3, 4, 5, 6, 7, 8, 9] height [2, 1, 1, 1, 1, 1, 1, 1, 1, 1] #元素1对应的根节点是0，由于合并前0、1高度都是1，导致合并后0的高度变为2
2-0 [0, 0, 0, 3, 4, 5, 6, 7, 8, 9] height [2, 1, 1, 1, 1, 1, 1, 1, 1, 1] #当无高度判断时，仅以出现顺序为依据，默认2为根节点。当增加对高度判断后，元素0对应的高度2，大于元素2的高度0，因此以高度较大的0为根节点，合并后0的高度仍然是2。

 

总结

我们从克鲁斯卡尔算法引出了“并查集”的概念，并且基于数组结构实现了快速判断集合中两个元素间的关系（是否属于同一个根节点），同时也支持动态合并集合。另外为提升查询效率引入“路径压缩”的方法，减少了查询根节点的次数。在集合合并时又引入“按高度合并”的操作，降低了合并后树的高度。通过这些介绍，相信大家（我）对并查集会有更深地理解。

 

参考资料

Disjoint Set Union (Union Find) 

并查集入门-视频

数据结构与算法分析：Java语言描述（原书第3版）第八章-不相交集类