最短路径算法之——Floyd算法介绍与实现

之前我们学习了图的最短路径算法之Dijkstra算法，知道此算法是用来求指定的两顶点间最短路径的（也称单源最短路径single-source），如果要求图中任意两顶点间的最短路径，怎么办呢？

当然可以通过对任意两点调用Dijkstra算法来实现。有没有更好的办法，运行一次就能求解出任意两顶点的距离呢？

这里我们介绍下Floyd算法（Floyd–Warshall、Roy–Warshall、Roy–Floyd都指同一种算法），就是专门用来求解此问题的。

我们先看下该算法的基本思想。如图示，我们有三个顶点 a b c

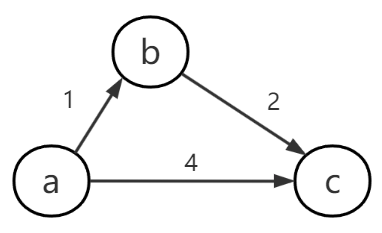
顶点a到c的直达路径为a-c，距离为4。为了探索其它更短路径，我们选择一个新的顶点b，看b是否能缩短a-c的距离，得知a-b距离为1，b-c距离为2， 1+2<4，说明经过b点是可以缩短距离的，即a-c的更短的距离等于a-b距离加上b-c的距离。

可以看到通过引入新的顶点，达到了缩短原有路程的目的。新的顶点我们可以理解为排除开始和结束两顶点，其他顶点的统称，通过依次引入这些顶点，判断开始点到此顶点距离加上此顶点到结束点的距离，如果小于开始和顶点间的原始距离，则更新为这个距离。

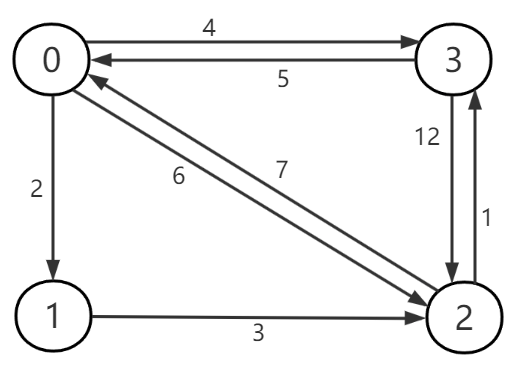
接下来我们就按照这个思路来编写代码。演示图顶点信息如下

代码

public class Floyd {
    private static final int MAX_WEIGHT = 999;
    private static final int NOT_EXISTS_PATH = -1;

    public static void main(String[] args) {
        //顶点个数
        int vertexNum = 4;
        //顶点数据
        int[][] vertices = initVertex(vertexNum);
        //路径默认数据
        int[][] path = initPath(vertices);
        print(vertices, "vertex");
        print(path, "path");

        //midVertex为中间顶点，判断加入此顶点后能否缩短原有距离。例如a至b的距离，则转换为a至midVertex距离加上midVertex至b的距离。
        //每个顶点都需要做一次中间顶点，所以最外层为中间顶点
        for (int midVertex = 0; midVertex < vertexNum; midVertex++) {
            //顶点要两两判断，这样才能求解任意两个顶点的距离，因此是一个两层循环
            for (int i = 0; i < vertexNum; i++) {
                for (int j = 0; j < vertexNum; j++) {
                    //i到j距离，对比i到midVertex距离加上midVertex到j的距离，小于则更新为这个midVertex顶点
                    if (vertices[i][j] > vertices[i][midVertex] + vertices[midVertex][j]) {
                        System.out.printf("midVertex %d %d-%d dist=%d>%d+%d ", midVertex, i, j, vertices[i][j], vertices[i][midVertex], vertices[midVertex][j]);
                        vertices[i][j] = vertices[i][midVertex] + vertices[midVertex][j];
                        System.out.printf("path=%d\n", path[midVertex][j]);
                        //注意！直接前驱顶点不能直接设置为midVertex，而是取midVertex到结束顶点j的直接前驱顶点
                        path[i][j] = path[midVertex][j];
                    }
                }
            }
        }

        print(vertices, "vertex");
        print(path, "path");
        //顶点3到2的最短路径经过的各个边
        printShortestPath(3, 2, path);
    }

    private static void printShortestPath(int i, int j, int[][] path) {
        System.out.printf("[path %d-%d]\n", i, j);
        while (path[i][j] != NOT_EXISTS_PATH) {
            System.out.printf("%d->%d\n", path[i][j], j);
            j = path[i][j];
        }
    }

    private static int[][] initVertex(int vertexNum) {
        int[][] vertex = new int[vertexNum][vertexNum];
        for (int i = 0; i < vertexNum; i++) {
            for (int j = 0; j < vertexNum; j++) {
                if (i == j) {
                    vertex[i][i] = 0;
                } else {
                    vertex[i][j] = MAX_WEIGHT;
                }
            }
        }
        vertex[0][1] = 2;
        vertex[0][2] = 6;
        vertex[0][3] = 4;

        vertex[1][2] = 3;

        vertex[2][0] = 7;
        vertex[2][3] = 1;

        vertex[3][0] = 5;
        vertex[3][2] = 12;
        return vertex;
    }

    private static int[][] initPath(int[][] vertices) {
        int[][] path = new int[vertices.length][vertices.length];
        for (int i = 0; i < vertices.length; i++) {
            for (int j = 0; j < vertices.length; j++) {
                if (vertices[i][j] != MAX_WEIGHT && i != j) {
                    path[i][j] = i;
                } else {
                    path[i][j] = NOT_EXISTS_PATH;
                }
            }
        }
        return path;
    }

    private static void print(int[][] vertices, String name) {
        System.out.printf("[%s]\n", name);
        System.out.print("+   ");
        for (int i = 0; i < vertices.length; i++) {
            System.out.printf("%d   ", i);
        }
        System.out.println();
        int index = 0;
        for (int[] ints : vertices) {
            System.out.printf("%d  ", index++);
            for (int j = 0; j < vertices.length; j++) {
                if (ints[j] == MAX_WEIGHT) {
                    System.out.print(" -  ");
                } else {
                    System.out.printf("%2d  ", ints[j]);
                }
            }
            System.out.println();
        }
    }
}

输出

[vertex] #顶点信息，第一行、第一列都为下标数据方便数据查看。“-”为无穷大（内部用的999表示），可以认为是两个顶点间无直接路径
+   0   1   2   3   
0   0   2   6   4  
1   -   0   3   -  
2   7   -   0   1  
3   5   -  12   0  
[path]  #默认的各顶点直接前驱的顶点， -1为此路径不存在，即不存在前驱
+   0   1   2   3   
0  -1   0   0   0  
1  -1  -1   1  -1  
2   2  -1  -1   2  
3   3  -1   3  -1  
midVertex 0 2-1 dist=999>7+2 path=0  #以顶点0为中间顶点，判断0的引入是否能缩短2-1间的路径，因为2-1没有直接路径相连，默认为无穷大，2-0长度为7，0-1长度为2，7+2小于无穷大（999），因此把2-1路径长度改为9，同时把顶点1的前驱改为顶点0
midVertex 0 3-1 dist=999>5+2 path=0  #同上判断3-0，0-1，相加后为7，小于无穷大，更新，同时把顶点1的直接前驱改为顶点0
midVertex 0 3-2 dist=12>5+6 path=0
midVertex 1 0-2 dist=6>2+3 path=1
midVertex 1 3-2 dist=11>7+3 path=1
midVertex 2 1-0 dist=999>3+7 path=2
midVertex 2 1-3 dist=999>3+1 path=2
midVertex 3 1-0 dist=10>4+5 path=3
midVertex 3 2-0 dist=7>1+5 path=3
midVertex 3 2-1 dist=9>1+7 path=0  #顶点1的直接前驱顶点改为0，注意这个0是中间顶点3-1对应的直接前驱顶点0
[vertex]  #最终各个顶点间的最短路径
+   0   1   2   3   
0   0   2   5   4  
1   9   0   3   4  
2   6   8   0   1  
3   5   7  10   0  
[path]  #各顶点的直接前驱顶点
+   0   1   2   3   
0  -1   0   1   0  
1   3  -1   1   2  
2   3   0  -1   2  
3   3   0   1  -1  
[path 3-2]  #顶点3到2最短路径经过的边
1->2
0->1
3->0

可以看到Floyd算法的代码是相当简练的：最外层为要引入的中间顶点，即判断这个顶点的加入是否能缩短任意两个顶点间的距离，而任意一个顶点都可以当做中间顶点，再加上任意两个顶点的组合（两层循环），就构成了一个三层的循环。因此随着顶点数量的增多，循环的次数增长较快（假设顶点个数为N，则对应的循环次数为N*N*N=N³）。

参考资料
https://baike.baidu.com/item/Floyd%E7%AE%97%E6%B3%95/291990

https://brilliant.org/wiki/floyd-warshall-algorithm/

https://www.bilibili.com/video/BV1K5411f7G7

https://www.bilibili.com/video/BV1RK4y1d7ct