最短路径算法之——Dijkstra算法介绍与实现

我们使用导航应用时，选择好出发地和目的地，就能计算出两地的最短距离，而且能显示出到各个路口的距离。这个场景映射到数据结构和算法中，其实是求图中两个顶点间的最短距离。由于是从一个顶点到另外一个顶点，涉及到方向以及不同顶点间的距离，因此是带权重的有向图。

我们先大概分析下这个问题。

一般我们的想法是两顶点间直达的距离是最短的，但存在通过其他顶点“绕路”后反而距离更短的情况，例如求b到c点的最短路径时，经过a点再到c，反而优于b-c直达距离。

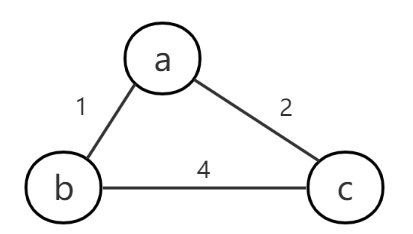
但即使这次绕路后是最短路径，再次绕路反而会更远。如下图求b到d最短路径，到达c点后选择直达的c-d反而更近。

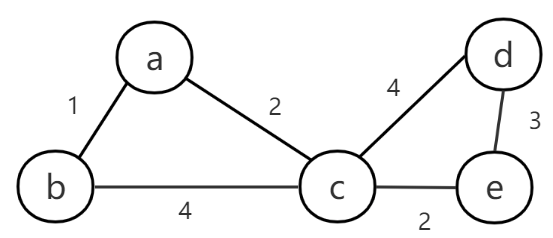
因此我们不能只根据当前的路径值来进行选择，需要记录从开始顶点到每个后续顶点的累计距离，如果后续有其他边再次经过该顶点时，则判断新的累计距离是否小于先前的累计距离，小于则更新为这个更小的累计距离，表示发现了更短的路径。

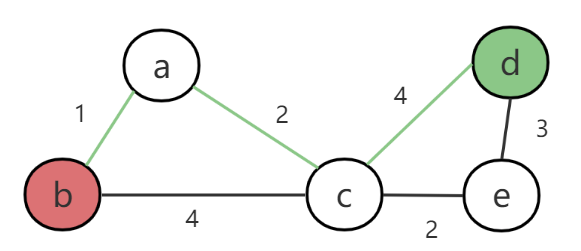
例如求b-d最短路径。从b点出发时，我们发现共有a c两条路可以选择，那么就把a标记为距离1，c标记为距离4。接下来再分别从a、c两点对应的路径继续计算。a点对应的是c，这时发现c点之前已经存在距离4，于是把a点的累计路径1加上a-c路径长度2，再和c先前的累计距离4对比，1+2=3<4，说明b-a-c这个路径距离是短于b-c路径的，于是把c点累计距离更新为3，这样就解决了之前的绕路问题，保证c顶点的累计距离必然是之前最短的路径之和。

同时，我们可以看出b-a-c-d最短路径中，c点如果是最短路径中必然经过的一个点，则b到c的最短路径b-a-c也必然包含在最终的最短路径中，这其实就是Dijkstra算法的基础。

                   引用自Edsger W. Dijkstra "A Note on Two Problems in Connexion with Graphs"

 

按照这个思路我们来编写代码。演示数据如图，求顶点0到顶点6的最短路径。

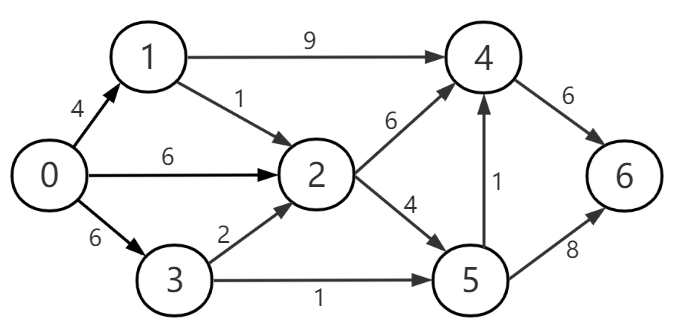
代码

import java.util.ArrayList;
import java.util.Arrays;

public class ShortestPath {
    private static final int MAX_WEIGHT = 999;
    private static final int NOT_EXISTS_PATH = -1;

    public static void main(String[] args) {
        //顶点个数
        int vertexNum = 7;
        //初始化演示数据
        ArrayList<Vertex>[] list = initDemo(vertexNum);
        print(list);

        //开始顶点
        int startVertex = 0;
        //结束顶点
        int endVertex = 6;

        //记录访问过的顶点，默认false。记录每次可选路径中对应路径最小的顶点
        boolean[] visit = new boolean[vertexNum];

        //记录每个顶点到前一个顶点的路径之和，默认为最大值。如果新的路径小于这个数，说明需要更新
        int[] dist = new int[vertexNum];
        Arrays.fill(dist, MAX_WEIGHT);

        //记录顶点对应的前一个顶点，用于还原最小路径
        int[] prev = new int[vertexNum];
        Arrays.fill(prev, NOT_EXISTS_PATH);

        //需要把开始顶点的路径和设置为0，这样才能保证首次选择的必然是开始顶点（其他顶点的路径和都是最大值）
        dist[startVertex] = 0;
        while (true) {
            //取未访问过的顶点中，最小路径和的顶点
            int minVertex = findMin(dist, visit);
            if (minVertex == NOT_EXISTS_PATH || minVertex == endVertex) {
                break;
            }
            visit[minVertex] = true;

            for (Vertex v : list[minVertex]) {
                //当前路径值加前一个顶点路径值，如果小于当前顶点的累计值，需要更新当前顶点的累计值
                if (!visit[v.id] && v.weight + dist[minVertex] < dist[v.id]) {
                    dist[v.id] = v.weight + dist[minVertex];
                    //更新路径为前一个顶点
                    prev[v.id] = minVertex;
                }
            }
            System.out.printf("minVertex %s dist %s visit %s prev %s\n", minVertex, Arrays.toString(dist), Arrays.toString(visit), Arrays.toString(prev));
        }

        //打印最终路径
        int prevVertex = endVertex;
        while (prev[prevVertex] != NOT_EXISTS_PATH) {
            System.out.println(prevVertex + "-" + prev[prevVertex]);
            prevVertex = prev[prevVertex];
        }
    }

    //未访问过的顶点中的最小路径
    private static int findMin(int[] dist, boolean[] visit) {
        int minWeight = MAX_WEIGHT;
        int minVertex = NOT_EXISTS_PATH;
        for (int i = 0; i < dist.length; i++) {
            if (!visit[i] && dist[i] < minWeight) {
                minWeight = dist[i];
                minVertex = i;
            }
        }
        return minVertex;
    }

    private static ArrayList<Vertex>[] initDemo(int vertexNum) {
        ArrayList<Vertex>[] list = new ArrayList[vertexNum];
        String[] demo = new String[vertexNum];
        //顶点id, 顶点权重weight（距离）;
        demo[0] = "1,4;2,6;3,6";
        demo[1] = "4,9;2,1";
        demo[2] = "4,6;5,4";
        demo[3] = "2,2;5,1";
        demo[4] = "6,6";
        demo[5] = "4,1;6,8";
        demo[6] = "";

        for (int i = 0; i < vertexNum; i++) {
            ArrayList<Vertex> vertexList = new ArrayList<>();
            if (demo[i] == null || demo[i].length() == 0) {
                list[i] = vertexList;
                continue;
            }
            String[] its = demo[i].split(";");
            for (String kv : its) {
                String[] kvIts = kv.split(",");
                vertexList.add(new Vertex(Integer.parseInt(kvIts[0]), Integer.parseInt(kvIts[1])));
            }
            list[i] = vertexList;
        }
        return list;
    }

    private static void print(ArrayList<Vertex>[] list) {
        //打印顶点
        int index = 0;
        for (ArrayList<Vertex> arrayList : list) {
            System.out.println(index + " " + arrayList);
            index++;
        }
    }

    private static class Vertex {
        int id;
        int weight;

        public Vertex(int id, int weight) {
            this.id = id;
            this.weight = weight;
        }

        @Override
        public String toString() {
            return "Vertex{" +
                    "id=" + id +
                    ", weight=" + weight +
                    '}';
        }
    }
}

输出

0 [Vertex{id=1, weight=4}, Vertex{id=2, weight=6}, Vertex{id=3, weight=6}]  #演示数据对应的各顶点信息，id为顶点名称0-6，weight为路径长度
1 [Vertex{id=4, weight=9}, Vertex{id=2, weight=1}]
2 [Vertex{id=4, weight=6}, Vertex{id=5, weight=4}]
3 [Vertex{id=2, weight=2}, Vertex{id=5, weight=1}]
4 [Vertex{id=6, weight=6}]
5 [Vertex{id=4, weight=1}, Vertex{id=6, weight=8}]
6 []
minVertex 0 dist [0, 4, 6, 6, 999, 999, 999] visit [true, false, false, false, false, false, false] prev [-1, 0, 0, 0, -1, -1, -1] #minVertex是当前的最小路径的顶点0，dist为当前各顶点的路径和，visit为标记顶点是否访问 prev记录顶点的前一个顶点，用于记录最终的最短路径
minVertex 1 dist [0, 4, 5, 6, 13, 999, 999] visit [true, true, false, false, false, false, false] prev [-1, 0, 1, 0, 1, -1, -1]
minVertex 2 dist [0, 4, 5, 6, 11, 9, 999] visit [true, true, true, false, false, false, false] prev [-1, 0, 1, 0, 2, 2, -1]
minVertex 3 dist [0, 4, 5, 6, 11, 7, 999] visit [true, true, true, true, false, false, false] prev [-1, 0, 1, 0, 2, 3, -1]
minVertex 5 dist [0, 4, 5, 6, 8, 7, 15] visit [true, true, true, true, false, true, false] prev [-1, 0, 1, 0, 5, 3, 5]
minVertex 4 dist [0, 4, 5, 6, 8, 7, 14] visit [true, true, true, true, true, true, false] prev [-1, 0, 1, 0, 5, 3, 4]
6-4  #最终最短路径对应的各个边
4-5
5-3
3-0

流程图

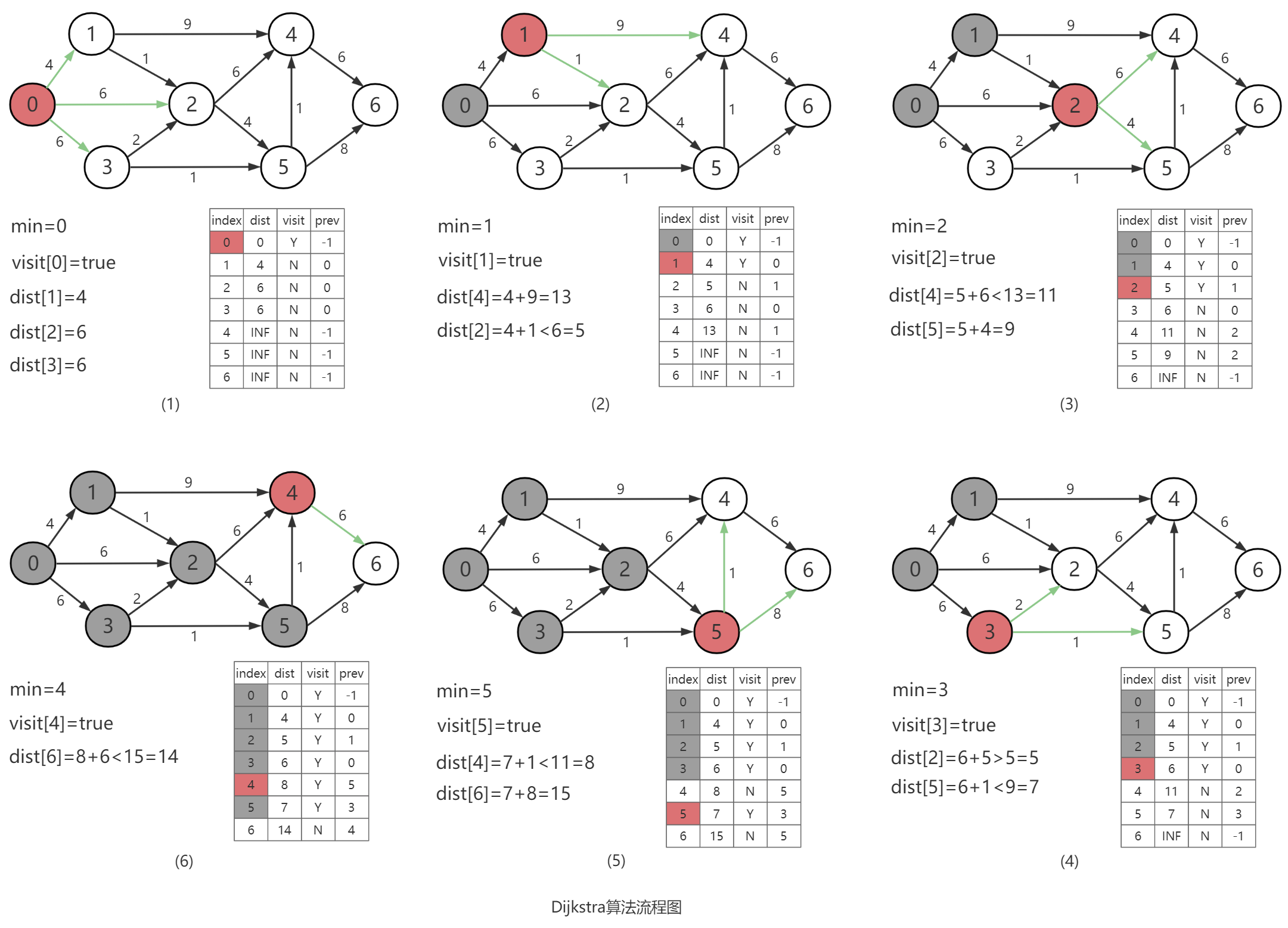
可以看出算法核心是这三个数组：

一是顶点的状态数组visit，顶点一旦标记为访问过（true），后续就无需再处理这些顶点；

二是各顶点当前路径之和的dist数组，每次需要从中选出一条未访问过的顶点的最小路径和的顶点，再根据它取出对应的各边来处理；

三是存储各顶点前一个顶点的数组prev，用于还原出最短路径对应的各个边。

另外顶点数据存储用的是邻接表，数组下标为顶点id，值是一个ArrayList，里面存储了对应的顶点和权值。

 

参考资料
https://handwiki.org/wiki/:Dijkstra's%20algorithm
https://www.programiz.com/dsa/dijkstra-algorithm