线性排序

 我们都考一百分，就都是第一名了——用分组的方法来避免排序

之前介绍的几种排序算法都涉及到各元素间的比较、移动，能否避免或者尽量减少这些开销呢？接下来要介绍的几种“线性排序”方法或许能带给我们新思路。

一 桶排序

对数据进行分桶（分组），再按桶的顺序来处理数据。也有之前提到的“分治”的意思。有些特殊数据，例如0-100岁的人群、考试分数，都是范围相对固定，且远小于元素的数量。可以针对这个特性来设计特定的排序算法。

看个具体例子：如何按照学分来排序，代码如下

import java.util.Arrays;

public class BucketSort {
    public static void main(String[] args) {
        //10个学生 按学分排序 学分范围为0-5
        int[] numbers = {3, 2, 5, 1, 3, 5, 2, 0, 1, 2};
        System.out.println(Arrays.toString(numbers));
        //0-5学分对应6个桶（组）
        int bucketNum = 6;
        int[] buckets = new int[bucketNum];
        //统计每个桶里所属的学分的出现次数
        for (int number : numbers) {
            buckets[number] += 1;
        }
        System.out.println(Arrays.toString(buckets));
        //按照桶的大小顺序来显示数据
        int index = 0;
        for (int i = 0; i < bucketNum; i++) {
            for (int j = 0; j < buckets[i]; j++) {
                numbers[index] = i;
                index++;
            }
        }
        System.out.println(Arrays.toString(numbers));
    }
}

 输出说明

[3, 2, 5, 1, 3, 5, 2, 0, 1, 2]
[1, 2, 3, 2, 0, 2] #按桶的顺序统计每个学分的出现次数，这里情况比较特殊，学分的位置就是桶的编号
[0, 1, 1, 2, 2, 2, 3, 3, 5, 5] #按桶的编号从小到大打印出来就排序好了

各个学分的统计人数如图示：

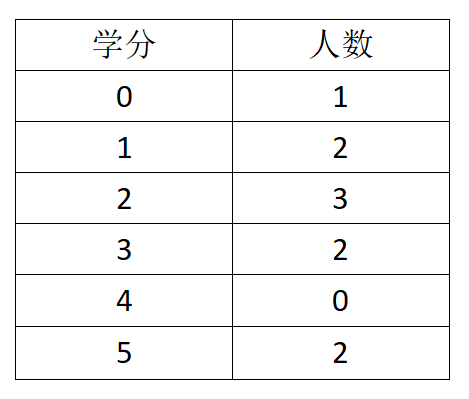
可以看到代码第20行“numbers[index] = i”直接把桶编号当作了元素，其实是忽略掉了原始数组中数出现的顺序，导致了“非原地”排序。例如[2 2 1]，排序后为[1 2 2]，其中第一个2有可能不是[2 2 1]中的第一个2，单独看这个2是否原地没影响，但实际开发中，可能是两个不同的对象的某个属性都是2。

例如两个用户对象{"uid":3,"type":2} {"uid":4,"type":2}，我们按照type属性排序时不希望后出现的对象{"uid":4,"type":2}排到前面。如果需要原地排序，可以按元素出现顺序依次保存到对应桶里，之后再按照写入顺序读取即可。

二 计数排序

可以看作是桶排序的一种扩展，在统计每个元素出现次数的同时，计算出截至到某个桶时累计的元素个数，用于还原出每个元素的具体位置。

代码如下

import java.util.Arrays;

public class CountingSort {
    public static void main(String[] args) {
        int[] numbers = {3, 5, 4, 1, 3, 0, 1};
        System.out.println(Arrays.toString(numbers));
        //找到最大值
        int max = numbers[0];
        for (int number : numbers) {
            if (number > max) {
                max = number;
            }
        }
        System.out.println("max " + max);

        int[] numbersCount = new int[max + 1];
        for (int number : numbers) {
            numbersCount[number] = numbersCount[number] + 1;
        }
        System.out.println("number count " + Arrays.toString(numbersCount));
        //个数累计
        int numberCount = 0;
        for (int i = 0; i < numbersCount.length; i++) {
            numberCount += numbersCount[i];
            numbersCount[i] = numberCount;
        }
        System.out.println("number sum   " + Arrays.toString(numbersCount));

        int[] sortedNumbers = new int[numbers.length];
        //从数组右侧开始处理
        for (int i = numbers.length - 1; i > -1; i--) {
            System.out.print("pos " + i + " value " + numbers[i] + " numberCount" + numbersCount[numbers[i]]);
            int pos = numbersCount[numbers[i]] - 1;
            numbersCount[numbers[i]] = pos;
            sortedNumbers[pos] = numbers[i];
            System.out.println("->" + pos + Arrays.toString(sortedNumbers));
        }
        System.out.println(Arrays.toString(sortedNumbers));
    }
}

输出说明

[3, 5, 4, 1, 3, 0, 1]
max 5 #找到最大值
number count [1, 2, 0, 2, 1, 1] #每个分数的出现次数
number sum   [1, 3, 3, 5, 6, 7] #截至到每个桶时的分数出现次数累计
pos 6 value 1 numberCount3->2[0, 0, 1, 0, 0, 0, 0] #从右侧向左处理各个元素 取出最右侧的1，对应桶1，对应累计出现次数为3，所以元素1排序后的位置是3-1=2，【同时需要把次数-1后的值更新到桶累计次数中】
pos 5 value 0 numberCount1->0[0, 0, 1, 0, 0, 0, 0] #取元素0，对应桶0，次数为1，最终位置为1-1=0
pos 4 value 3 numberCount5->4[0, 0, 1, 0, 3, 0, 0] #取元素3，对应桶3，次数为5，最终位置为5-1=4
pos 3 value 1 numberCount2->1[0, 1, 1, 0, 3, 0, 0] #取元素1，对应桶2，次数为2，最终位置为2-1=1
pos 2 value 4 numberCount6->5[0, 1, 1, 0, 3, 4, 0] #取元素4，对应桶4，次数为6，最终位置为6-1=5
pos 1 value 5 numberCount7->6[0, 1, 1, 0, 3, 4, 5] #取元素5，对应桶5，次数为7，最终位置为7-1=6
pos 0 value 3 numberCount4->3[0, 1, 1, 3, 3, 4, 5] #取元素3，对应桶3，次数为4，最终位置为4-1=3
[0, 1, 1, 3, 3, 4, 5]

 各学分数量和累计如图：

 

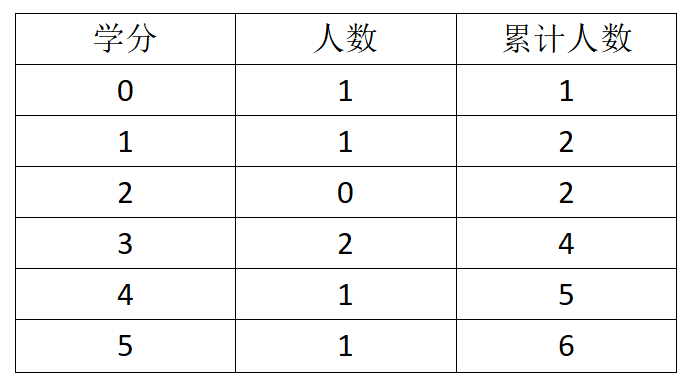
排序过程如图：

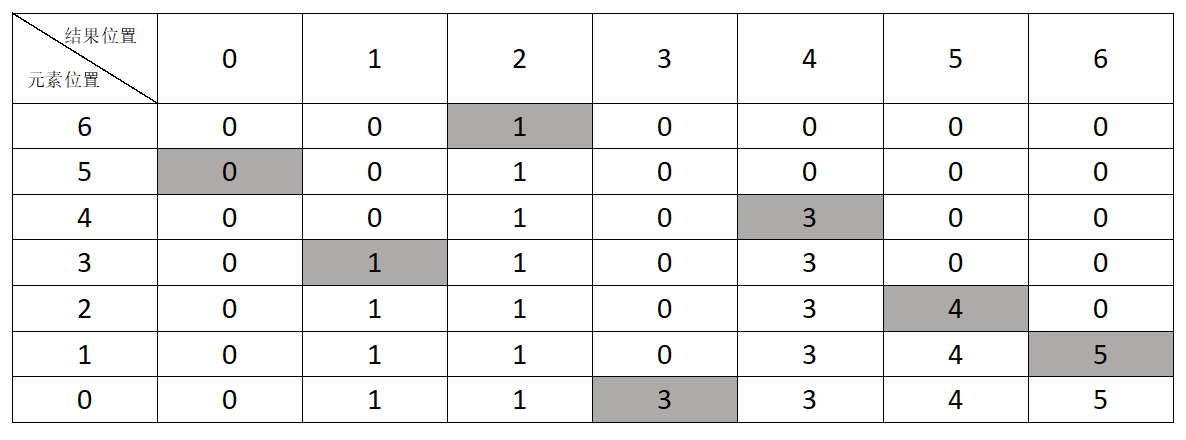
三 基数排序

所谓基数排序，就是把数分成了多个分位，按照每个分位来分桶排序，例如123，分为百分位的1，十分位的2，个分位的3。

演示代码如下，注意我们用Map模拟了各个桶对应的存储文件，实际使用时可以用每个桶对应一个文件。

import java.util.*;

public class RadixSort {
    public static void main(String[] args) {
        String[] numbers = {"354", "130", "152", "251", "401", "210"};
        System.out.println(Arrays.toString(numbers));
        //假定数据都是3位长度（不够可以左侧补0）
        int numberLength = 3;
        //0-9对应10个桶
        int bucketNum = 10;
        int[] buckets = new int[bucketNum];

        //用Map模拟桶对应的10个文件，key是桶名称，value是该桶里的元素
        Map<Integer, List<String>> numbersMap = new HashMap<>();

        //从右往左取，每次取一位 例如456，第一次取6，第二次取5，第三次取4
        for (int i = numberLength; i > 0; i--) {
            System.out.print("pos " + i + "\n\t");
            for (String num : numbers) {
                int tmp = Integer.parseInt(num.substring(i - 1, i));
                System.out.print(tmp + " ");
                //该位出现的次数
                buckets[tmp] += 1;
                //初始化桶对应的元素列表
                numbersMap.putIfAbsent(tmp, new ArrayList<>());
                //追加对应的元素
                numbersMap.get(tmp).add(num);
            }
            System.out.println("\n\t" + Arrays.toString(buckets));
            int numIndex = 0;
            for (int j = 0; j < bucketNum; j++) {
                //跳过无数据的桶
                if (buckets[j] == 0) {
                    continue;
                }
                //读取桶里的元素
                for (String e : numbersMap.get(j)) {
                    //元素按“当前位”排序后的位置
                    numbers[numIndex] = e;
                    numIndex++;
                }
                //重置桶数量
                buckets[j] = 0;
            }
            System.out.println("\t" + Arrays.toString(numbers));
            numbersMap.clear();
        }
    }
}

输出说明

[354, 130, 152, 251, 401, 210]
pos 3 #从右侧往左处理
	4 0 2 1 1 0 #各元素最右侧的位值
	[2, 2, 1, 0, 1, 0, 0, 0, 0, 0] #该位出现的次数统计
	[130, 210, 251, 401, 152, 354] #按从小到大的桶编号来直接取出桶的元素，就是按当前位排序后的元素，更新原有数组
pos 2 #元素右侧第二个
	3 1 5 0 5 5 #各元素的位值
	[1, 1, 0, 1, 0, 3, 0, 0, 0, 0] #次数统计
	[401, 210, 130, 251, 152, 354] #按桶排序，并更新原有数组
pos 1 #右侧第三个
	4 2 1 2 1 3 #各元素的位值 
	[0, 2, 2, 1, 1, 0, 0, 0, 0, 0] #次数统计
	[130, 152, 210, 251, 354, 401] #按桶排序，并更新原有数组

总结

三种排序方法都是对数据的分桶，按照桶自身的顺序来处理各个元素，不涉及元素间的比较，时间复杂度是“线性”的（参与排序的元素数量和算法的时间复杂度的关系是一次方函数关系，如x=2y、x=2y+1），所以统称为“线性排序”。

另外，使用时一定要根据数据特点，评估桶的数量是否可控，选择适合的算法。

 

扩展思考

1 桶数量和元素数量一样时会出现什么情况？

2 计数排序时为何从右侧开始处理元素？

3 基数排序时如果遇到小数应该怎么处理？