对归并排序和快速排序的理解

处理好这段数据就行——分治的思想来解决排序问题

有了之前的预备知识，我们正式开始归并排序和快速排序。

一 归并排序

核心思想是“分治”，把整体拆解成部分，对部分进行排序后再合并。涉及到二分法、递归、有序数组合并三个方法。

首先说二分法，就是对一个数组不断的从中间切分，每切分一次就分成左右两部分，然后再对左右两部分再切分，直到每部分都只剩一个元素。比如[2 5 1 3 4]不断的从中间分割，最终分成独立的 [2] [5] [1] [3] [4] 如图：

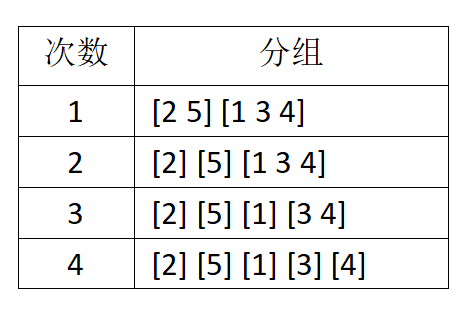
其次是递归，可以理解为函数调用自己，但是每次调用传递的参数是不同的，同时存在可退出的条件。

最后是“有序数合并”，就是把两个有序数组合并为一个有序数组，我们上次已经详细介绍过（见问题一）。

我们把三个步骤结合起来：

1 把数组切分成左右两部分

2 分别对左右两部分数组递归调用步骤1，直到元素数量为1

3 合并左右排序好的数据

具体代码如下

import java.util.Arrays;

public class MergeSort {
    public static void main(String[] args) throws InterruptedException {
        int[] numbers = {2, 5, 1, 6, 4, 3, 7};
        System.out.println("*sorted" + Arrays.toString(sort(numbers, "left ")));
    }

    //direction仅用于打印数组左右部分，和排序无关
    private static int[] sort(int[] numbers, String direction) {
        //从中间切分
        int splitIndex = numbers.length / 2;
        System.out.println(direction + " start " + Arrays.toString(numbers) + " splitIndex " + splitIndex);
        //只剩一个时无需再处理
        if (numbers.length == 1) {
            return numbers;
        }
        //按照中间位置切分成两个数组
        int[] left = splitArray(numbers, 0, splitIndex);
        int[] right = splitArray(numbers, splitIndex, numbers.length);

        //递归处理两侧数据
        int[] a = sort(left, "left ");
        int[] b = sort(right, "right");
        //合并两侧数据
        int[] merge = mergeSortedArray(a, b);
        System.out.println(direction + " end  " + " a" + Arrays.toString(a) + "+b" + Arrays.toString(b) + "=" + Arrays.toString(merge));
        return merge;
    }

    private static int[] splitArray(int[] arr, int start, int end) {
        int length = end - start;
        int[] tmp = new int[length];
        System.arraycopy(arr, start, tmp, 0, length);
        return tmp;
    }

    private static int[] mergeSortedArray(int[] a, int[] b) {
        //初始化一个新的数组，长度为ab数组之和
        int[] merge = new int[a.length + b.length];
        //merge的写入位置 用来记录写入到哪了
        int mergeIndex = 0;
        //a数组读取的位置 用来记录读取到哪了
        int aIndex = 0;
        //b数组读取的位置
        int bIndex = 0;
        //从a数组开始处理（当然从b数组开始也可以）和b数组的值依次比较，谁小就写入merge中，保证了写入的值就是从小到大的
        for (int i = aIndex; i < a.length; i++) {
            //a数组元素依次和b数组元素比较
            for (int j = bIndex; j < b.length; j++) {
                //a的元素比b中的小 merge里写a 否则写b
                if (a[i] < b[j]) {
                    merge[mergeIndex] = a[i];
                    //写完后，mergeIndex和aIndex都要移动到下一个
                    mergeIndex++;
                    aIndex++;
                    //由于b中元素是从小到大排列的 只要发现比b中元素小 后续的b元素就无需再比较了，节省了后续的比较开销（特性1）
                    break;
                } else {
                    //小的落在了b数组，那就写它
                    merge[mergeIndex] = b[j];
                    //同样写完对应的mergeIndex和bIndex都要移动到下一个
                    mergeIndex++;
                    bIndex++;
                }
            }
        }
        //由于a数组中可能存在元素都大于b数组的值，导致a数组后续值未处理（b数组同理），因此检查a数组或b数组是否都处理完，有剩余直接写入到merge中即可。
        for (; aIndex < a.length; aIndex++) {
            merge[mergeIndex] = a[aIndex];
            mergeIndex++;
        }
        for (; bIndex < b.length; bIndex++) {
            merge[mergeIndex] = b[bIndex];
            mergeIndex++;
        }
        return merge;
    }
}

 输出说明

left  start [2, 5, 1, 6, 4, 3, 7] splitIndex 3 #数组长度除2当中切分位置，切分后左侧为[2 5 1] 右侧为[6 4 3 7]
left  start [2, 5, 1] splitIndex 1 #从左侧继续切分，继续分为左右两侧
left  start [2] splitIndex 0 #继续左侧2，剩余一个元素退出
right start [5, 1] splitIndex 1 #处理上一步中的右侧数据 5 1，继续切分为左右
left  start [5] splitIndex 0 #左侧的5，剩余一个元素退出
right start [1] splitIndex 0 #右侧的1，剩余一个元素退出
right end   a[5]+b[1]=[1, 5] #右侧的1处理完毕后，这时左侧数据为最后一次返回的数据5，这时把5 1交给mergeSortedArray方法处理，结果为[1 5]
left  end   a[2]+b[1, 5]=[1, 2, 5] #返回的合并结果再和它上一层的左侧递归结果2调用mergeSortedArray，结果为[1 2 5]，此时第一层的左侧结果已经处理完毕
right start [6, 4, 3, 7] splitIndex 2 #开始第一层的右侧部分
left  start [6, 4] splitIndex 1 #再次开始切分左右
left  start [6] splitIndex 0 #剩余一个元素退出
right start [4] splitIndex 0 #剩余一个元素退出
left  end   a[6]+b[4]=[4, 6] #合并
right start [3, 7] splitIndex 1 #切分
left  start [3] splitIndex 0 #切分，退出
right start [7] splitIndex 0 #切分，退出
right end   a[3]+b[7]=[3, 7] #合并
right end   a[4, 6]+b[3, 7]=[3, 4, 6, 7] #合并
left  end   a[1, 2, 5]+b[3, 4, 6, 7]=[1, 2, 3, 4, 5, 6, 7] #达到第一层的左右数据合并，完成最终数据的合并，处理流程结束。
*sorted[1, 2, 3, 4, 5, 6, 7] 

二 快速排序

核心是按某个元素分割数据，使左侧数据小于它，右侧数据大于它。主要分以下几个步骤

1 选取某个元素当作基准值（一般选最右侧数据）

2 把小于基准值的数据移动到它的左侧，大于它的移动到右侧

3 按步骤1、2分别递归处理基准值左侧和右侧数据

代码如下

import java.util.Arrays;

public class QuickSort {
    public static void main(String[] args) {
        int[] numbers = {1, 3, 5, 2, 6, 4};
        System.out.println(Arrays.toString(numbers));
        quickSort(numbers, 0, numbers.length - 1, "left ");
        System.out.println("*sorted" + Arrays.toString(numbers));
    }

    //direction仅用于打印数组左右部分，和排序无关
    private static void quickSort(int[] numbers, int leftIndex, int rightIndex, String direction) {
        if (rightIndex - leftIndex <= 0) {
            return;
        }
        int pivotPos = partition(numbers, leftIndex, rightIndex);
        System.out.print(direction + " pivot " + numbers[pivotPos] + " pivotPos " + pivotPos);
        System.out.println(" leftIndex " + leftIndex + " rightIndex " + rightIndex + Arrays.toString(numbers));
        quickSort(numbers, leftIndex, pivotPos - 1, "left ");
        quickSort(numbers, pivotPos + 1, rightIndex, "right");
    }

    private static int partition(int[] numbers, int leftIndex, int rightIndex) {
        //默认把数组最右侧一个当成轴
        int pivotPos = rightIndex;
        int pivotNum = numbers[pivotPos];
        //从轴向左一位开始
        rightIndex -= 1;

        while (true) {
            //左侧元素处理
            while (numbers[leftIndex] < pivotNum) {
                //只要比轴小 就一直向右移动索引
                leftIndex++;
            }
            //右侧元素处理
            while (numbers[rightIndex] > pivotNum) {
                //只要比轴大 就向左侧移动索引
                rightIndex--;
                if (rightIndex < 0) {
                    break;
                }
            }
            if (leftIndex >= rightIndex) {
                break;
            } else {
                //交换元素
                int tmp = numbers[rightIndex];
                numbers[rightIndex] = numbers[leftIndex];
                numbers[leftIndex] = tmp;
            }
        }
        //交换轴和左侧索引对应的值，此时数据真正分成了两部分，左侧是小于轴的，右侧是大于轴的
        numbers[pivotPos] = numbers[leftIndex];
        numbers[leftIndex] = pivotNum;
        return leftIndex;
    }
}

 输出说明

[1, 3, 5, 2, 6, 4]
left  pivot 4 pivotPos 3 leftIndex 0 rightIndex 5[1, 3, 2, 4, 6, 5] #第一次为确定基准值，选取最右侧的4为基准值，处理完毕左侧为1 3 2 右侧为 6 5
left  pivot 2 pivotPos 1 leftIndex 0 rightIndex 2[1, 2, 3, 4, 6, 5] #第二次选取4左侧的区间段数据[1 3 2]开始处理，选取此区间段的最右侧2为基准值来处理
right pivot 5 pivotPos 4 leftIndex 4 rightIndex 5[1, 2, 3, 4, 5, 6] #第三次选择4右侧的区间段数据[6 5]开始处理，选取此区间的最右侧5为基准值来处理
*sorted[1, 2, 3, 4, 5, 6]

总结

我们看到两种算法都对数据进行了分段处理，都是递归调用。不同的是归并排序分割完毕后是从下向上排序，最终再合并结果。而快速排序是从最上层就开始处理（基准值处理完它的位置就已经固定了），一直到所有分区处理完毕。

另外，需要注意对内存的占用，归并排序由于要合并左右分区数据，必须要申请一个大小为左右数量之和的内存来保存合并结果。还有由于两者都是递归调用，涉及栈的不断压入，必须考虑栈的调用深度。

归并算法是不断从中间切分数据，所以栈的深度最大为log₂N(即以2为底的N的对数，N为数组的个数，也就是对N一直除2)。看下不同数量级的对数，大概有个体感：

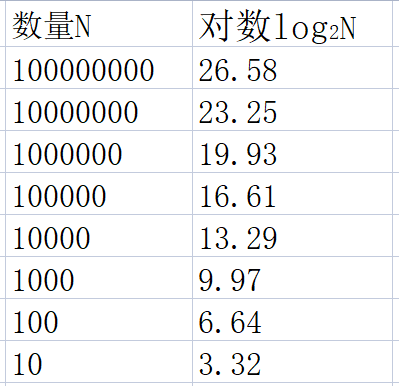
可以看到一百万数量的数组，分割19次左右就能达到1。而快速排序中如果给定数据本身就是一个从小到大的数，导致每次分区后基准数总位于分区的最右侧，那么栈的最大深度就等于数据量，这时很容易导致栈溢出。

 

扩展思考

如何减少快速排序中的递归深度？

快速排序中基准值位置确定这个特性有没有其他用途？