【题解】CF1789C Serval and Toxel's Arrays
题面传送门
解决思路
因为每个数列内的数字不重复,所以我们考虑每个数在多少个数列中出现过。记数字
已知一共有
- 取出一个含
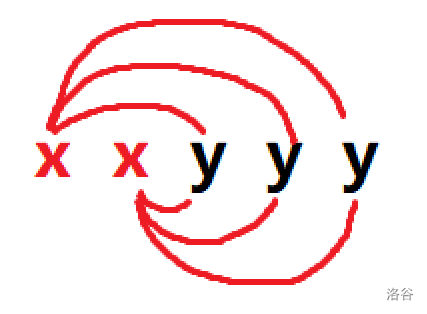
- 取出两个含
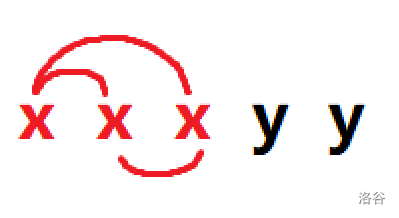
这样答案就很明了了。
然后考虑如何求出每个数出现的次数。
记
AC Code
//If, one day, I finally manage to make my dreams a reality...
//I wonder, will you still be there by my side?
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
#define TIE cin.tie(0),cout.tie(0)
#define int long long
#define y1 cyy
#define fi first
#define se second
#define cnt1(x) __builtin_popcount(x)
#define mk make_pair
#define pb push_back
#define pii pair<int,int>
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define lbt(x) (x&(-x))
using namespace std;
int T,n,m,a[200005],cnt[400005],lst[400005],x,y;
string s;
void solve(){
cin>>n>>m;
for(int i=1;i<=n+m;i++) cnt[i]=0,lst[i]=-1;
for(int i=1;i<=n;i++) cin>>a[i],lst[a[i]]=0;
for(int i=1;i<=m;i++){
cin>>x>>y;
if(a[x]!=y){
cnt[a[x]]+=i-lst[a[x]],lst[a[x]]=-1;
lst[y]=i,a[x]=y;
}
}
for(int i=1;i<=n+m;i++) if(lst[i]!=-1) cnt[i]+=m-lst[i]+1;
int ans=0;
for(int i=1;i<=n+m;i++){
ans+=cnt[i]*(m+1-cnt[i]);
ans+=cnt[i]*(cnt[i]-1)/2;
}
cout<<ans<<endl;
}
signed main(){
IOS;TIE;
cin>>T;
while(T--) solve();
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 25岁的心里话