【题解】 CF1737C Ela and Crickets

题面传送门

题目翻译

给定一个 $n\times n$ 的棋盘，棋盘上有且仅有三颗排成 $\text{L}$ 形的棋子。

对于 $\text{L}$ 形的定义，有且仅有以下四种情况：

，，，

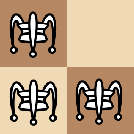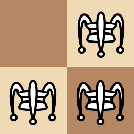棋子的移动规则和跳棋相同。它可以水平、垂直或斜向移动。当且仅当一个棋子的某个方向紧随另一个棋子时，它能跳到另一个棋子之后的一个方格上。棋子不能跳出棋盘。详见样例解释。

现在有 $T$ 组询问，每组给出棋盘大小 $n(n\le {10}^5)$，三颗棋子各自的位置 $r_1,c_1,r_2,c_2,r_3,c_3(1\le r_1,c_1,r_2,c_2,r_3,c_3\le n)$，以及目标点 $x,y(1\le x,y\le n)$，询问是否能使其中的一颗棋子跳到目标点。输出 YES 或 NO。

解决思路

当没有什么思路的时候可以先模拟一下棋子的跳跃过程。

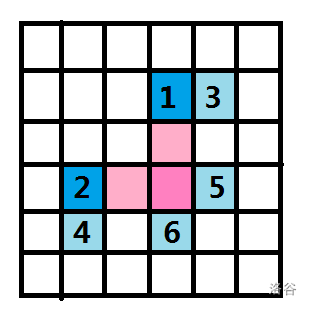
例如上图粉色的 $\text{L}$ 形，经过一次跳跃，其折点可以跳到 $1,2$ 处，非折点可以跳到 $3,4,5,6$。

我们进行分类讨论：

1. 跳折点（$1,2$）

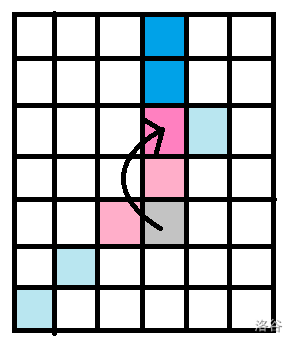
此后原先折点可以和另一点在一列上不断跳，原先两个非折点可以不断斜向跳，但图中如果左下的跳到右上则又变成了 $\text{L}$ 形，原先折点还是折点。

同时发现，可以跳到的任意点，其横纵坐标，一定有一个和原先折点奇偶性相同。就算重新变 $\text{L}$ 形，新折点的横纵坐标一定有一个和原先折点奇偶性相同，所以结论仍成立。

2. 斜跳非折点（$3,4$）

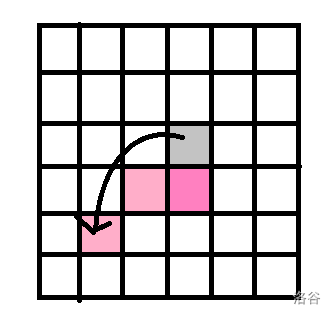
发现就是情况 $1$ 镜像翻转了一下。

3. 直跳非折点（$5,6$）

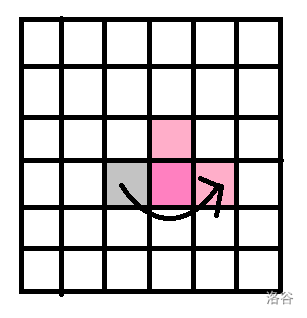
发现又变成了 $\text{L}$ 形（情况 $1$ 已讲）。

由此，可以得出，若目标横纵坐标有一个和原先折点奇偶性相同，则可以到达。

然而发现样例都过不了。

考虑后可以发现有特殊情况：

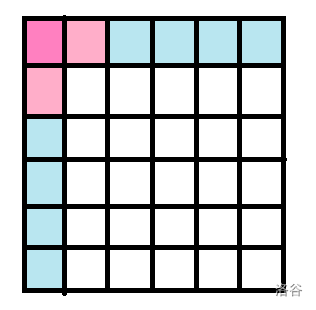
当原先折点在棋盘角落时，只能到达两条边上的点（因为跳不出去）。

所以特判一下就好。

至于如何判断那个是折点，输入每一个 $x,y$ 后排序，$x_2,y_2$ 就是 。

AC Code

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
#define TIE cin.tie(0),cout.tie(0)
#define int long long
using namespace std;
int T,n,x[4],y[4],tx,ty;
bool check(){
	bool _1=0,_2=0;
	if((x[2]==1||x[2]==n)&&tx!=x[2]) _1=1;
	if((y[2]==1||y[2]==n)&&ty!=y[2]) _2=1;
	if(_1&&_2) return 0;
	if(((x[2]+tx)&1)&&((y[2]+ty)&1)) return 0;
	return 1;
}
void solve(){
	cin>>n;
	for(int i=1;i<=3;i++) cin>>x[i]>>y[i];
	cin>>tx>>ty;
	sort(x+1,x+4),sort(y+1,y+4);
	if(check()) cout<<"YES"<<endl;
	else cout<<"NO"<<endl; 
} 
signed main(){
	IOS;TIE;
	cin>>T;
	while(T--) solve();
	return 0;
}