【题解】 CF993A Two Squares

题面传送门

解决思路

考虑到点的坐标范围很小，所以可以直接用二维数组，把第一个正方形所在的位置打上标记，然后扫第二个正方形所在的范围，如果有标记就输出 \(\text{YES}\)，都没有就输出 \(\text{NO}\) 。

思路很简单，但是实现的细节有些麻烦：

• 坐标可能有负数，所以全部 \(+100\)

• 给出坐标的顺序不确定，所以要排序

• 在平面直角坐标系中，行为 \(y\)，列为 \(x\)，同时 \(y\) 值是上大下小的。写循环时要保持头脑清醒 \(\text{qwq}\)

• 正方形的顶点与边相交也算相交，所以无需对第二个正方形的顶点坐标做 \(+1\ \text{or} -1\) 的处理

以样例 \(1\) 为例：

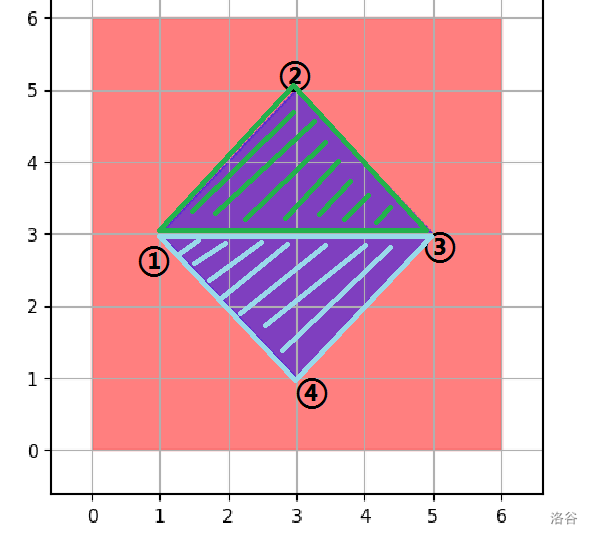
设排序后四个点的顺序如上图，可以分成上下两部分来算方便一些。具体遍历方法如下：

...

bool cmp(node a,node b){
	if(a.x==b.x) return a.y>b.y;
	return a.x<b.x;
}
signed main(){
	IOS;TIE;
    
	...
    
	sort(a+1,a+5,cmp);
	swap(a[3],a[4]);      //得到顺序
    
	for(int i=a[4].y;i<=a[1].y;i++){     //遍历上半部分
		len=i-a[4].y;
		for(int j=a[4].x-len;j<=a[4].x+len;j++){
			if(vis[i][j]){
				cout<<"YES"<<endl;
				return 0;
			}
		}
	}
    
	for(int i=a[1].y;i<=a[2].y;i++){     //遍历下半部分
		len=a[2].y-i;
		for(int j=a[2].x-len;j<=a[2].x+len;j++){
			if(vis[i][j]){
				cout<<"YES"<<endl;
				return 0;
			}
		}
	}
    
	cout<<"NO"<<endl;
	return 0;
}

剩余部分代码很简单，就不给出了。