【题解】 CF446A DZY Loves Sequences

题面传送门

解决思路

本题可以从最多更改一个数字突破。修改后期望的最长严格递增子段应该是从这个数向两侧拓展的。

考虑什么时候可以构成严格递增子段。

设修改的数为 \(a_x\)，其严格递增子段长度为：

\(\begin{cases}a_{x+1}-a_{x-1}\ge 2 & f1_{x-1}+f2_{x+1} +1\\a_{x+1}-a_{x-1}< 2 & \max(f1_{x-1},f2_{x+1} )+1\end{cases}\)

其中 \(f1_i\) 为以 \(i\) 结尾的最长严格递增子段长度， \(f2_i\) 为以 \(i\) 开头的最长严格递增子段长度。

以 \(a_{x+1}-a_{x-1}\) 与 \(2\) 的大小关系分类的依据是：中间要有一个数（也就是改动的那个数）。

形象理解就是，我们找到了两段距离为 \(1\) 的严格递增子段，但它们之间的一个数凸出来或凹下去了，我们可以通过拉平这样一个数得到一个更长的严格递增子段。

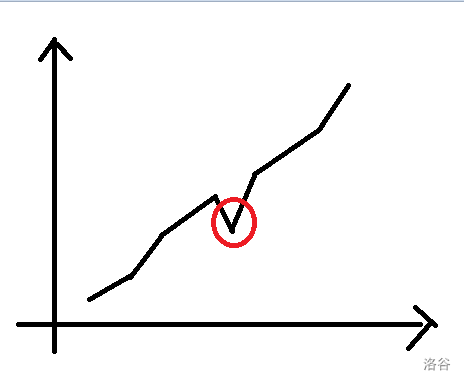
然后代码实现就很简单了。

AC Code

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
#define TIE cin.tie(0),cout.tie(0)
#define int long long
using namespace std;
int n,a[100005],f1[100005],f2[100005],ans;
signed main(){
	IOS;TIE;
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=n;i++) f1[i]=(a[i]>a[i-1])?f1[i-1]+1:1;
	for(int i=n;i>=1;i--) f2[i]=(a[i]<a[i+1])?f2[i+1]+1:1;
	for(int i=1;i<=n;i++){
		if(a[i+1]-a[i-1]>=2) ans=max(ans,f1[i-1]+f2[i+1]+1);
		else ans=max(ans,max(f1[i-1],f2[i+1])+1);
	}
	cout<<ans;
	return 0;
}