【笔记】CF1607F Robot on the Board 2 及相关

题目传送门

记忆化搜索

首先，这题 $10000$ 组 $2000\times 2000$ 的数据直接爆搜肯定会超时。想到，如果一个点的答案已经被更新过，之后走到这个点能再多走的点也就确定了，所以考虑记忆化搜索。然后就是分类讨论几种情况了（引用 HDWR 的图片）：

• 走出地图边界：

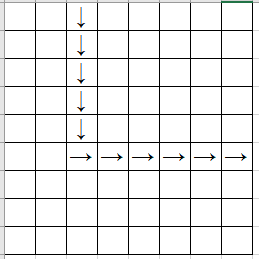
这时候只要从边界开始往回标号即可。所以搜索的时候需要把途经的点都按顺序记录下来。

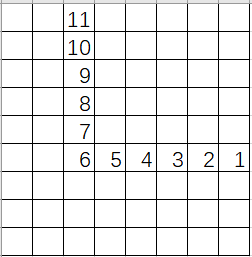
• 走到已经走过并记下答案路径上：

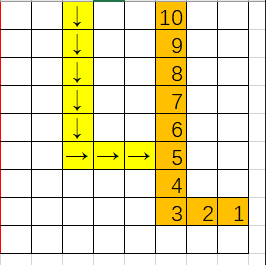
这种情况和走到边界很像，只要从碰到的那个点开始往回标号即可。

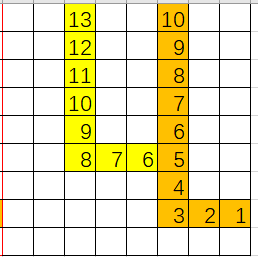
• 走到了本次搜索到的路径上，也就是出现了环：

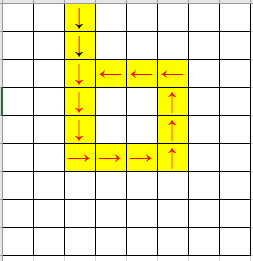
这时，环上的每一个点都可以走遍环上路径，所以标记答案为环的长度。剩下的部分是走向环的，所以从与环接触的点开始，依次往回标号即可。

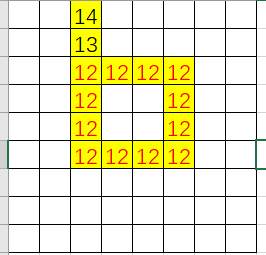
然后只要对每一个点 $dfs$ 一遍，找出最大的答案即可。

因为 $\sum n\times m\le 4\times {10}^6$，每个点只会被搜到一次，所以复杂度正确。

细节

首先，$\mathtt{\text{多}}\mathrm{组}\mathrm{数}\mathrm{据}!$

多测不清空， WA 两行泪。特别注意，是搜到边界外面时开始更新答案的，所以边界外面一圈也会有答案，清空的时候要大一圈！

其次，直接写深搜，这种做法会爆栈，MLE on #4 。

考虑到本题情况，不需要回溯，所以其实不用深搜，只要用 $while(1)$，每次在循环内改位置、编号即可。

Code

#include<bits/stdc++.h>
using namespace std;
int T,n,m,a[2005][2005],ans[2005][2005];
int cnth,ansn,ansx,ansy;
bool vis[2005][2005];
char c;
struct node{
	int x,y;
}q[4000005];
int turn(char c){
	if(c=='L') return 1;
	if(c=='R') return 2;
	if(c=='U') return 3;
	if(c=='D') return 4;
}
void init(){     //初始化
	for(int i=0;i<=n+1;i++){
		for(int j=0;j<=m+1;j++) ans[i][j]=vis[i][j]=0;
	}
	ansn=0;
}
void dfs(int x,int y,int k){
	while(1){
		if(x<1||y<1||x>n||y>m||ans[x][y]){ //走出边界或已经走到过
			for(int i=1;i<k;i++) ans[q[i].x][q[i].y]=ans[x][y]+k-i;
			return ;
		}
		if(vis[x][y]){  //出现环
			cnth=0;
			for(int i=1;i<k;i++){   //算不在环上的大小
				if(x==q[i].x&&y==q[i].y) cnth=i;
			}
			for(int i=1;i<cnth;i++) ans[q[i].x][q[i].y]=k-i;  //更新不在环上的答案
			for(int i=cnth;i<k;i++) ans[q[i].x][q[i].y]=k-cnth;  //更新环上答案
			return ;
		}
		vis[x][y]=1,q[k].x=x,q[k].y=y,k++;  //记录下当前状态并走向下一个状态
		if(a[x][y]==1) y--;
		else if(a[x][y]==2) y++;
		else if(a[x][y]==3) x--;
		else if(a[x][y]==4) x++;
	}
}
void print(){
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(ans[i][j]>ansn){
				ansn=ans[i][j];
				ansx=i,ansy=j;
			}
		}
	}
	printf("%d %d %d\n",ansx,ansy,ansn);
}
void solve(){
	scanf("%d%d",&n,&m);
	scanf("%c",&c);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m+1;j++){
			scanf("%c",&c);
			a[i][j]=turn(c);
		}
	}
	init();
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++) dfs(i,j,1);
	}
	print();
}
int main(){
	scanf("%d",&T);
	while(T--) solve();
	return 0;
}