【笔记】拓扑排序(Ⅰ)
题单
拓扑排序:将一个有向无环图 \((\ Directed\ Acyclic\ Graph,DAG\ )\) 进行排序进而得到一个有序的线性序列。
简单食用方法:\(vector\) 存图,再用 \(queue\) 跑 \(BFS\)。每次从入度为 \(0\) 的点开始。
0X00 B3644 家谱树
B题库来的,所以显然是板。
入度为 \(0\) 的点可以直接输出,之后找点,一旦入度减到 \(0\) 了就输出,这样可以保证每个人的后辈都比那个人后列出。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,m,x,in[105];
vector<int> a[105];
queue<int> q;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&x);
while(x){
in[x]++,a[i].push_back(x);
scanf("%d",&x);
}
}
for(int i=1;i<=n;i++){
if(!in[i]) q.push(i),printf("%d ",i);
}
while(q.size()){
int k=q.front();
q.pop();
for(int i=0;i<a[k].size();i++){
int tmp=a[k][i];
in[tmp]--;
if(!in[tmp]){
q.push(tmp);
printf("%d ",tmp);
}
}
}
return 0;
}
0X01 P1807 最长路
因为要存下一个点和路径长度,所以用结构体。
开始时将所有入度为 \(0\) 的入队。
每次找点时更新到这个点的最大距离,将 原来最大距离 与 到通向它的点的最大距离 \(+\) 这段路的距离 取 \(\max\)。
ans[tmp.to]=max(ans[tmp.to],ans[k]+tmp.dis);
同时将其入度减一(懒惰删点),如果入度为 \(0\) 就入队。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,m,in[1505],ans[1505],x,y,w;
bool vis[1505];
struct node{
int to,dis;
}k;
vector<node> a[1505];
queue<int> q;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&x,&y,&w);
in[y]++;
k.to=y,k.dis=w;
a[x].push_back(k);
}
memset(ans,-0x3f,sizeof(ans));
ans[1]=0;
for(int i=1;i<=n;i++) if(!in[i]) q.push(i);
while(q.size()){
int k=q.front();
q.pop();
for(int i=0;i<a[k].size();i++){
node tmp=a[k][i];
vis[tmp.to]=1;
ans[tmp.to]=max(ans[tmp.to],ans[k]+tmp.dis);
in[tmp.to]--;
if(!in[tmp.to]) q.push(tmp.to);
}
}
if(!vis[n]) printf("-1");
else printf("%d",ans[n]);
return 0;
}
0X02 P4017 最大食物链计数
因为统计最大食物链,所以记录入度的同时出度也应该记录。最后答案是所有出度为 \(0\) 的点的答案之和。
同样,每次找到一个点就更新它的答案(加上 到达通向它的那个点的食物链数):
ans[tmp]=(ans[tmp]+ans[k])%mod;
Code:
#include<bits/stdc++.h>
#define mod 80112002
using namespace std;
int n,m,in[5005],out[5005],x,y,ans[5005],Ans;
vector<int> a[5005];
queue<int> q;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d",&x,&y);
out[x]++,in[y]++;
a[x].push_back(y);
}
for(int i=1;i<=n;i++){
if(!in[i]){
ans[i]=1;
q.push(i);
}
}
while(q.size()){
int k=q.front();
q.pop();
for(int i=0;i<a[k].size();i++){
int tmp=a[k][i];
ans[tmp]=(ans[tmp]+ans[k])%mod;
in[tmp]--;
if(!in[tmp]) q.push(tmp);
}
}
for(int i=1;i<=n;i++){
if(!out[i]) Ans+=ans[i],Ans%=mod;
}
printf("%d",Ans);
return 0;
}
0X03 P6145 [USACO20FEB]Timeline G
巧妙地将日期问题转化为图上问题。
第 \(a\) 次和第 \(b\) 次的日期差即为 \(a\) 到 \(b\) 的路径长度。同时,给出的第 \(i\) 不早于的日期 \(S_i\) 可以看成一个超级原点 \(0\) 到 \(i\) 的距离。第 \(i\) 次的最早日期即为超级原点到 \(i\) 的最长路(要满足所有要求)。
所有可以将初始答案设为 \(S_i\),之后每次搜到一个点取 \(\max\)。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,m,c,ans[100005],in[100005],x,y,w;
struct node{
int to,val;
}k;
vector<node> a[100005];
queue<int> q;
int main(){
scanf("%d%d%d",&n,&m,&c);
for(int i=1;i<=n;i++) scanf("%d",&ans[i]);
for(int i=1;i<=c;i++){
scanf("%d%d%d",&x,&y,&w);
in[y]++;
k.to=y,k.val=w;
a[x].push_back(k);
}
for(int i=1;i<=n;i++) if(!in[i]) q.push(i);
while(q.size()){
int tt=q.front();
q.pop();
for(int i=0;i<a[tt].size();i++){
node tmp=a[tt][i];
ans[tmp.to]=max(ans[tmp.to],ans[tt]+tmp.val);
in[tmp.to]--;
if(!in[tmp.to]) q.push(tmp.to);
}
}
for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
return 0;
}
0X04 P2419 [USACO08JAN]Cow Contest S
看其他人的全是 \(Floyd\),然鹅我是跟着拓扑排序的标签找的这里的。所以给出我用拓扑排序的做法,虽然不及 \(Floyd\) 好写,但复杂度差不多。
首先想到,设一个人已经明确的比他强的人数为 \(c_1\),比他弱的人数为 \(c_2\),若 \(c_1+c_2=n-1\),那么他的排名就是可以确定的。
那么如何算 \(c\) ?以 \(c_1\) 为例:
对于 \(a\) 强于 \(b\),就由 \(a\) 向 \(b\) 建有向边。记 \(m_1[i][j]=1\) 时表示明确 \(j\) 强于 \(i\),所以需要在跑拓扑时更新 \(m_1\) 。设当前父节点为 \(k\),并有边连向 \(tmp\)。首先赋 \(m_1[tmp][k]=1\)。其次,因为比 \(k\) 还强的就一定比 \(tmp\) 强,所以找到所有的 \(z\) 满足 \(m_1[k][z]=1\),并赋 \(m_1[tmp][z]=1\) 即可。
\(c_2\) 同理。只需要反向建边,记 \(m_2[i][j]=1\) 时表示明确 \(j\) 弱于 \(i\),再跑一遍拓扑即可。
最后统计时,\(c_1[i]+c_2[i]\) 即为\(m_1[i][j]\) 或 \(m_2[i][j]\) 为 \(1\) 的总数 \((1\le j\le n)\)。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,m,in1[105],in2[105],x,y,ans;
bool m1[105][105],m2[105][105];
vector<int> bet[105],wos[105];
queue<int> q1,q2;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d",&x,&y);
in1[y]++,in2[x]++;
bet[y].push_back(x),wos[x].push_back(y);
}
for(int i=1;i<=n;i++){
if(!in1[i]) q1.push(i);
if(!in2[i]) q2.push(i);
}
while(q1.size()){
int k=q1.front();
q1.pop();
for(int i=0;i<wos[k].size();i++){
int tmp=wos[k][i];
m1[tmp][k]=1;
for(int j=1;j<=n;j++) if(m1[k][j]) m1[tmp][j]=1;
in1[tmp]--;
if(!in1[tmp]) q1.push(tmp);
}
}
while(q2.size()){
int k=q2.front();
q2.pop();
for(int i=0;i<bet[k].size();i++){
int tmp=bet[k][i];
m2[tmp][k]=1;
for(int j=1;j<=n;j++) if(m2[k][j]) m2[tmp][j]=1;
in2[tmp]--;
if(!in2[tmp]) q2.push(tmp);
}
}
for(int i=1;i<=n;i++){
int cnt=0;
for(int j=1;j<=n;j++) if(m1[i][j]||m2[i][j]) cnt++;
if(cnt==n-1) ans++;
}
printf("%d",ans);
return 0;
}
0X05 UVA1423 Guess
是正号就建正向边,负号就建反向边。然后跑拓扑就可以通过每次 \(-1\) 求出前缀和数组。
最后前缀和数组两两作差即可求出一组符合条件的答案。
注意每次要清空图,同时为前缀和数组赋初值。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,in[15],T,sum[15];
char c;
vector<int> a[15];
queue<int> q;
void solve(){
for(int i=0;i<=10;i++) a[i].clear(),sum[i]=20;
scanf("%d",&n);
for(int i=0;i<n;i++){
for(int j=i+1;j<=n;j++){
cin>>c;
if(c=='+') a[j].push_back(i),in[i]++;
if(c=='-') a[i].push_back(j),in[j]++;
}
}
for(int i=0;i<=n;i++) if(!in[i]) q.push(i);
while(q.size()){
int k=q.front();q.pop();
for(int i=0;i<a[k].size();i++){
int tmp=a[k][i];
sum[tmp]=sum[k]-1;
in[tmp]--;
if(!in[tmp]) q.push(tmp);
}
}
for(int i=1;i<=n;i++) printf("%d ",sum[i]-sum[i-1]);
printf("\n");
}
int main(){
scanf("%d",&T);
while(T--) solve();
return 0;
}
0X06 CF919D Substring
\(DP\) 与拓扑结合。\(f[i][j]\) 表示到 \(i\) 位置 \(j\) 的最大次数。
将 \(a-z\) 转成数字 \(0-25\),方便存储。
考虑转移,对于二十六个字母(\(j\)):
- 若是当前节点,则 \(f[tmp][j]=max(f[tmp][j],f[k][j]+1)\)
- 否则 \(f[tmp][j]=max(f[tmp][j],f[k][j])\)
其中 \(tmp\) 为当前搜到的节点,\(k\) 为其父节点。
然后考虑如何判环。例如以下情况:
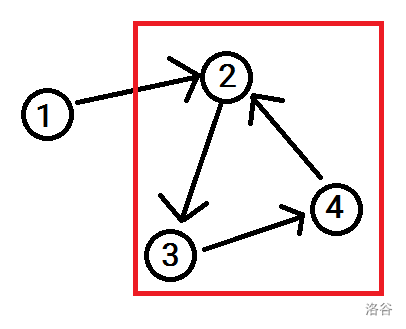
红框中显然是环。模拟其处理过程。第一次删掉了入度为 \(0\) 的 \(1\) 号节点:
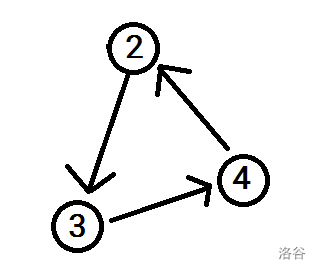
然后会发现,这时没有入度为 \(0\) 的节点可以找了,队列为空,结束 \(BFS\)。
而对于没有环的情况,所有点都是会被遍历到的。
所以,用 \(cnt\) 记录遍历过点的数量,若最后 \(cnt<n\),则说明有环。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,m,b[300005],in[300005],f[300005][26];
int ans,cnt,x,y;
string s;
vector<int> a[300005];
queue<int> q;
int main(){
scanf("%d%d",&n,&m);
cin>>s;
for(int i=1;i<=n;i++) b[i]=s[i-1]-'a',f[i][b[i]]++;
for(int i=1;i<=m;i++){
scanf("%d%d",&x,&y);
in[y]++;
a[x].push_back(y);
}
for(int i=1;i<=n;i++) if(!in[i]) q.push(i);
while(q.size()){
int k=q.front();
q.pop();
cnt++;
for(int i=0;i<a[k].size();i++){
int tmp=a[k][i];
for(int j=0;j<26;j++){
if(b[tmp]==j) f[tmp][j]=max(f[tmp][j],f[k][j]+1);
else f[tmp][j]=max(f[tmp][j],f[k][j]);
}
in[tmp]--;
if(!in[tmp]) q.push(tmp);
}
}
if(cnt<n) printf("-1");
else{
for(int i=1;i<=n;i++){
for(int j=0;j<26;j++) ans=max(ans,f[i][j]);
}
printf("%d",ans);
}
return 0;
}
0X07 P1038 [NOIP2003 提高组] 神经网络
题目没有说清楚,输入层神经元不需要减去阈值 \(u\) 。
输入 \(c,u\) 时可以直接处理,若 \(c[i]>0\),直接入队。否则就将 \(c[i]\) 减去 \(u\)(早晚都要减)。
然后就是拓扑。注意,当一个点的 \(c[i]\le 0\) 时是不会被激活的,所以直接 \(continue\)。然后按照题目给的公式,每次将 \(tmp.v\times c[t]\) 传下去即可。
最后的答案是 \(c[i]>0\) 并且出度为 \(0\) 的点(输出层)。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,m,in[105],out[105],c[105],u,x,y,w,fl;
struct node{
int to,v;
}k;
vector<node> a[105];
queue<int> q;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d%d",&c[i],&u);
if(c[i]) q.push(i);
else c[i]-=u;
}
for(int i=1;i<=m;i++){
scanf("%d%d%d",&x,&y,&w);
k.to=y,k.v=w;
in[y]++,out[x]++;
a[x].push_back(k);
}
while(q.size()){
int t=q.front();
q.pop();
if(c[t]<=0) continue;
for(int i=0;i<a[t].size();i++){
node tmp=a[t][i];
c[tmp.to]+=tmp.v*c[t];
in[tmp.to]--;
if(!in[tmp.to]) q.push(tmp.to);
}
}
for(int i=1;i<=n;i++){
if(c[i]>0&&!out[i]) printf("%d %d\n",i,c[i]),fl=1;
}
if(!fl) printf("NULL");
return 0;
}
0X08 P1137 旅行计划
和“最大食物链计数”基本相同,只要把转移改一下即可(只记到达的数量):
ans[tmp]=max(ans[tmp],ans[k]+1);
Code:
#include<bits/stdc++.h>
using namespace std;
int n,m,in[100005],x,y,ans[100005];
vector<int> a[100005];
queue<int> q;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d",&x,&y);
in[y]++;
a[x].push_back(y);
}
for(int i=1;i<=n;i++){
if(!in[i]){
ans[i]=1;
q.push(i);
}
}
while(q.size()){
int k=q.front();
q.pop();
for(int i=0;i<a[k].size();i++){
int tmp=a[k][i];
ans[tmp]=max(ans[tmp],ans[k]+1);
in[tmp]--;
if(!in[tmp]) q.push(tmp);
}
}
for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号