最小生成树之kruskal算法

定义

克鲁斯卡尔（Kruskal）算法过程：构造最小生成树（U,TE）

1. 置U的初值等于V（即包含有G中的全部顶点），TE的初值为空集（即图T中每一个顶点都构成一个连通分量）。
2. 将图G中的边按权值从小到大的顺序依次选取：
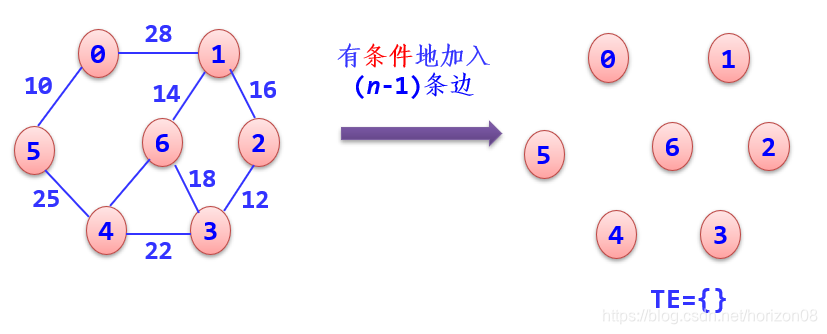
 -  若选取的边未使生成树T形成回路，则加入TE；
 -  否则舍弃，直到TE中包含(n-1)条边为止。

结构体定义

typedef struct sn
{
    int u; //当前顶点
    int v; //下一个顶点
    int w; //权值
}Edge;

Edge E[MAXV];

核心代码

kruskal算法的c语言形式

void Kruskal(MatGraph g)
{  int i,j,u1,v1,sn1,sn2,k;
   int vset[MAXV];
   Edge E[MaxSize];		//存放所有边
   k=0;				//E数组的下标从0开始计
   for (i=0;i<g.n;i++)	//由g产生的边集E
     for (j=0;j<g.n;j++)
        if (g.edges[i][j]!=0 && g.edges[i][j]!=INF)
	 {  E[k].u=i;  E[k].v=j;  E[k].w=g.edges[i][j];
	    k++;
	 }
   InsertSort(E,g.e);		//用直接插入排序对E数组按权值递增排序
   for (i=0;i<g.n;i++) 	//初始化辅助数组
	vset[i]=i;
    k=1;				//k表示当前构造生成树的第几条边
    j=0;				//E中边的下标，初值为0
while (k<g.n)		//生成的边数小于n时循环
  { 
     u1=E[j].u;v1=E[j].v;	//取一条边的头尾顶点
     sn1=vset[u1];
     sn2=vset[v1];		//分别得到两个顶点所属的集合编号
     if (sn1!=sn2)  		//两顶点属于不同的集合
     {  printf("  (%d，%d):%d\n",u1,v1,E[j].w);
        k++;		   	//生成边数增1
        for (i=0;i<g.n;i++)  	//两个集合统一编号
           if (vset[i]==sn2) 	//集合编号为sn2的改为sn1
		        vset[i]=sn1;
     }
     j++;			//扫描下一条边
  }
}

Enjoy