Google PageRank
edited from How Google Finds Your Needle in the Web's Haystack
Google搜索的核心算法当然不止是PageRank,但PageRank确实是其中的核心部分。Google就曾经说过:“the heart of our software is PageRank”.
Google的PageRank算法声称他们比较了一个月来网页的受欢迎程度从而确定哪个网页显得比较重要。根据Sergey Brin和Lawrence Page的说法,一个网页的重要性不仅仅包括他们自身的重要程度,还包括链接向这个网页的其他网页数目。
综合公式为:
![\[ I(P_i)=\sum_{P_j\in B_i} \frac{I(P_j)}{l_j} \]](http://www.ams.org/featurecolumn/images/december2006/index_1.gif)
呵呵,看到这个公式我第一反应就是,“我靠,这怎么整啊,这不是鸡生蛋,蛋生鸡”的问题吗?果然,下面就有解决办法。
我们将这个问题转化为一个数学问题。
首先构造一个链接矩阵,![$ {\bf H}=[H_{ij}] $](http://www.ams.org/featurecolumn/images/december2006/index_2.gif) 。其中:
。其中:
![\[ H_{ij}=\left\{\begin{array}{ll}1/l_{j} & \hbox{if } P_j\in B_i \\ 0 & \hbox{otherwise} \end{array}\right. \]](http://www.ams.org/featurecolumn/images/december2006/index_3.gif)
同时也创建一个向量![$ I=[I(P_i)] $](http://www.ams.org/featurecolumn/images/december2006/index_4.gif) ,它的构成正是PageRank的值,也就是页面的相对重要程度。用数学表达式定义为:
,它的构成正是PageRank的值,也就是页面的相对重要程度。用数学表达式定义为:![\[ I = {\bf H}I \]](http://www.ams.org/featurecolumn/images/december2006/index_5.gif)
这个表达式其实也就是向量 I 为矩阵特征值为1的特征向量,也称呼它为H的固定向量。
下边是一个例子:
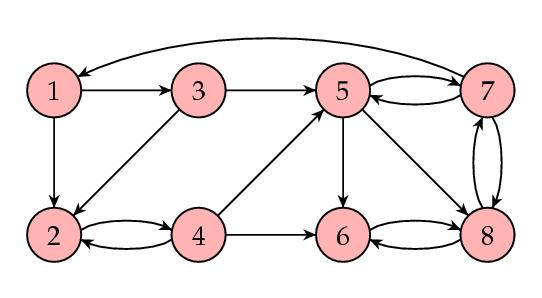

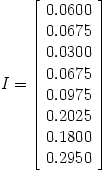
这样看来,问题貌似得到了解决,我们获得了这8个网页的PageRank值。但是在现实中,这个矩阵的n为250亿,其中的大部分值为0,实际上,研究表明每个网页链接的平均数量是10,这表明每一列只有10个数值不为0。下面我们用一个叫power method的方法来寻找矩阵的固定向量。
![\[ I^{k+1}={\bf H}I^k \]](http://www.ams.org/featurecolumn/images/december2006/index_6.gif)
|
General principle: The sequence I k will converge to the stationary vector I. |
通过这个方法解释上面的例子
| I 0 | I 1 | I 2 | I 3 | I 4 | ... | I 60 | I 61 |
| 1 | 0 | 0 | 0 | 0.0278 | ... | 0.06 | 0.06 |
| 0 | 0.5 | 0.25 | 0.1667 | 0.0833 | ... | 0.0675 | 0.0675 |
| 0 | 0.5 | 0 | 0 | 0 | ... | 0.03 | 0.03 |
| 0 | 0 | 0.5 | 0.25 | 0.1667 | ... | 0.0675 | 0.0675 |
| 0 | 0 | 0.25 | 0.1667 | 0.1111 | ... | 0.0975 | 0.0975 |
| 0 | 0 | 0 | 0.25 | 0.1806 | ... | 0.2025 | 0.2025 |
| 0 | 0 | 0 | 0.0833 | 0.0972 | ... | 0.18 | 0.18 |
| 0 | 0 | 0 | 0.0833 | 0.3333 | ... | 0.295 | 0.295 |
得到的结果只是网页重要程度的相对比值,如果要的到最终的PageRank数值,还需要对它进行线性增加,使得它们的总和为1。
有三个问题自然地就提出来了:
- I k是否会汇聚到1
- 向量是否与I0的取值无关
- 是否包含了我们想要的信息,也就是达到充分统计
现在我们对这三个问题还只能说No,但接下来我们将会修改我们的方法使得对这三个问题的回答得到肯定。
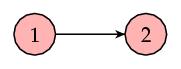 |
with matrix |
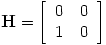 |
结果如下:
| I 0 | I 1 | I 2 | I 3=I |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
上面例子的问题是P2并没有链接,它在每次迭代中获取了P1的一些权重,但是却不传给其他网页。像这样没有链接的节点我们称它为悬挂节点,显然,真实环境中这样的网页还很多。要解决这个问题,我们可以转换一种思维方式来思考PageRank,或者说用另外一种视角。
设想我们随机的上网冲浪,我们会随机地从一个页面跳转到另外一个页面。设我们浏览的页面为Pj,它拥有j个链接,其中一个将我们链接到Pi这个页面,那么我们最终浏览Pi页面的概率为1/lj。因为是随机冲浪的,所以我们可以用时间来类比,我们是将在Pj上面浏览的一个时间碎片交给了Pi,也就是Tj/lj。如此叠加,我们可以确定Pi的时间为:
![\[ T_i = \sum_{P_j\in B_i} T_j/l_j \]](http://www.ams.org/featurecolumn/images/december2006/index_10.gif)
也就是说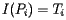 。
。
利用这种视角考虑一个没有任何链接的悬挂节点。我们不可能在这个页面上终止我们的网上冲浪,我们会随机的浏览另外一个网页,可能是通过浏览器的地址栏输入或以其他方式跳转,那么我们可以得到我们跳转向某个页面的概率为1/n,n为总的页面数。下面我们重新定义下上一个例子:
 |
with matrix |
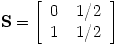 |
and eigenvector |
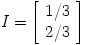 |
通常说来,power method是用来寻找矩阵特征向量对应的最大特征值的。在我们上面的例子中使用了特征值为1,实际上我们可以用比1小的特征值。 假设S的特征值为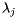 。有
。有
![\[ 1 = \lambda_1 > |\lambda_2| \geq |\lambda_3| \geq \ldots \geq |\lambda_n| \]](http://www.ams.org/featurecolumn/images/december2006/index_15.gif)
则有:
![\[ I^0 = c_1v_1+c_2v_2 + \ldots + c_nv_n \]](http://www.ams.org/featurecolumn/images/december2006/index_17.gif)
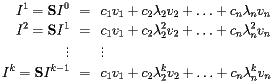
Since the eigenvalues  with
with 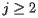 have magnitude smaller than one, it follows that
have magnitude smaller than one, it follows that 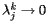 if
if 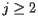 and therefore
and therefore 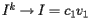 , an eigenvector corresponding to the eigenvalue 1.
, an eigenvector corresponding to the eigenvalue 1.
It is important to note here that the rate at which 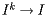 is determined by
is determined by 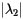 . When
. When 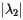 is relatively close to 0, then
is relatively close to 0, then 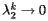 relatively quickly.
relatively quickly.
以上的讨论中,我们假设矩阵S的 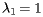 并且
并且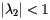 ,但实际上不常是这样的。
,但实际上不常是这样的。
下面的例子:
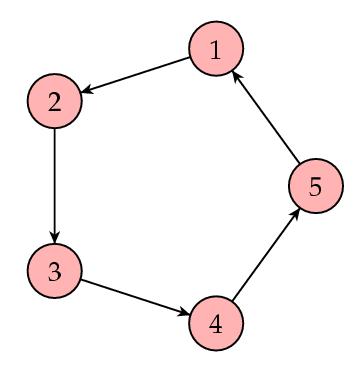
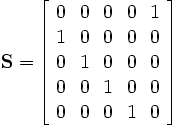
那么有
| I 0 | I 1 | I 2 | I 3 | I 4 | I 5 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 |
the sequence of vectors I k fails to converge。这是因为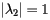 ,所以power method就失效了。
,所以power method就失效了。
为了保证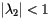 , 矩阵S 必须 primitive。 这意味着对于某个自然数m, Sm中的数值全为正。也就是说,对于两个页面,最多经过m个链接,可以从第一个页面跳转到第二个页面。显然,上个例子并不满足。
, 矩阵S 必须 primitive。 这意味着对于某个自然数m, Sm中的数值全为正。也就是说,对于两个页面,最多经过m个链接,可以从第一个页面跳转到第二个页面。显然,上个例子并不满足。
下面是另外一个例子:
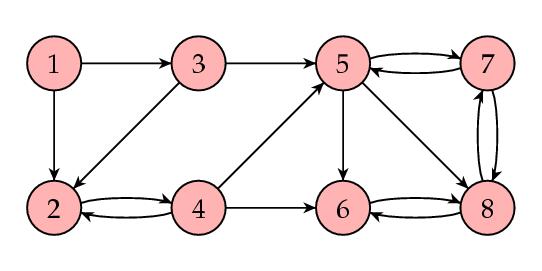
 |
with stationary vector |
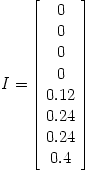 |
有4个网页的PageRank为0,这显然不对,原因是上图中内涵一个更小的网络。
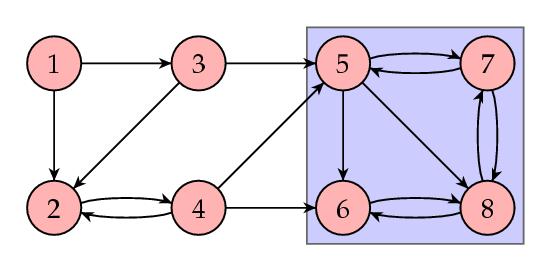
就像上面所说的悬挂节点一样,前4个页面的权值进入蓝色的区域后,就在内部消化而不返回出来,其余4个页面获得了前4个页面所有的权值。这是因为矩阵S是可约的,也就是如下形式:
![\[ S=\left[\begin{array}{cc} * & 0 \\ * & * \end{array}\right]. \]](http://www.ams.org/featurecolumn/images/december2006/index_39.gif)
要达到不可约,则网络图必须是强连通的,只有强连通图,才能保证有不可约的矩阵。
最终修改:
我们需要重新构造我们的上网行为:我们在浏览有链接的网站时,仍然有一定的几率不遵守这个网站上面的链接,而直接在地址栏上面输入我们想要去的网站,假设这个概率为 。
。
最终的公式为:![\[ {\bf G}=\alpha{\bf S}+ (1-\alpha)\frac{1}{n}{\bf 1} \]](http://www.ams.org/featurecolumn/images/december2006/index_44.gif)
显然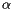 值应该要非常接近1,根据大量的实验结果,Serbey Brin和Larry Page选择了0.85。
值应该要非常接近1,根据大量的实验结果,Serbey Brin和Larry Page选择了0.85。
使用power method则公式为:
![\[ {\bf S}={\bf H} + {\bf A} \]](http://www.ams.org/featurecolumn/images/december2006/index_52.gif)
![\[ {\bf G}=\alpha{\bf H} + \alpha{\bf A} + \frac{1-\alpha}{n}{\bf 1} \]](http://www.ams.org/featurecolumn/images/december2006/index_53.gif)
![\[ {\bf G}I^k=\alpha{\bf H}I^k + \alpha{\bf A}I^k + \frac{1-\alpha}{n}{\bf 1}I^k \]](http://www.ams.org/featurecolumn/images/december2006/index_54.gif)




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步