奇异值分解 中篇

对于一个\(m{\times}n\)矩阵\(A\)，\(Ax\)表示一个从\(n\)维向量到\(m\)维向量的线性变换，那么对于\(n\)维空间中的单位超球面\(\Vert x \Vert =1\)上的所有向量\(x\)，哪一个在变换后模长最小（大）呢

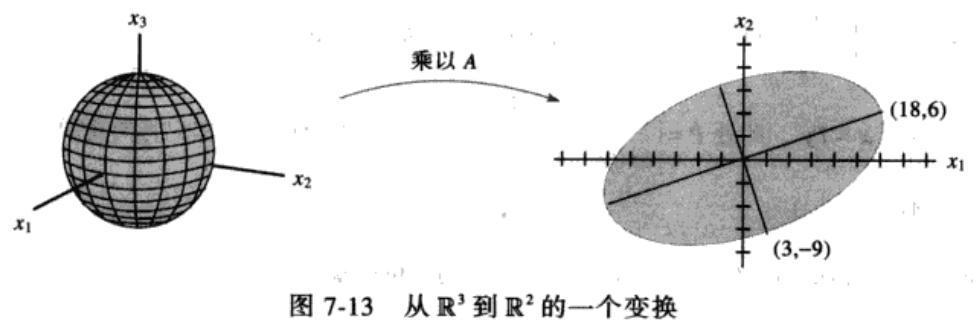
从上篇的分析可知，对于\(A^T A\)的单位特征向量\(v_i\)，有\(\Vert A v_i \Vert = \sigma_i\). 同时，由于\(A^T A\)是实对称矩阵且形状为\(n{\times}n\)，故\(A^T A\)具有\(n\)个两两正交的单位特征向量\(\{ v_1, ... , v_n \}\)（按对应特征值的降序排列），因此任意\(n\)维向量\(x\)均可表示为\(x=\sum\limits_{i=0}^{n}{k_i v_i}\)，且\(Ax=\sum\limits_{i=0}^{n}{k_i A v_i}\)

由于\(\{ v_1, ... , v_n \}\)在经过变换后依旧两两正交，因此\({\Vert Ax \Vert}^2 = (Ax)^T{Ax} = \sum\limits_{i=0}^{n}{k_i^2 (Av_i)^T{Av_i}} = \sum\limits_{i=0}^{n}{k_i^2 \sigma_i^2}\)

由于\(\Vert x \Vert ^2 = \sum\limits_{i=0}^{n}{k_i^2} = 1\)，且\(\sigma_n\)为\(A\)的最小奇异值，因此当\(x=v_n\)时，\(\Vert Ax \Vert\)模长最小，同理，当\(x=v_1\)时，\(\Vert Ax \Vert\)模长最大