反思汇总(倒续更新
有生之年系列
csp-s模拟测试59 2019-10-04
又是快乐的吃*的一天
没有借口,调不出来,就是菜。
垃圾又头铁。
A. Reverse
奇偶性质很显然,建边需要优化也很显然。
大佬都会线段树优化建边,我只能用垃圾$set$,$md$我什么脑子要左右分开跑??
处理出左右端点,把迭代器$++$移动。
这个过程在$Bfs$中做。
csp-s模拟测试58 2019-10-03
挂了$120$,男受。
没本事的垃圾就不要做$T3$了,把**$T1$,$T2$做好就完了。(自黑 $Rp++$
$T2$没打同一个时刻选择很多件。
把时间离散一下就$A$了。
$T3$边的数组没开二倍(来自刚刚开始玩前向星的$vector$玩家的怨念……
A. Divisors
水题,过了。
B. Market
也是水题,这种背包做过两次了。(但是我不会$01$背包就很难受了
把时间离散就可以打普通$DP$了(无脑
还有以后不要再拿错的数据用错的暴力拍错的“正解”了!!
题比较简单,把长龟背包的数组下标换一下就好了。
但是查询需要优化。
我们发现对于一个时间$t$价值和代价正相关。
所以把询问离线,按$t$为第一关键字排序,$M$为第二关键字排序,根据单调性,最差复杂度为$O(n^3)$,最优性和询问次数无关。
C. Dash Speed
咕咕咕
csp-s模拟测试56 2019-10-02
其实和预估分差$8$分,T1本来可以做掉的,但是忘了$nth$ _ $element$怎么拼了,所以这就是我考场玩(tui)了半个小时$Qt$的原因。
$T2$打的真爽,正解挺好想的,就是暴力打错还一直在对拍????,w tm拿正解调了半年暴力???(最后知道真相的我眼泪落下来
这次依旧放了对拍恶心身边人。($kxkx$但是好像Moudingggggggggg心态很稳QAQ。
$T3$暴力都没打,太菜了。。。。
A. Merchant
二分。$0$的时候特判一下。
B. Equation
修改操作其实只对那一棵子树产生影响。
很自然就能想到求出$dfs$序,再用树状数组单点查询,区间修改维护。
注意对儿子和孙子或者说深度奇偶产生的影响是不一样的。
我打的比较不一样,我用了好多树状数组,对于根$1$和他的直接儿子各开一个来支持以上不同影响。
还重新对深度奇偶建了新的图跑的$dfs$序。
具体实现的话,显然内存不好控制。
把树状数组的数组开成$vector$再$resize$就可以保证内存了。
其实这个题大家都应该能想到正解(但是要有耐心实现啊
C. Rectangle
咕咕咕
csp-s模拟测试(b) 2019-10-01
国庆信心赛,没有反思,没有题解。
其实还是有一点的。
就是对拍要谨慎,不然会把身边的同志心态搞炸。。。。
csp-s模拟测试55 2019-09-29
$T1$,$T2$都是正解,都因为没有底气弃掉了。
考场上$T1$把自己折磨死,一直调不出来,就打了所有部分分($woc$还没有我树状数组水不过的部分分
A. 联
水题,正解很好想,因为有$xor$,所以维护最左端的$0$和$1$就好了。
有信心有耐心$==ac$。
B. 赛
水题,枚举公共物品的思路很显然,考场上没时间了只能暴力维护。
打了一个$vis$标记,本质上是正解增增删删的思路,但是没时间,最后打挂了。
可以用动态开点,再根据情况删点增点,维护前缀和和个数就好了。
C. 题
不会,待填。
csp-s模拟测试54 2019-09-28
$T1$正解了,$T2$的记忆化打挂了,丢了$51$,就只改了一个判断位置,$T3$部分分也挂了,$-$打成了$+$,丢$14$。
以后要认真点啊,虽然这场感觉很好,算下来还是丢了不少。
A. x
水题,显然如果两个数$a$,$b$同时是一个数$x$的质因子的话,所有含有$a$或$b$的数都要放在一个集合里。所以使用并查集。加上全是$1$的部分分提示,很自然想到$2^n-2$。
B. Y
挺好的一道题。考场的记忆化暴力可以水到很多分。
正解是$bitset$,$STL$玩家表示很好$van$。
还有一个新思想(其实也不新,双向$BFS$),$meet int the middle$。
我们表示一下对于某个点$x$,是否存在一个状态$S$,可以用$bitset$将点合并,用$meet int the middle$思路优化状态数。
倒序枚举点$x$的话最后就得到了关于$x$的存在状态$g$,配合$f$数组可以合并状态。
C. Z
大概思路有了,实现起来有点困难,先咕咕咕。
csp-s模拟测试53 2019-09-27
csp-s模拟测试51(b) 2019-09-22
垃圾Smily都感觉这b组题lj
T1 A了 T3原题(还更简单了) md全场22个人A的T2********的我爆零了
****T2好水啊
****T1$Lca$调俩小时
****T3开$long double?????$
A. attack
其实$T1$还是很水了的,部分分的提示很明显,就是公共$lca$,按着拓扑序加入新的树
csp-s模拟测试50 2019-09-22
T1数组脑残开小炸掉20,T2暴力达到标准暴力分,T3无脑$n^5$暴力拿到20(c n m 以暴力为生
T2至今未改过来,(毕竟我是分块控稍微抵制莫队 但是优雅暴力一家亲啊喂 听说莫队都不用分块的,先咕着明天改
A. 施工
主要是证明那个填平不会......
$f[i]$表示考虑到$i$并且$i$这个位置高度不变的最小代价
那么转移方程就很好写了 $f[i]=\sum_{k=j+1}^{i-1}(t-h_k)^{2}+c*(h_j+h_i-2*t)+f[j]$
但是有一个细节 答案不是$f[n]$ 你需要在左右放上一个无限高的假想柱子 最后求$f[n+1]$
表示$i$从$j$转移过来,我们想什么样的$j$可以转移到$i$
一定是$j<=i$ 并且对于任意的$j+1<=k<=i-1$ 都有$h[k]<=h[i]$ $and$ $h[k]<=h[j]$
(显然啊因为你要把 $i,j$ 之间的全都往上填
我们再想 如何维护可以转移的 $j$ 的集合 我们发现如果枚举的话会使复杂度“优化”到$O(n^2)$
于是我们颓完题解选择了单调栈
想想为什么要用单调栈
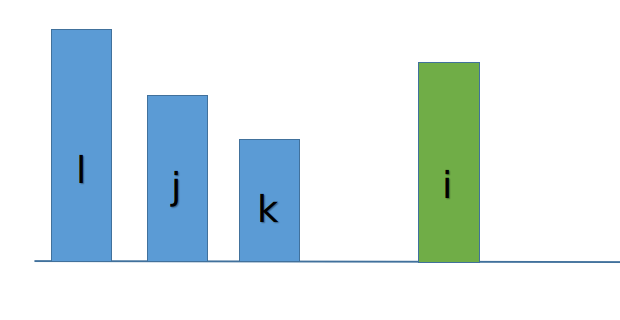
我们维护一个单调递减的单调栈 $l$,$j$,$k$是单调栈里的元素(单调栈存原序列下标就好
那么这个单调栈的实际含义为 在$l$,$j$之间没有比$h[l]$,$h[j]$大的元素
那么意思就是你的 $l$,$j$可以转移给$i$
并且当$i$入栈 它顶掉的(如本图中的$j$,$k$)一定不会转移给$i$后面的元素
其实很显然 记$i$后有一个$r$需要被更新 记转移点为$pos$那么必须满足上文说的
在$l$,$j$之间没有比$h[l]$,$h[j]$大的元素
在这儿也同理 在$pos$,$r$之间也不应该有比$h[pos]$,$h[r]$大的元素
那么我们想 被$i$顶掉的$k$显然不可能作为转移点 因为$k$和$r$之间有一个$i$使得$k$不可能作为$pos$
这是单调栈的优秀性和正确性(删除了没必要的转移点,并且删除的操作是对的
单调栈维护的转移点讨论完了,我们思考转移
我们想应该怎么转移 以一个$j$转移给$i$为例
我们要做的 是把$j+1$到$i-1$之间的填平
想数组含义 这一定是$j$,$i$不动 那么就可以代价分为到达 $j$且$j$不动的最小代价$f[j]$和填平$j+1$到$i-1$的代价
即转移方程的由来 $f[i]=\sum_{k=j+1}^{i-1}(t-h_k)^{2}+c*(h_j+h_i-2*t)+f[j]$
现在我们要做的是求一个$t$使结果最优 显然是一个二次函数的形式
假设我们拥有了二次函数的最低点对应的$t$
我们想即便是高考数学上你也要保证自变量$t$符合实际情况
那么我们的$t$呢
一定要比$h[i]$,$h[j]$小 并且比$max(h[k])$,$j+1<=k<=i-1$大
即对于求出来的最优(不一定符合实际)的$t$设限制
显然最后对于$h[i]$,$h[j]$取$min$,对于$max(h[k])$取$max$就好
$h[i]$,$h[j]$已知,那$max(h[k])$呢?
想想单调栈 记栈顶为$top$
显然$i$和$top-1$之间的最大值是$h[top]$
所以可以每次在弹栈前进行修改
以$top-1$为$j$,$h[top]$为$max(h[k])$更新答案 然后把$top$弹走 这时我们是不用考虑$top-1$的
关于$t$的求法 就是二次函数最低点$-b/2a$
把原始方程化为$a*t^2+b*t+c$的形式 求出$t$ 并如上设限带入求值就好
$t=-\tfrac{b}{2a}=\tfrac{\sum_{k=j+1}^{i-1}h_k+c}{(i-1-j)}$
注意边界问题 在我们假象的柱子上是不用付出代价的(比如你当前要转移到$n+1$ 把之前的填为$t$ 是不需要付出$(h[n+1]-t)*c$的代价的)
大体就是这样 但是证明为什么是平的我只能YY
B. 蔬菜
我正在打莫队
我打完莫队了

C. 联盟
$O(n^5)$暴力有人听吗?

我打的是错解我非人
首先找出直径,如果直径唯一的话,那条断边一定在直径上选。
因为你选择其他边的话 直径还是做了最大的负贡献
好因为测试点太水我们就快乐的选择不打正解利用了这个性质
(至于为什么会只有一条直径,可能是良(×)心(×)出题人的特殊数据,如果有两条的话好像第三问就没有意义了,意思就是他为了防止被人水掉第三问的分而白白送了我们$50$分 $QwQ$)
所以我们枚举直径上的边 断成两坨子树 在两坨子树里求子树直径
那么对于这种断边情况 它的候选答案$tmp$是$max((len_x/2+len_y/2+1),len_x,len_y)$
然后在用$tmp$更新$ans$ $ans=min(ans,tmp)$
想想Dp求树的直径的数组定义 是不是表示到达这个节点后的最长长度?(就是$ans$一直取$max$的操作
但是它是对于整棵树说的 我们要的是针对一棵子树 不能直接搬用 $Dp$需要略改一手 不再赘述
所以可以正反两遍$dfs$ 求出前缀直径 和 后缀直径
再在直径上枚举更新答案 第一二问就快乐的做了出来
第三问也简单 (先咕着
我又来更了......
其实也没啥了,我的$sb$算法.....
第二问求出来可以干掉哪条边,就直接从里边随便拿一条,断掉,记录端点为$st$和$ed$,用$st$和$ed$分别再跑树的直径,然后分别把以$st$和$ed$为根的各自的直径上的点集处理出来,再各自取点集中点输出就好。


