20190718
我是一如既往的弱。
T1. 星际旅行
很简单的一道乱搞题。
将所有的边拆成两条,问题变成去掉两条边,使得原图存在一条欧拉路
径。注意新图中所有点的度数均为偶数,只需按照去掉任意2个自环、去掉任
意1个自环和任意一条边、去掉两条有公共顶点的边进行讨论即可。注意图不连
通的判断方式,不是点不连通,而是边不连通。
标准题解说是要把无向边拆为两条有向边,那么问题就转化为去掉两条边使得原图存在一条欧拉路径。
要保证新图中所有点的度数都为偶数
我们先考虑两种简单情况
1. 删除任意两个自环 即 ans+=sum(be_back)*(sum(be_back)-1)/2;
2. 删除任意一个自环和一条边 即 ans+=m(处自环外的路径 双向边单向注意*2)*sum(back);
还有就是删除两条路径
我们考虑怎样删除可以使得所有点的度数为偶 显然是删除连接着同一个点的两条边
具体点呢?
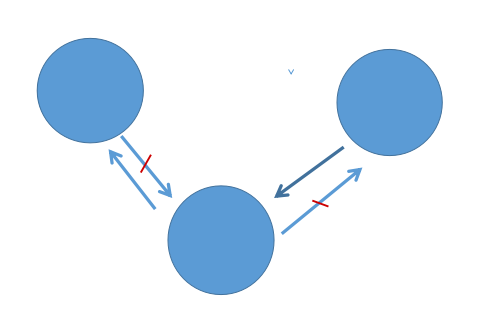
删除如图所示的两条即可
用语言描述出来就是一条入边一条出边
对于一个点方案数为 C(入度,1)*(C(出度,1) -1)
记 入度或者出度为in 即in*(in-1) (式1)
为什么要减一呢 因为你不能同时把原来的一条完整的无向边完全砍掉
但是式1要除2 见 样例说明 (第七条路径与第一条不同)
然后可以快乐的提交了
题目很坑 要判边联通
值得一提的是可以选择并查集 效率很高
但是判断条件有点繁琐 一是存在两个大小>=2的集合 二是一个单独的点里有自环
数据还是很棒的

#include <vector> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; #define QAQ 100110 #define re register #define ll long long #define max(a,b) ( (a) > (b) ) ? (a) : (b) #define min(a,b) ( (a) < (b) ) ? (a) : (b) #define fup(i,a,b) for(re int i=a;i<=b;++i) #define fdn(i,a,b) for(re int i=a;i>=b;--i) int fa[QAQ],in[QAQ],fu[QAQ]; int n,m,be_back,sum; bool judge[QAQ]; ll ans; inline ll read(){ re ll x(0),f(1);re char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();} return x*f; } int find(re int x){ return x==fa[x]?x:fa[x]=find(fa[x]); } inline void merge(re int x,re int y){ x=find(x),y=find(y); fa[x]=y; } int main(){ n=read(),m=read(); fup(i,1,n)fa[i]=i; fup(i,1,m){ re int x,y; x=read(),y=read(); if(x==y){ judge[x]=1; ++be_back; } else { merge(x,y); ++in[x]; ++in[y]; ++sum; } } fup(i,1,n)++fu[find(i)]; bool flag=0; fup(i,1,n){ if(fu[i]==1&&judge[i]){ puts("0"); return 0; } if(fu[i]>=2){ if(!flag)flag=1; else { puts("0"); return 0; } } } fup(i,1,n)ans+=1ll*(in[i]-1)*in[i]/2; ans+=1ll*be_back*(be_back-1)/2; ans+=1ll*be_back*sum; printf("%lld",ans); }
T2.砍树
不要二分!不要二分!!不要二分!!!
其实并不难,比如soul大神A掉了
问题等价于求一个最大的d,满足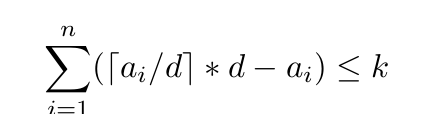 \
\
移项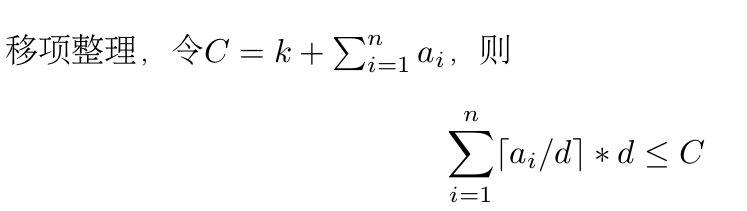
然后把d除过去
(不会打 sigma 只能截题解QAQ)具体细节还是有点东西的
右边就变成了 C/d 向下取整
(联系数学函数 使 左边最大 小于 右边最小 则一定恒成立)
左右都是单调递减(非严格)
可以发现随着d的增大 左边的变化频率比较快 右边比较慢
 (蓝色为右,红色为左)
(蓝色为右,红色为左)
为什么呢,其实很显然
左边相当与先有误差后把误差加和 右边只有一次误差 左边会把误差放大
可以手模几组例子
如 3/2-> 2 5/2->3 7/2->4
但 3/3-> 1 5/3->2 7/3->3
而右边 (3+5+7+8888888)== (3+5+7+8888888)/3
显然左边变化大
下面定义的区间指的是d的取值范围
对于每一个右边的区间 l->r 右边的值是不变的
而左边在疯狂变化
但是有单调性 即若式子在l可行那么整个 l->r 都可行
同时 r 处不可行则整个区间都不行
换言之,最优解在 r 处(如果中间交点处mid可行 那么r也可行 再换言之 若不行 则一定是在r出先开始)
即暴力验证 r 处的 d 大小是否合适
注意区间的范围就好了

1 #include <vector> 2 #include <cstdio> 3 #include <cstring> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 #define QAQ 100110 8 #define re register 9 #define ll long long 10 #define max(a,b) ( (a) > (b) ) ? (a) : (b) 11 #define min(a,b) ( (a) < (b) ) ? (a) : (b) 12 #define fup(i,a,b) for(re int i=a;i<=b;++i) 13 #define fdn(i,a,b) for(re int i=a;i>=b;--i) 14 inline ll read(){ 15 re ll x(0),f(1);re char ch=getchar(); 16 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 17 while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();} 18 return x*f; 19 } 20 int a[QAQ]; 21 ll k,ans; 22 int n; 23 int main(){ 24 ll sum=0,minn=888888888,maxx=0; 25 n=read(),k=read(); 26 fup(i,1,n)a[i]=read(),sum+=a[i]; 27 sum+=k; 28 ll d=0; 29 while(1){ 30 if(sum/(d+1)==0)break; 31 d=sum/(sum/(d+1)); 32 re ll can=0; 33 fup(i,1,n){ 34 ll tot=a[i]/d; 35 if(a[i]%d)++tot; 36 can+=tot*d; 37 } 38 if(can<=sum)ans=d; 39 } 40 printf("%lld",ans); 41 }
T3.超级树
题解太棒了!!!
主要还是如何想到这种鬼畜的状态数组定义
数言蔽之
1.分析维度 考虑转移可能性
2.分析时间,空间复杂度
3.注意各个元素间的“公平”(很难描述,但是各个数据间确实有着微妙的联系,在以后的矩阵乘,dp中会多解释)

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #define Maxn 3050 5 #define max(x,y) ((x)>(y)?(x):(y)) 6 #define Reg register 7 using namespace std; 8 long long sum,n,mod,dp[Maxn][Maxn]; 9 int main() 10 { 11 scanf("%lld%lld",&n,&mod); 12 dp[1][1]=dp[1][0]=1; 13 for(Reg int i=1;i<=n-1;++i) 14 { 15 for(Reg int j=0;j<=n-i+2;++j) 16 { 17 for(Reg int k=0;k<=n-i+2-j;++k) 18 { 19 sum=(dp[i][j]*dp[i][k])%mod; 20 dp[i+1][j+k]=(dp[i+1][j+k]+sum)%mod; 21 //选j+k条路径 左和右分别选的贡献 22 dp[i+1][j+k+1]=(dp[i+1][j+k+1]+sum)%mod; 23 //选j+k+1条路径 左和右分别选+选根的贡献 24 dp[i+1][j+k]=(dp[i+1][j+k]+sum*2*(j+k))%mod; 25 //选j+k条路径 左(和右)分别选一条边(起点或终点)连到根的贡献 26 if(j+k-1>=0) dp[i+1][j+k-1]=(dp[i+1][j+k-1]+sum*j*k*2)%mod; 27 //选j+k-1条路径 左(右)选一条边到根在连右(左)的贡献 28 if(j+k-1>=0) dp[i+1][j+k-1]=(dp[i+1][j+k-1]+sum*(j*j-j+k*k-k))%mod; 29 //选j+k-1条路径 左(右)连根再连左(右)的贡献 30 } 31 } 32 } 33 printf("%lld",dp[n][1]%mod); 34 return 0; 35 }
总体来说吧 我考的狗屁不是 不分析算法正确性(二分,最小生成树) 把题考虑太难(礼物,通讯,星际旅行)
心态也很爆炸 中间一段时间根本什么都没码
加油吧 lz爬也要爬到第一机房
Fighting!



