第十章：树

二叉树的先中后层遍历！！！

 1 package LeetCode.test5_sousuosuanfa.Demo;
 2 
 3 public class BTree {
 4     public static void main(String[] args) {
 5         String[] root = {"1", "2", "3", null, "5"};
 6         int index = 0;
 7         TreeNode bt = createBTree(root, index);
 8         System.out.println("先序遍历：");
 9         PreOrder(bt);
10 
11         System.out.println("\n中序遍历：");
12         InOrder(bt);
13 
14         System.out.println("\n后序遍历：");
15         PostOrder(bt);
16     }
17 
18     public static class TreeNode {
19         int val;
20         TreeNode left;
21         TreeNode right;
22 
23         TreeNode() {
24         }
25 
26         TreeNode(int val) {
27             this.val = val;
28         }
29 
30         TreeNode(int val, TreeNode left, TreeNode right) {
31             this.val = val;
32             this.left = left;
33             this.right = right;
34         }
35     }
36 
37     public static TreeNode createBTree(String[] root, int index) {
38         TreeNode rootNode;   // 定义根节点
39         if (index >= root.length || root[index] == null) {
40             return null;
41         }
42         rootNode = new TreeNode(Integer.parseInt(root[index]));  // 根节点
43         rootNode.left = createBTree(root, 2 * index + 1);  // 递归建立左孩子结点
44         rootNode.right = createBTree(root, 2 * index + 2);  // 递归建立右孩子结点
45         return rootNode;
46     }
47 
48     public static void PreOrder(TreeNode root) {
49         if (root == null)
50             return;
51         System.out.print(root.val + " ");
52         PreOrder(root.left);
53         PreOrder(root.right);
54     }
55 
56     public static void InOrder(TreeNode root) {
57         if (root == null)
58             return;
59         InOrder(root.left);
60         System.out.print(root.val + " ");
61         InOrder(root.right);
62     }
63 
64     public static void PostOrder(TreeNode root) {
65         if (root == null)
66             return;
67         PostOrder(root.left);
68         PostOrder(root.right);
69         System.out.print(root.val + " ");
70     }
71 }

public class Solution {
    public ArrayList<ArrayList<Integer>> levelOrder (TreeNode root) {
        ArrayList<ArrayList<Integer>> result = new ArrayList<>();
        if(root == null){
            return result;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            ArrayList<Integer> res = new ArrayList<>();
            int size = queue.size();
            for(int i = 0; i < size; i++){
                TreeNode top = queue.poll();
                res.add(top.val);
                if(top.left!=null){
                    queue.offer(top.left);
                }
                if(top.right!=null){
                    queue.offer(top.right);
                }
            }
            result.add(res);
        }
        return result;
    }
}

一、树的递归

1、二叉树的最大深度

问题：

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

 1 package LeetCode.test10_shu;
 2 
 3 public class ques_104_二叉树的最大深度 {
 4     int max;
 5 
 6     public int maxDepth(TreeNode root) {
 7         if (root != null) {
 8             max = Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
 9         } else {
10             max = 0;
11         }
12         return max;
13     }
14 }
15 
16 class Test_104 {
17     public static void main(String[] args) {
18         String[] root = {"3", "9", "20", null, null, "15", "7"};
19         int index = 0;
20         TreeNode bt = createBTree(root, index);
21 //        PreOrder(bt);
22         ques_104_二叉树的最大深度 s = new ques_104_二叉树的最大深度();
23         System.out.println(s.maxDepth(bt));
24     }
25 
26     public static TreeNode createBTree(String[] root, int index) {
27         TreeNode rootNode;
28         if (index >= root.length || root[index] == null) {
29             return null;
30         }
31         rootNode = new TreeNode(Integer.parseInt(root[index]));
32         rootNode.left = createBTree(root, 2 * index + 1);
33         rootNode.right = createBTree(root, 2 * index + 2);
34         return rootNode;
35     }
36 
37     public static void PreOrder(TreeNode root) {
38         if (root == null)
39             return;
40         System.out.print(root.val + " ");
41         PreOrder(root.left);
42         PreOrder(root.right);
43     }
44 }

View Code

2、平衡二叉树

问题：

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：true
示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false
示例 3：

输入：root = []
输出：true

 1 package LeetCode.test10_shu;
 2 
 3 /**
 4  * 思路：类似于后序遍历，对于当前遍历到的节点，先递归地判断其左右子树是否平衡，再判断以当前节点为根的子树是否平衡。
 5  * 如果一棵子树是平衡的，则返回其高度（高度一定是非负整数），否则返回−1。如果存在一棵子树不平衡，则整个二叉树一定不平衡。
 6  */
 7 public class ques_110_平衡二叉树 {
 8     public boolean isBalanced(TreeNode root) {
 9         return getDepth(root) != -1;
10     }
11 
12     private int getDepth(TreeNode root) {
13         if (root == null) {
14             return 0;
15         }
16         int left = getDepth(root.left);  // 判断左子树是否是平衡的  -1或高度
17         int right = getDepth(root.right);// 判断右子树是否是平衡的  -1或高度
18         if (left == -1 || right == -1 || Math.abs(left - right) > 1) {
19             return -1;
20         } else {
21             return Math.max(left, right) + 1;
22         }
23     }
24 }
25 
26 class Test_110 {
27     public static void main(String[] args) {
28 //        String[] root = {"3", "9", "20", null, null, "15", "7"};
29 //        String[] root = {"1", "2", "2", "3", "3", null, null, "4", "4"};
30 //        String[] root = {"1", "2", "2", "3", null, null, "3", "4", null, null, "4"};
31         String[] root = {"1", "2", "2", "3", null, null, "3", "4", null, null, null, null, null, null, "4"};
32 //        String[] root = {};
33         int index = 0;
34         TreeNode bt = createBTree(root, index);
35         PreOrder(bt);
36         ques_110_平衡二叉树 s = new ques_110_平衡二叉树();
37 //        System.out.println(s.isBalanced(bt));
38     }
39 
40     public static TreeNode createBTree(String[] root, int index) {
41         TreeNode rootNode;
42         if (index >= root.length || root[index] == null) {
43             return null;
44         }
45         rootNode = new TreeNode(Integer.parseInt(root[index]));
46         rootNode.left = createBTree(root, 2 * index + 1);
47         rootNode.right = createBTree(root, 2 * index + 2);
48         return rootNode;
49     }
50 
51     public static void PreOrder(TreeNode root) {
52         if (root == null)
53             return;
54         System.out.print(root.val + " ");
55         PreOrder(root.left);
56         PreOrder(root.right);
57     }
58 }

View Code

 1 public class Solution {
 2     public boolean IsBalanced_Solution(TreeNode root) {
 3         if(root == null){
 4             return true;
 5         }
 6         if(Math.abs(high(root.left)-high(root.right))<=1&&IsBalanced_Solution(root.left)&&IsBalanced_Solution(root.right)){
 7             return true;
 8         }
 9         return false;
10     }
11     
12     public int high(TreeNode root){
13         if(root == null){
14             return 0;
15         }
16         return Math.max(high(root.left),high(root.right))+1;
17     }
18 }

View Code

补：

问题：判断是不是完全二叉树

给定一个二叉树，确定他是否是一个完全二叉树。

完全二叉树的定义：若二叉树的深度为 h，除第 h 层外，其它各层的结点数都达到最大个数，第 h 层所有的叶子结点都连续集中在最左边，这就是完全二叉树。（第 h 层可能包含 [1~2h] 个节点）

示例 1：

输入：{1,2,3,4,5,6}
输出：true

示例 2：

输入：{1,2,3,4,5,6,7}
输出：true

示例 3：

输入：{1,2,3,4,5,#,6}
输出：false

 1 import java.util.*;
 2 
 3 public class Solution {
 4     public boolean isCompleteTree (TreeNode root) {
 5         // write code here
 6         if(root == null){
 7             return true;
 8         }
 9         Queue<TreeNode> queue = new LinkedList<>();
10         queue.offer(root);
11         TreeNode top;
12         boolean flag = false;
13         while(!queue.isEmpty()){   
14             top = queue.poll();
15             if(top == null){
16                 flag = true;
17                 continue;
18             }
19             if(flag){
20                 return false;
21             }
22             queue.offer(top.left);
23             queue.offer(top.right);
24         }
25         return true;
26     }
27 }

View Code

3、二叉树的直径

问题：

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

示例 :
给定二叉树[1,2,3,4,5]

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

注意：两结点之间的路径长度是以它们之间边的数目表示。

 1 package LeetCode.test10_shu;
 2 
 3 /**
 4  * 思路：假设该节点的左儿子向下遍历经过最多的节点数L（即以左儿子为根的子树的深度）和其右儿子向下遍历经过最多的节点数R
 5  * （即以右儿子为根的子树的深度），那么以该节点为起点的路径经过节点数的最大值即为L+R+1。
 6  */
 7 public class ques_543_二叉树的直径 {
 8     int ans = -1;
 9 
10     public int diameterOfBinaryTree(TreeNode root) {
11         getDepth(root);
12         return ans-1;
13     }
14 
15     public int getDepth(TreeNode root) {
16         if (root == null) {
17             return 0;
18         }
19         int left = getDepth(root.left);  // 2
20         int right = getDepth(root.right); // 1
21         ans = Math.max(ans, left + right + 1);
22         return Math.max(left, right) + 1;
23     }
24 }
25 
26 class Test_543 {
27     public static void main(String[] args) {
28         String[] root = {"1", "2", "3", "4", "5"};
29         int index = 0;
30         TreeNode bt = createBTree(root, index);
31         ques_543_二叉树的直径 s = new ques_543_二叉树的直径();
32         System.out.println(s.diameterOfBinaryTree(bt));
33     }
34 
35     public static TreeNode createBTree(String[] root, int index) {
36         TreeNode rootNode;
37         if (index >= root.length || root[index] == null) {
38             return null;
39         }
40         rootNode = new TreeNode(Integer.parseInt(root[index]));
41         rootNode.left = createBTree(root, 2 * index + 1);
42         rootNode.right = createBTree(root, 2 * index + 2);
43         return rootNode;
44     }
45 }

View Code

4、路径总和III

问题：

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。
示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

 1 package LeetCode.test10_shu;
 2 
 3 /**
 4  * 思路：如果选取该节点加入路径，则之后必须继续加入连续节点，或停止加入节点；如果不选取该节点加入路径，则对其左右节点进行重新进行考虑。
 5  */
 6 public class ques_437_路径总和III {
 7     public int pathSum(TreeNode root, int targetSum) {
 8         if (root == null) {
 9             return 0;
10         }
11         return pathSumStartWithRoot(root, targetSum) + pathSum(root.left, targetSum) + pathSum(root.right, targetSum);
12     }
13 
14     private int pathSumStartWithRoot(TreeNode root, int targetSum) {
15         // 用来计算连续加入节点的路径
16         if (root == null) {
17             return 0;
18         }
19         int count;
20         if (root.val == targetSum) {
21             count = 1;  //找到了1条路径
22         } else {
23             count = 0; //没有找到
24         }
25         count += pathSumStartWithRoot(root.left, targetSum - root.val);
26         count += pathSumStartWithRoot(root.right, targetSum - root.val);
27         return count;
28     }
29 
30     private void PreOrder(TreeNode root) {
31         if (root == null)
32             return;
33         System.out.print(root.val + " ");
34         PreOrder(root.left);
35         PreOrder(root.right);
36     }
37 }
38 
39 class Test_437 {
40     public static void main(String[] args) {
41         String[] root = {"10", "5", "-3", "3", "2", null, "11", "3", "-2", null, "1"};
42         int index = 0;
43         int targetSum = 8;
44         TreeNode bt = createBTree(root, index);
45         ques_437_路径总和III s = new ques_437_路径总和III();
46         System.out.println(s.pathSum(bt, targetSum));
47     }
48 
49     public static TreeNode createBTree(String[] root, int index) {
50         TreeNode rootNode;
51         if (index >= root.length || root[index] == null) {
52             return null;
53         }
54         rootNode = new TreeNode(Integer.parseInt(root[index]));
55         rootNode.left = createBTree(root, 2 * index + 1);
56         rootNode.right = createBTree(root, 2 * index + 2);
57         return rootNode;
58     }
59 }

View Code

补：

问题：二叉树中和为某一值的路径(一)

给定一个二叉树root和一个值 sum ，判断是否有从根节点到叶子节点的节点值之和等于 sum 的路径。

示例 1：

输入：{5,4,8,1,11,#,9,#,#,2,7},22
输出：true

示例 2：

输入：{1,2},0
输出：false

示例 3：

输入：{},0
输出：false

 1 import java.util.*;
 2 
 3 public class Solution {
 4     public boolean hasPathSum (TreeNode root, int sum) {
 5         // write code here
 6         if(root == null){
 7             return false;
 8         }
 9         if(root.left==null&&root.right==null&&root.val==sum){
10             return true;
11         }
12         return hasPathSum(root.left,sum-root.val)||hasPathSum(root.right,sum-root.val);
13     }
14 }

View Code

5、对称二叉树

问题：

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true
示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

 1 package LeetCode.test10_shu;
 2 
 3 public class ques_101_对称二叉树 {
 4     public boolean isSymmetric(TreeNode root) {
 5         if (root == null) {
 6             return true;
 7         }
 8         return isSymmetric(root.left, root.right);
 9     }
10 
11     private boolean isSymmetric(TreeNode left, TreeNode right) {
12         if (left == null && right == null) { // 如果两个子树都为空指针，则它们相等或对称
13             return true;
14         }
15         if (left == null || right == null) { // 如果两个子树只有一个为空指针，则它们不相等或不对称
16             return false;
17         }
18         if (left.val != right.val) { // 如果两个子树根节点的值不相等，则它们不相等或不对称
19             return false;
20         }
21         return isSymmetric(left.left, right.right) && isSymmetric(left.right, right.left);
22     }
23 }
24 
25 class Test_101 {
26     public static void main(String[] args) {
27 //        String[] root = {"1", "2", "2", "3", "4", "4", "3"};
28         String[] root = {"1", "2", "2", null, "3", null, "3"};
29         int index = 0;
30         TreeNode bt = createBTree(root, index);
31         ques_101_对称二叉树 s = new ques_101_对称二叉树();
32         System.out.println(s.isSymmetric(bt));
33     }
34 
35     public static TreeNode createBTree(String[] root, int index) {
36         TreeNode rootNode;
37         if (index >= root.length || root[index] == null) {
38             return null;
39         }
40         rootNode = new TreeNode(Integer.parseInt(root[index]));
41         rootNode.left = createBTree(root, 2 * index + 1);
42         rootNode.right = createBTree(root, 2 * index + 2);
43         return rootNode;
44     }
45 }

View Code

6、删点成林

问题：

给出二叉树的根节点 root，树上每个节点都有一个不同的值。

如果节点值在 to_delete 中出现，我们就把该节点从树上删去，最后得到一个森林（一些不相交的树构成的集合）。

返回森林中的每棵树。你可以按任意顺序组织答案。

示例 1：

输入：root = [1,2,3,4,5,6,7], to_delete = [3,5]
输出：[[1,2,null,4],[6],[7]]
示例 2：

输入：root = [1,2,4,null,3], to_delete = [3]
输出：[[1,2,4]]

 1 package LeetCode.test10_shu;
 2 
 3 import java.util.ArrayList;
 4 import java.util.List;
 5 
 6 public class ques_1110_删点成林 {
 7     public List<TreeNode> delNodes(TreeNode root, int[] to_delete) {
 8         List<TreeNode> temp = new ArrayList<>();
 9         List<Integer> delete = new ArrayList<>();
10         for (Integer del : to_delete) {
11             delete.add(del);
12         }
13         TreeNode endRoot = deleteNode(root, delete, temp); // 返回的是最初的根节点
14         if (endRoot != null) {
15             temp.add(endRoot);
16         }
17         return temp;
18     }
19 
20     private TreeNode deleteNode(TreeNode root, List<Integer> delete, List<TreeNode> temp) { //自底而上判断
21         if (root == null) {
22             return root;
23         }
24         root.left = deleteNode(root.left, delete, temp);   // [3,null,null]  root.left = null  root = 3
25         root.right = deleteNode(root.right, delete, temp);
26         if (delete.contains(root.val)) {
27             if (root.left != null) {
28                 temp.add(root.left);
29             }
30             if (root.right != null) {
31                 temp.add(root.right);
32             }
33             root = null;
34         }
35         return root;
36     }
37 }
38 
39 class Test_1110 {
40     public static void main(String[] args) {
41         String[] root = {"1", "2", "3", "4", "5", "6", "7"};
42         int[] to_delete = {3, 5};
43         int index = 0;
44         TreeNode bt = createBTree(root, index);
45         ques_1110_删点成林 s = new ques_1110_删点成林();
46         System.out.println(s.delNodes(bt, to_delete));
47     }
48 
49     public static TreeNode createBTree(String[] root, int index) {
50         TreeNode rootNode;
51         if (index >= root.length || root[index] == null) {
52             return null;
53         }
54         rootNode = new TreeNode(Integer.parseInt(root[index]));
55         rootNode.left = createBTree(root, 2 * index + 1);
56         rootNode.right = createBTree(root, 2 * index + 2);
57         return rootNode;
58     }
59 }

View Code

二、层次遍历

7、二叉树的层平均值

问题：

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[3.00000,14.50000,11.00000]
解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。
示例 2:

输入：root = [3,9,20,15,7]
输出：[3.00000,14.50000,11.00000]

 1 package LeetCode.test10_shu;
 2 
 3 import java.util.ArrayList;
 4 import java.util.LinkedList;
 5 import java.util.List;
 6 import java.util.Queue;
 7 
 8 public class ques_637_二叉树的层平均值 {
 9     public List<Double> averageOfLevels(TreeNode root) {
10         List<Double> temp = new ArrayList<>();
11         Queue<TreeNode> queue = new LinkedList<>();
12         if (root == null) {
13             return temp;
14         }
15         queue.offer(root);
16         while (!queue.isEmpty()) {
17             int size = queue.size();
18             double sum = 0;
19             for (int i = 0; i < size; i++) {
20                 TreeNode top = queue.poll();
21                 assert top != null;
22                 sum += top.val;
23                 if (top.left != null) {
24                     queue.offer(top.left);
25                 }
26                 if (top.right != null) {
27                     queue.offer(top.right);
28                 }
29             }
30             temp.add(sum / size);
31         }
32         return temp;
33     }
34 }
35 
36 class Test_637 {
37     public static void main(String[] args) {
38         String[] root = {"3", "9", "20", null, null, "15", "7"};
39 //        String[] root = {};
40         int index = 0;
41         TreeNode bt = createBTree(root, index);
42         ques_637_二叉树的层平均值 s = new ques_637_二叉树的层平均值();
43         System.out.println(s.averageOfLevels(bt));
44     }
45 
46     public static TreeNode createBTree(String[] root, int index) {
47         TreeNode rootNode;
48         if (index >= root.length || root[index] == null) {
49             return null;
50         }
51         rootNode = new TreeNode(Integer.parseInt(root[index]));
52         rootNode.left = createBTree(root, 2 * index + 1);
53         rootNode.right = createBTree(root, 2 * index + 2);
54         return rootNode;
55     }
56 }

View Code

三、前中后序遍历

8、从前序与中序遍历序列构造二叉树

问题：

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

 1 package LeetCode.test10_shu;
 2 
 3 /**
 4  * 思路：
 5  * 先序 pre1(root)  pre2 ... prek   prek+1 ... pren
 6  *       根节点         左子树             右子树
 7  * 后序 in1 ... ink-1  ink(root)  ink+1 ... inn
 8  *         左子树        根节点        右子树
 9  */
10 public class ques_105_从前序与中序遍历序列构造二叉树 {
11     public TreeNode buildTree(int[] preorder, int[] inorder) {
12         int len = preorder.length;
13         int preL = 0, preR = len - 1;
14         int inL = 0, inR = len - 1;
15 //        TreeNode root = createBTree(preL, preR, inL, inR, preorder, inorder);
16 //        PreOrder(root);
17         return createBTree(preL, preR, inL, inR, preorder, inorder);
18     }
19 
20     private TreeNode createBTree(int preL, int preR, int inL, int inR, int[] preorder, int[] inorder) {
21         if (preL > preR) {
22             return null;
23         }
24         TreeNode root = new TreeNode(preorder[preL]);
25         int k;
26         for (k = inL; k <= inR; k++) {
27             if (inorder[k] == preorder[preL]) {
28                 break;
29             }
30         }
31         int len = k - inL;
32         root.left = createBTree(preL + 1, preL + len, inL, k - 1, preorder, inorder);
33         root.right = createBTree(preL + len + 1, preR, k + 1, inR, preorder, inorder);
34         return root;
35     }
36 
37     private void PreOrder(TreeNode root) {
38         if (root == null)
39             return;
40         System.out.print(root.val + " ");
41         PreOrder(root.left);
42         PreOrder(root.right);
43     }
44 }
45 
46 class Test_105 {
47     public static void main(String[] args) {
48         int[] preorder = {3, 9, 20, 15, 7};
49         int[] inorder = {9, 3, 15, 20, 7};
50         ques_105_从前序与中序遍历序列构造二叉树 s = new ques_105_从前序与中序遍历序列构造二叉树();
51         System.out.println(s.buildTree(preorder, inorder));
52     }
53 }

View Code

四、二叉查找树

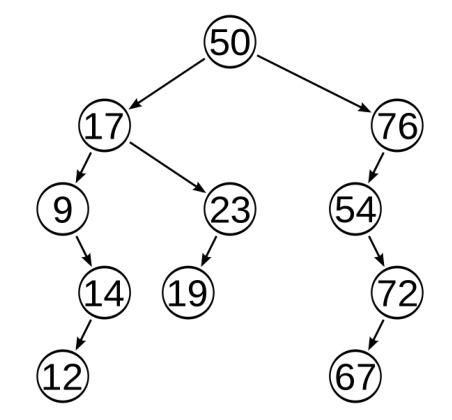
demo

  1 package LeetCode.test10_shu;
  2 
  3 /**
  4  * 二叉查找树
  5  */
  6 public class demo {
  7     public TreeNode search(TreeNode root, int x) { //查找
  8         if (root == null) {
  9             System.out.println("查找失败！");
 10             return null;
 11         }
 12         if (x < root.val) {
 13             return search(root.left, x);
 14         }
 15         if (x > root.val) {
 16             return search(root.right, x);
 17         }
 18         System.out.println("查找成功！");
 19         return root;
 20     }
 21 
 22     public TreeNode insert(TreeNode root, int x) { //插入
 23         if (root == null) {
 24             root = new TreeNode(x);  //新建节点
 25         } else if (x < root.val) {
 26             root.left = insert(root.left, x);
 27         } else if (x > root.val) {
 28             root.right = insert(root.right, x);
 29         }
 30         return root;
 31     }
 32 
 33     public TreeNode create(int[] data) { //建立二叉树
 34         TreeNode root = null;
 35         for (int i = 0; i < data.length; i++) {
 36             root = insert(root, data[i]);
 37         }
 38         return root;
 39     }
 40 
 41     public TreeNode findMax(TreeNode root) {
 42         if (root == null || root.right == null) {
 43             return root;
 44         }
 45         return findMax(root.right);
 46     }
 47 
 48     public TreeNode findMin(TreeNode root) {
 49         if (root == null || root.left == null) {
 50             return root;
 51         }
 52         return findMin(root.left);
 53     }
 54 
 55     public TreeNode remove(TreeNode root, int x) {  //删除
 56         if (root == null) {
 57             return null;
 58         }
 59         if (root.val == x) {
 60             if (root.left == null && root.right == null) { //叶子节点直接删除
 61                 root = null;
 62             } else if (root.left != null) {
 63                 TreeNode pre = findMax(root.left);   // 找root前驱节点
 64                 root.val = pre.val;  // 前驱覆盖root
 65                 root.left = remove(root.left, pre.val);  // 删除pre
 66             } else {
 67                 TreeNode next = findMin(root.right);   // 找root后继节点
 68                 root.val = next.val;  // 后继覆盖root
 69                 root.right = remove(root.right, next.val);
 70             }
 71         } else if (x < root.val) {
 72             root.left = remove(root.left, x);
 73         } else {
 74             root.right = remove(root.right, x);
 75         }
 76         return root;
 77     }
 78 
 79     public void PreOrder(TreeNode root) { //先序遍历
 80         if (root == null)
 81             return;
 82         System.out.print(root.val + " ");
 83         PreOrder(root.left);
 84         PreOrder(root.right);
 85     }
 86 }
 87 
 88 class Test_demo {
 89     public static void main(String[] args) {
 90         String[] root = {"50", "17", "76", "9", "23", "54", null, null, "14", "19", null, null, "72"};
 91         int index = 0;
 92         TreeNode bt = createBTree(root, index);
 93         demo s = new demo();
 94 //        System.out.println(s.search(bt, 23));
 95 //        s.PreOrder(s.insert(bt, 25));
 96 //        s.PreOrder(s.create(new int[]{50, 17, 76, 9, 23, 54, 14, 19, 72}));
 97 //        System.out.println(s.findMax(bt).val);
 98 //        System.out.println(s.findMin(bt).val);
 99         s.PreOrder(s.remove(bt,50));
100     }
101 
102     public static TreeNode createBTree(String[] root, int index) {
103         TreeNode rootNode;
104         if (index >= root.length || root[index] == null) {
105             return null;
106         }
107         rootNode = new TreeNode(Integer.parseInt(root[index]));
108         rootNode.left = createBTree(root, 2 * index + 1);
109         rootNode.right = createBTree(root, 2 * index + 2);
110         return rootNode;
111     }
112 }

9、恢复二叉搜索树

问题：

给你二叉搜索树的根节点 root ，该树中的恰好两个节点的值被错误地交换。请在不改变其结构的情况下，恢复这棵树。

示例 1：

输入：root = [1,3,null,null,2]
输出：[3,1,null,null,2]
解释：3 不能是 1 的左孩子，因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
示例 2：

输入：root = [3,1,4,null,null,2]
输出：[2,1,4,null,null,3]
解释：2 不能在 3 的右子树中，因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。

 1 package LeetCode.test10_shu;
 2 
 3 /**
 4  * 思路： a=[1,2,3,4,5,6,7]
 5  * 如果交换两个不相邻的数字，例如2和6，原序列变成了a=[1,6,3,4,5,2,7]，那么显然序列中有两个位置不满足a(i)<a(i+1)
 6  * 在这个序列中体现为6>3，5>2，因此只要找到这两个位置，即可找到被错误交换的两个节点。
 7  * 如果交换两个相邻的数字，例如2和3，此时交换后的序列只有一个位置不满足a(i)<a(i+1)
 8  * 因此整个值序列中不满足条件的位置或者有两个，或者有一个。
 9  * eg:
10  * 3 2 1  (相邻)
11  * root = 3  pre=root=3   root=2   符合if条件 m1=3 m2=2  (m1==null)  自底而上
12  * pre=root=2
13  * root=1                          符合if条件 m1=3 m2=1  (m1!=null)
14  * 最后->   m1=3 m2=1
15  * 1 3 2 4  (不相邻)
16  * root=1  pre=root=1
17  * root=3  pre=root=3   root=4
18  * root=2                          符合if条件 m1=3 m2=2  (m1==null)
19  * pre=root=2
20  * root=4                          不符合if条件
21  * root=3                          最后->   m1=3 m2=2
22  */
23 public class ques_99_恢复二叉搜索树 {
24     private TreeNode mistake1 = null;
25     private TreeNode mistake2 = null;
26     private TreeNode pre = null;
27 
28     public void recoverTree(TreeNode root) {
29         InOrder(root);
30         if (mistake1 != null && mistake2 != null) {
31             int temp = mistake1.val;
32             mistake1.val = mistake2.val;
33             mistake2.val = temp;
34         }
35         testInOrder(root);
36     }
37 
38     private void InOrder(TreeNode root) {  // 中序遍历
39         if (root == null) {
40             return;
41         }
42         if (root.left != null) {
43             InOrder(root.left);
44         }
45         if (pre != null && pre.val > root.val) {
46             if (mistake1 == null) {
47                 mistake1 = pre;
48                 mistake2 = root;
49             } else {
50                 mistake2 = root;
51             }
52 //            System.out.println(mistake1.val);
53 //            System.out.println(mistake2.val);
54         }
55         pre = root;
56         if (root.right != null) {
57             InOrder(root.right);
58         }
59     }
60 
61     private void testInOrder(TreeNode root) {
62         if (root == null)
63             return;
64         testInOrder(root.left);
65         System.out.print(root.val + " ");
66         testInOrder(root.right);
67     }
68 }
69 
70 class Test_99 {
71     public static void main(String[] args) {
72         String[] root = {"1", "3", null, null, "2"};           // (321,3>2,2>1)
73 //        String[] root = {"3", "1", "4", null, null, "2"};    // (1324,3>2)
74         int index = 0;
75         TreeNode bt = createBTree(root, index);
76         ques_99_恢复二叉搜索树 s = new ques_99_恢复二叉搜索树();
77         s.recoverTree(bt);
78     }
79 
80     public static TreeNode createBTree(String[] root, int index) {
81         TreeNode rootNode;
82         if (index >= root.length || root[index] == null) {
83             return null;
84         }
85         rootNode = new TreeNode(Integer.parseInt(root[index]));
86         rootNode.left = createBTree(root, 2 * index + 1);
87         rootNode.right = createBTree(root, 2 * index + 2);
88         return rootNode;
89     }
90 }

View Code

10、修剪二叉搜索树

问题：

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。

修剪树不应该改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。可以证明，存在唯一的答案。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]
示例 2：

输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

 1 package LeetCode.test10_shu;
 2 
 3 /**
 4  * 思路：
 5  * 当root.val > R，那么修剪后的二叉树必定出现在节点的左边。
 6  * 当root.val < L，那么修剪后的二叉树出现在节点的右边。
 7  * 否则，将会修剪树的两边。
 8  */
 9 public class ques_669_修剪二叉搜索树 {
10     public TreeNode trimBST(TreeNode root, int low, int high) {
11         if (root == null) {
12             return root;
13         }
14         if (root.val > high) {
15 //            root = root.left;
16 //            root = trimBST(root, low, high);
17             return trimBST(root.left, low, high);
18         }
19         if (root.val < low) {  // 0符合条件
20 //            root = root.right;
21 //            root = trimBST(root, low, high);
22             return trimBST(root.right, low, high);
23         }
24         root.left = trimBST(root.left, low, high);  // 修剪左子树（0） ->  root.left = null
25         root.right = trimBST(root.right, low, high); // 修剪右子树（2）->  root.right = 2
26         return root;
27     }
28 }
29 
30 class Test_669 {
31     public static void main(String[] args) {
32         String[] root = {"1", "0", "2"};
33         int index = 0;
34         int low = 1, high = 2;
35         TreeNode bt = createBTree(root, index);
36         ques_669_修剪二叉搜索树 s = new ques_669_修剪二叉搜索树();
37         s.trimBST(bt, low, high);
38     }
39 
40     public static TreeNode createBTree(String[] root, int index) {
41         TreeNode rootNode;
42         if (index >= root.length || root[index] == null) {
43             return null;
44         }
45         rootNode = new TreeNode(Integer.parseInt(root[index]));
46         rootNode.left = createBTree(root, 2 * index + 1);
47         rootNode.right = createBTree(root, 2 * index + 2);
48         return rootNode;
49     }
50 }

View Code

补：

例1

问题：二叉搜索树与双向链表

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。如下图所示

注意:

1.要求不能创建任何新的结点，只能调整树中结点指针的指向。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode，有左右指针，其实可以看成一个双向链表的数据结构

4.你不用输出双向链表，程序会根据你的返回值自动打印输出

输入描述：二叉树的根节点

返回值描述：双向链表的其中一个头节点。

示例 1：

输入：

{10,6,14,4,8,12,16}

返回值：

From left to right are:4,6,8,10,12,14,16;From right to left are:16,14,12,10,8,6,4;

示例 2：

输入：

{5,4,#,3,#,2,#,1}

返回值：

From left to right are:1,2,3,4,5;From right to left are:5,4,3,2,1;

 1 import java.util.*;
 2 
 3 public class Solution {
 4     TreeNode head = null;
 5     TreeNode preNode = null;
 6         
 7     public TreeNode Convert(TreeNode pRootOfTree) {
 8         if(pRootOfTree == null){
 9             return null;
10         }
11         Convert(pRootOfTree.left);
12         if(preNode == null){
13             head = pRootOfTree;
14             preNode = pRootOfTree;
15         }else{
16             preNode.right = pRootOfTree;
17             pRootOfTree.left = preNode;
18             preNode = pRootOfTree;
19         }
20         Convert(pRootOfTree.right);
21         return head;
22     }
23 }

View Code

例2

问题：判断是不是二叉搜索树

给定一个二叉树根节点，请你判断这棵树是不是二叉搜索树。

二叉搜索树满足每个节点的左子树上的所有节点均严格小于当前节点且右子树上的所有节点均严格大于当前节点。

示例 1：

输入：{1,2,3}

返回值：false

示例 2：

输入：{2,1,3}

返回值：true

 1 import java.util.*;
 2 
 3 public class Solution {
 4     int pre = Integer.MIN_VALUE;
 5 
 6     public boolean isValidBST (TreeNode root) {
 7         // write code here
 8         if(root==null){
 9             return true;
10         }
11         //先遍历左子树
12         if(isValidBST(root.left)==false){
13             return false;
14         }
15         if(root.val < pre){
16             return false;
17         }
18         pre = root.val;    
19         return isValidBST(root.right);
20     }
21 }

View Code

例3

问题：二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

1.对于该题的最近的公共祖先定义:对于有根树T的两个节点p、q，最近公共祖先LCA(T,p,q)表示一个节点x，满足x是p和q的祖先且x的深度尽可能大。在这里，一个节点也可以是它自己的祖先.

2.二叉搜索树是若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值

3.所有节点的值都是唯一的。

4.p、q 为不同节点且均存在于给定的二叉搜索树中。

数据范围:3<=节点总数<=10000　　0<=节点值<=10000

示例 1：

输入：{7,1,12,0,4,11,14,#,#,3,5},1,12

返回值：7

示例 2：

输入：{7,1,12,0,4,11,14,#,#,3,5},12,11

返回值：12

 1 import java.util.*;
 2 
 3 public class Solution {
 4     public int lowestCommonAncestor (TreeNode root, int p, int q) {
 5         // write code here
 6         ArrayList<Integer> pathP = getPath(root,p);
 7         ArrayList<Integer> pathQ = getPath(root,q);
 8         int res = 0;
 9         for(int i = 0; i < pathP.size() && i < pathQ.size(); i++){
10             int x = pathP.get(i);
11             int y = pathQ.get(i);
12             if(x == y){
13                 res = pathP.get(i); // 覆盖
14             }else{
15                 break;
16             }
17         }
18         return res;
19         // return helper(root, p, q).val;
20     }
21     
22     public ArrayList<Integer> getPath(TreeNode root, int target){
23         ArrayList<Integer> path = new ArrayList<>();
24         TreeNode node = root;
25         while(node.val != target){
26             path.add(node.val);
27             if(node.val > target){
28                 node = node.left;
29             }else{
30                 node = node.right;
31             }
32         } 
33         path.add(node.val);
34         return path;
35     }
36     
37     public TreeNode helper(TreeNode root, int o1, int o2){
38         if(root == null || root.val == o1 || root.val == o2){
39             return root;
40         }
41         TreeNode left = helper(root.left,o1,o2);
42         TreeNode right = helper(root.right,o1,o2);
43         if(left == null){
44             return right;
45         }
46         if(right == null){
47             return left;
48         }
49         return root;
50     }
51 }

View Code

例4

问题：在二叉树中找到两个节点的最近公共祖先

给定一棵二叉树(保证非空)以及这棵树上的两个节点对应的val值 o1 和 o2，请找到 o1 和 o2 的最近公共祖先节点。

要求：时间复杂度

注：本题保证二叉树中每个节点的val值均不相同。

示例 1：

输入：{3,5,1,6,2,0,8,#,#,7,4},5,1

返回值：3

示例 2：

输入：{3,5,1,6,2,0,8,#,#,7,4},2,7

返回值：2

 1 import java.util.*;
 2 
 3 public class Solution {
 4     public int lowestCommonAncestor (TreeNode root, int o1, int o2) {
 5         // 非递归写法
 6         // return helper1(root, o1, o2);
 7         
 8         // 递归写法
 9         return helper2(root, o1, o2).val;
10     }
11     
12     public int helper1(TreeNode root, int o1, int o2){
13         Map<Integer,Integer> parents = new HashMap<>();
14         Queue<TreeNode> queue = new LinkedList<>();
15         parents.put(root.val,Integer.MIN_VALUE);
16         queue.add(root);
17         
18         while(!parents.containsKey(o1)||!parents.containsKey(o2)){
19             TreeNode node = queue.poll();
20             if(node.left!=null){
21                 parents.put(node.left.val,node.val);
22                 queue.add(node.left);
23             }
24             if(node.right!=null){
25                 parents.put(node.right.val,node.val);
26                 queue.add(node.right);
27             }
28         }
29         List<Integer> path = new ArrayList<>();
30         while(parents.containsKey(o1)){
31             path.add(o1);
32             o1 = parents.get(o1);
33         }
34         
35         while(!path.contains(o2)){
36             o2 = parents.get(o2);
37         }
38         return o2;
39     }
40     
41     public TreeNode helper2(TreeNode root, int o1, int o2){
42         if(root == null || root.val == o1 || root.val == o2){
43             return root;
44         }
45         TreeNode left = helper2(root.left,o1,o2);
46         TreeNode right = helper2(root.right,o1,o2);
47         if(left == null){
48             return right;
49         }
50         if(right == null){
51             return left;
52         }
53         return root;
54     }
55 }

View Code

五、字典树

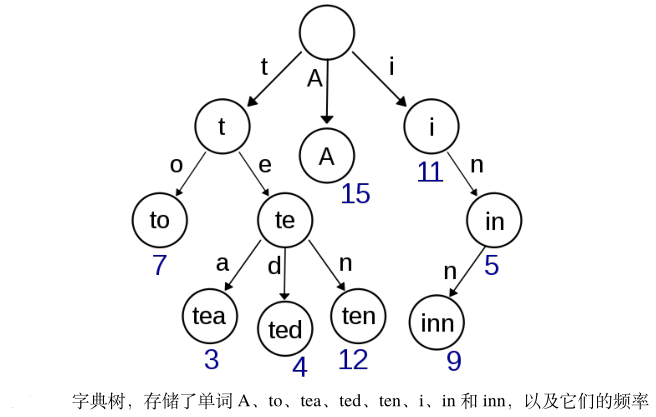
11、实现Trie

问题：

Trie（发音类似 "try"）或者说前缀树是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：

输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]

解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True

 1 package LeetCode.test10_shu;
 2 
 3 class TrieNode{
 4 //    TrieNode[] children = new TrieNode[26];
 5     TrieNode[] children;
 6     boolean isEnd;
 7 
 8     public TrieNode() {
 9 //        for (int i = 0; i < 26; i++) {
10 //            children[i] = null;
11 //            isEnd = false;
12 //        }
13         this.children = new TrieNode[26];
14         this.isEnd = false;
15     }
16 }
17 
18 public class ques_208_实现Trie {
19     private TrieNode root;
20 
21     public ques_208_实现Trie() {
22         root = new TrieNode();
23 //        root.isEnd = false;
24     }
25 
26     public void insert(String word) {
27         TrieNode temp = root;
28         for (int i = 0; i < word.length(); i++) {
29             char c = word.charAt(i);
30             int index = c - 'a';
31             if (temp.children[index] == null) {
32                 temp.children[index] = new TrieNode();
33             }
34             temp = temp.children[index];
35         }
36         temp.isEnd = true;
37     }
38 
39     public boolean search(String word) {
40         TrieNode temp = root;
41         for (int i = 0; i < word.length(); i++) {
42             char c = word.charAt(i);
43             int index = c - 'a';
44             if (temp.children[index] == null) {
45                 return false;
46             }
47             temp = temp.children[index];
48         }
49         return temp.isEnd;
50     }
51 
52     public boolean startsWith(String prefix) {
53         TrieNode temp = root;
54         for (int i = 0; i < prefix.length(); i++) {
55             char c = prefix.charAt(i);
56             int index = c - 'a';
57             if (temp.children[index] == null) {
58                 return false;
59             }
60             temp = temp.children[index];
61         }
62         return true;
63     }
64 }
65 
66 class Test_ques_208_实现Trie {
67     public static void main(String[] args) {
68         ques_208_实现Trie trie = new ques_208_实现Trie();
69 //        trie.insert("apple");
70 //        trie.search("apple");
71 //        trie.search("app");
72 //        trie.startsWith("app");
73 //        trie.insert("app");
74 //        trie.search("app");
75     }
76 }

View Code

练习

基础难度

226. Invert Binary Tree (Easy)
巧用递归，你可以在五行内完成这道题。
617. Merge Two Binary Trees (Easy)
同样的，利用递归可以轻松搞定。
572. Subtree of Another Tree (Easy)
子树是对称树的姊妹题，写法也十分类似。
404. Sum of Left Leaves (Easy)
怎么判断一个节点是不是左节点呢？一种可行的方法是，在辅函数里多传一个参数，表示当
前节点是不是父节点的左节点。
513. Find Bottom Left Tree Value (Easy)
最左下角的节点满足什么条件？针对这种条件，我们该如何找到它？
538. Convert BST to Greater Tree (Easy)
尝试利用某种遍历方式来解决此题，每个节点只需遍历一次。
235. Lowest Common Ancestor of a Binary Search Tree (Easy)
利用 BST 的独特性质，这道题可以很轻松完成。
530. Minimum Absolute Difference in BST (Easy)
还记得我们所说的，对于 BST 应该利用哪种遍历吗？

进阶难度
889. Construct Binary Tree from Preorder and Postorder Traversal (Medium)
给定任意两种遍历结果，我们都可以重建树的结构。
106. Construct Binary Tree from Inorder and Postorder Traversal (Medium)
给定任意两种遍历结果，我们都可以重建树的结构。
94. Binary Tree Inorder Traversal (Medium)
因为前中序后遍历是用递归实现的，而递归的底层实现是栈操作，因此我们总能用栈实现。
145. Binary Tree Postorder Traversal (Medium)
因为前中序后遍历是用递归实现的，而递归的底层实现是栈操作，因此我们总能用栈实现。
236. Lowest Common Ancestor of a Binary Tree (Medium)
现在不是 BST，而是普通的二叉树了，该怎么办？
109. Convert Sorted List to Binary Search Tree (Medium)
把排好序的链表变成 BST。为了使得 BST 尽量平衡，我们需要寻找链表的中点。
897. Increasing Order Search Tree (Easy)
把 BST 压成一个链表，务必考虑清楚指针操作的顺序，否则可能会出现环路。
653. Two Sum IV - Input is a BST (Easy)
啊哈，这道题可能会把你骗到。
450. Delete Node in a BST (Medium)
当寻找到待删节点时，你可以分情况考虑——当前节点是叶节点、只有一个子节点和有两个
子节点。建议同时回收内存。

posted on 2022-03-17 16:43 晨曦生辉耀匕尖阅读(49) 评论(0) 编辑收藏举报

刷新页面返回顶部

第十章：树

公告