一、动态规划（背包问题）
问题1：Bone Collector（二维）
Many years ago , in Teddy’s hometown there was a man who was called “Bone Collector”. This man like to collect varies of bones , such as dog’s , cow’s , also he went to the grave …
The bone collector had a big bag with a volume of V ,and along his trip of collecting there are a lot of bones , obviously , different bone has different value and different volume, now given the each bone’s value along his trip , can you calculate out the maximum of the total value the bone collector can get ?
Input：The first line contain a integer T , the number of cases.
Followed by T cases , each case three lines , the first line contain two integer N , V, (N <= 1000 , V <= 1000 )representing the number of bones and the volume of his bag. And the second line contain N integers representing the value of each bone. The third line contain N integers representing the volume of each bone.
Output：One integer per line representing the maximum of the total value (this number will be less than 2 31).
Sample Input
1 5 10 1 2 3 4 5 5 4 3 2 1
Sample Output
14
代码：
#include <cstdio> #include <iostream> #include <cstring> using namespace std; struct BONE{ int value; int weight; }num[110]; int DP(); int n,v; int dp[110][110]; int main(){ int t; cin>>t; while(t--){ cin>>n>>v; for(int i=1;i<=n;i++){ cin>>num[i].value; } for(int i=1;i<=n;i++){ cin>>num[i].weight; } cout<<DP()<<endl; } return 0; } int DP(){ memset(dp,0,sizeof(dp)); for(int i=1;i<=n;i++){ for(int j=0;j<=v;j++){ if(num[i].weight>j){ dp[i][j] = dp[i-1][j]; }else{ dp[i][j] = max(dp[i-1][j],dp[i-1][j-num[i].weight]+num[i].value); } } } return dp[n][v]; }
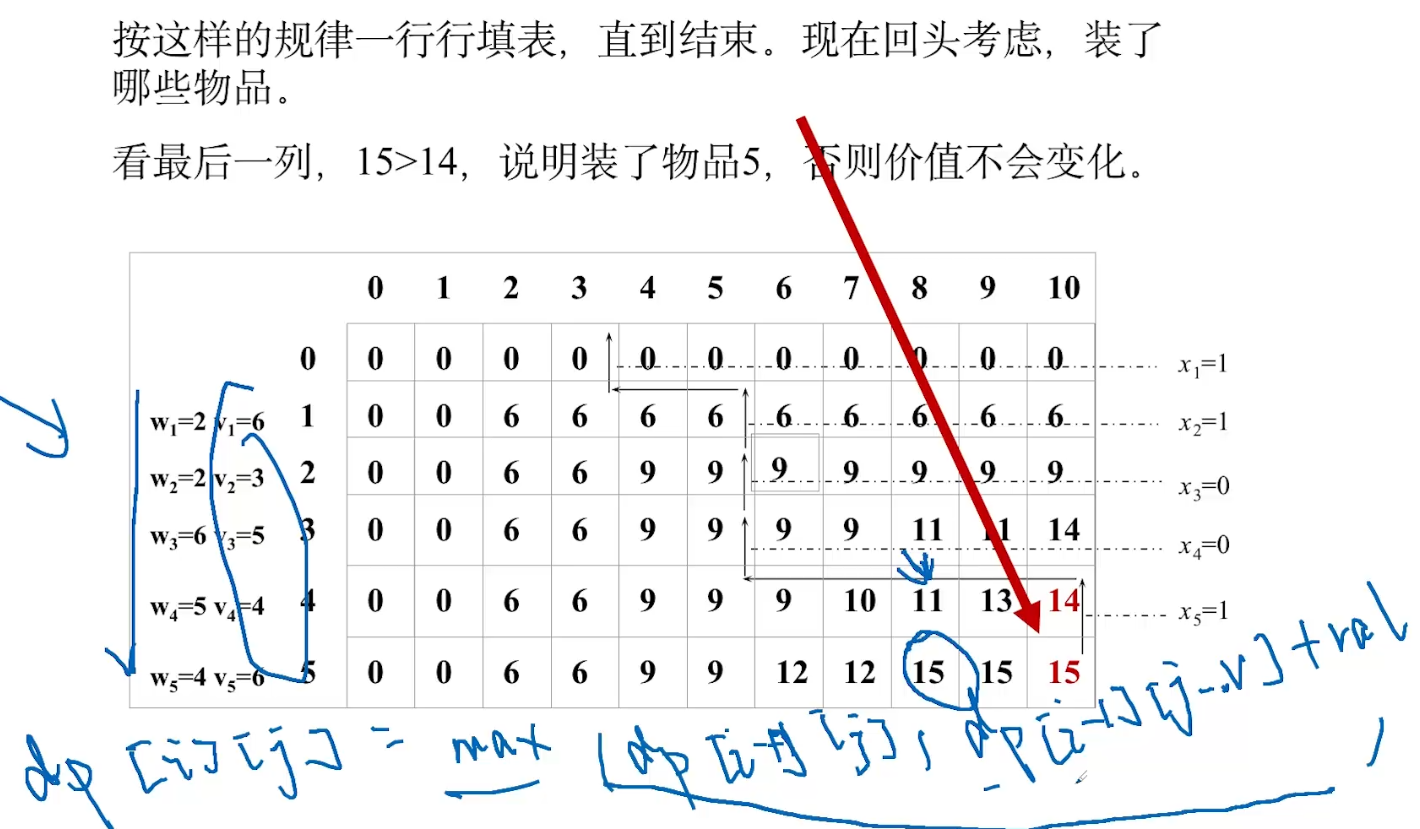
问题2：（一维）
题目描述
输入
数组中的元素
输出
降序输出两个子数组的元素和
样例输入 Copy
10 20 30 10 10
10 20 abc 10 10
样例输出 Copy
40 40
ERROR
代码：
#include<iostream> #include<algorithm> #include<cstring> #include<map> #include<cmath> using namespace std; int a[100],dp[100],num[100],p=1; int sum=0; int main(){ memset(a,0,sizeof(a)); memset(dp,0,sizeof(dp)); string s; while(cin>>s){ int len = (int)s.size(); int flag = 0; for(int i=0;i<len;i++){ if(s[i]>='0'&&s[i]<='9'){ a[p] = a[p]*10 +(s[i]-'0'); }else{ flag = 1; } } if(flag==1){ cout<<"ERROR"<<endl; } p++; } for(int i=1;i<p;i++){ cin>>a[i]; sum+=a[i]; } for(int i=1;i<p;i++){ for(int V=sum/2;V>=a[i];V--){ dp[V] = max(dp[V],dp[V-a[i]]+a[i]); } } if(dp[sum/2]>sum-dp[sum/2]){ cout<<dp[sum/2]<<" "<<sum-dp[sum/2]<<endl; }else{ cout<<sum-dp[sum/2]<<" "<<dp[sum/2]<<endl; } return 0; }
二、最长公共子序列
问题：Common Subsequence
A subsequence of a given sequence is the given sequence with some elements (possible none) left out. Given a sequence X = <x1, x2, ..., xm> another sequence Z = <z1, z2, ..., zk> is a subsequence of X if there exists a strictly increasing sequence <i1, i2, ..., ik> of indices of X such that for all j = 1,2,...,k, xij = zj. For example, Z = <a, b, f, c> is a subsequence of X = <a, b, c, f, b, c> with index sequence <1, 2, 4, 6>. Given two sequences X and Y the problem is to find the length of the maximum-length common subsequence of X and Y.
The program input is from a text file. Each data set in the file contains two strings representing the given sequences. The sequences are separated by any number of white spaces. The input data are correct. For each set of data the program prints on the standard output the length of the maximum-length common subsequence from the beginning of a separate line.
Input：
abcfbc abfcab programming contest abcd mnp
Output：
4 2 0
Sample Input：
abcfbc abfcab programming contest abcd mnp
Sample Output：
4 2 0
代码：
#include <cstdio> #include <iostream> #include <cstring> using namespace std; int dp[100][100]; int main(){ string s1,s2; while(cin>>s1>>s2){ memset(dp,0,sizeof(dp)); for(int i=1;i<=(int)s1.size();i++){ for(int j=1;j<=(int)s2.size();j++){ if(s1[i-1]==s2[j-1]){ dp[i][j] = dp[i-1][j-1]+1; }else{ dp[i][j] = max(dp[i-1][j],dp[i][j-1]); } } } cout<<dp[s1.size()][s2.size()]<<endl; } return 0; }
三、最长递增子序列
问题1：最少拦截系统
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统.但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能超过前一发的高度.某天,雷达捕捉到敌国的导弹来袭.由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹.
怎么办呢?多搞几套系统呗!你说说倒蛮容易,成本呢?成本是个大问题啊.所以俺就到这里来求救了,请帮助计算一下最少需要多少套拦截系统.
Input：输入若干组数据.每组数据包括:导弹总个数(正整数),导弹依此飞来的高度(雷达给出的高度数据是不大于30000的正整数,用空格分隔)
Output：对应每组数据输出拦截所有导弹最少要配备多少套这种导弹拦截系统.
Sample Input
8 389 207 155 300 299 170 158 65
Sample Output
2
代码：
#include <cstdio> #include <iostream> #include <cstring> using namespace std; int main(){ int n,temp[100],dp[100]; cin>>n; for(int i=1;i<=n;i++){ cin>>temp[i]; } int ans = -1; for(int i=1;i<=n;i++){ dp[i]=1; for(int j=0;j<i;j++){ if(temp[i]>temp[j]&&dp[j]+1>dp[i]){ dp[i] = dp[j]+1; } } ans = max(ans,dp[i]); } cout<<ans<<endl; return 0; }
问题2：合唱队形
题目描述
N位同学站成一排，音乐老师要请其中的(N-K)位同学出列，使得剩下的K位同学不交换位置就能排成合唱队形。
合唱队形是指这样的一种队形：设K位同学从左到右依次编号为1, 2, …, K，他们的身高分别为T1, T2, …, TK，
则他们的身高满足T1 < T2 < … < Ti , Ti > Ti+1 > … > TK (1 <= i <= K)。
你的任务是，已知所有N位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。
输入
输入的第一行是一个整数N（2 <= N <= 100），表示同学的总数。
第一行有n个整数，用空格分隔，第i个整数Ti（130 <= Ti <= 230）是第i位同学的身高（厘米）。
输出
可能包括多组测试数据，对于每组数据，
输出包括一行，这一行只包含一个整数，就是最少需要几位同学出列。
样例输入 Copy
3
174 208 219
6
145 206 193 171 187 167
0
样例输出 Copy
0
1
代码：
#include <cstdio> #include <iostream> #include <cstring> #include <algorithm> #include <cmath> using namespace std; int main(){ int a[110],dp1[110],dp2[110],ans[110]; int n; while(cin>>n){ if(n==0){ break; } for(int i=0;i<n;i++){ cin>>a[i]; } for(int i=0;i<n;i++){ dp1[i] = 1; for(int j=0;j<i;j++){ if(a[j]<a[i]&&dp1[j]+1>dp1[i]){ dp1[i]=dp1[j]+1; } } } int Max = 0; for(int i=n-1;i>=0;i--){ dp2[i] = 1; for(int j=n-1;j>i;j--){ if(a[j]<a[i]&&dp2[j]+1>dp2[i]){ dp2[i]=dp2[j]+1; } } ans[i] = dp1[i]+dp2[i]-1; Max = max(Max,ans[i]); } cout<<n-Max<<endl; } return 0; }
四、最大连续子序列和（同二维结合起来）
题目描述：
已知矩阵的大小定义为矩阵中所有元素的和。给定一个矩阵，你的任务是找到最大的非空(大小至少是1 * 1)子矩阵。
比如，如下4 * 4的矩阵
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
的最大子矩阵是
9 2
-4 1
-1 8
这个子矩阵的大小是15。
输入：
输入是一个N * N的矩阵。输入的第一行给出N (0 < N <= 100)。
再后面的若干行中，依次（首先从左到右给出第一行的N个整数，再从左到右给出第二行的N个整数……）给出矩阵中的N2个整数，整数之间由空白字符分隔（空格或者空行）。
已知矩阵中整数的范围都在[-127, 127]。
输出：
测试数据可能有多组，对于每组测试数据，输出最大子矩阵的大小。
样例输入：
1
27
3
-40 29 -16
38 18 22
24 -35 5
样例输出：
27
78
分析：
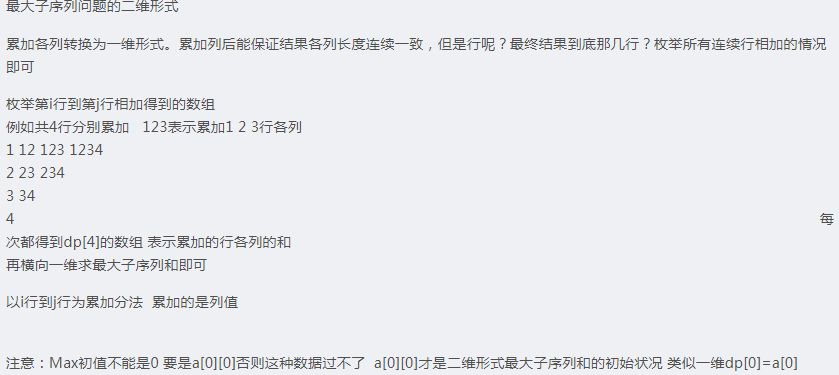
代码：
#include<iostream> #include<algorithm> #include<cstring> #include<map> #include<cmath> using namespace std; int a[100][100],dp[100]; int max_sub(int t[]); int n; int MAX_1; int main(){ while(cin>>n){ for(int i=0;i<n;i++){ for(int j=0;j<n;j++){ cin>>a[i][j]; } } MAX_1 = a[0][0]; for(int i=0;i<n;i++){ memset(dp,0,sizeof(dp)); for(int j=i;j<n;j++){ for(int k=0;k<n;k++){ dp[k]+=a[j][k]; } int MAX_2 = max_sub(dp); if(MAX_2>MAX_1){ MAX_1 = MAX_2; } } } cout<<MAX_1<<endl; } return 0; } int max_sub(int a[]){ int ans = -0x3f3f3f3f,dp[100]; dp[0] = a[0]; for(int i=1;i<n;i++){ dp[i] = max(a[i],dp[i-1]+a[i]); } for(int i=0;i<n;i++){ ans = max(ans,dp[i]); } return ans; }
