haskell学习笔记
Haskell学习笔记
零零碎碎,按照《Haskell趣学指南》顺序学习,未必有很明确的体系,也不会把所有的内容都记录。我会记录下我觉得有趣、有用、有意义、有不同的点。
这样的记录方式想必是很难复习和整理的,如果有闲了再整理吧。就供有缘人和有缘的未来我通过查找与这些再次相遇。
预备知识
函数
优先级
Haskell函数调用不使用括号将参数包围。仅用空格将函数名和参数隔开。因此函数调用拥有最高的优先级。例如:
succ 9 * 10
是先取9的后继,再与10相乘。
中缀函数 SP
适用于有两个参数的函数,比如:
div 91 10
91 `div` 10
以上两种写法等价。即用反引号将函数名包围,使用中缀函数的形式调用。
中缀写法在定义函数时候也可以这么写。
函数声明与定义
先写函数名,后跟由空格分隔的参数表。之后用等号=分隔,之后定义函数的行为。函数体由=和换行等内容来区分,是很不同的一件事;
函数定义没有先后顺序,因此后面定义的函数前面也可以用。
函数名称中的单引号',大写与零参数
通常在函数名字最后加个‘表示这是个函数的严格求值版本。
函数名称首字母不能大写。
如果没有参数,这个函数被称为定义或者名字。函数定义后不能修改内容。
$
$符号可以用来代替括号,当给一个函数传的参数里面,有的参数是通过一个复杂表达式生成的,这时候除了用括号包围,也可以用 $分隔
take 1 $ filter even [1..10]
take 1 (filter even [1..10])
条件判断if
看这个例子,说明了基本语法:
doubleX x = if x > 100
then x
else x*2
else部分不可省略,这很特殊。究其原因,在于Haskell中,程序是一系列函数的集合。if也不例外,本质上仍然是个函数,或者说是一个必然返回结果的表达式(expression)。而不是一个语句(statement)。
列表
列表要求元素类型相同。
列表操作
- 列表拼接使用操作符 ++
- 字符串可以使用列表的所有函数
- 操作对象是两个列表
- 太长的会很慢
- 在列表头部加入一个元素使用:
- 操作对象是一个元素和一个列表
[1,2,3] 是1:2:3:[]的语法糖
- 列表索引使用操作符!!
- 列表也可以比较,依次比较元素
- 其他操作
- head 取第一个元素
- tail 取除了第一个元素的列表
- last 取最后一个元素
- init 取除了最后一个元素的列表
- length 返回长度
- null 检查空否
- reverse 翻转
- take 参数有一个数字和一个列表,取指定的前几个元素
- drop 删除前几个元素
- maximum minimum 取最小元素
- sum求和 product求积
- elem 检查是否包含,可以用中缀
range与无限列表
给出起始和终止,再给出步长,可以生成要求的列表。用 .. 写到列表里面。

若不标明上限,会得到一个无限列表。可以配合take实现一些效果。

由于有惰性求值,无限列表不会被真正求出来。
- cycle函数接受一个列表作为参数,返回一个无限列表
- repeat 接受一个值作为函数,返回一个无限列表
- replicate 接受一个个数,一个元素,返回确定长度的重复值列表
range里用浮点数不太好,由于精度有限。
列表推导式
先看例子,这与数学中集合的表示方式有点像:
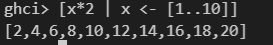
竖线前是输出,<-表示x取后面这个列表中的所有值。
当然可以在列表推导式中再添加谓词,用逗号分隔。这种操作也称为过滤filter:

谓词可以有多个,也可以从多个列表中取元素,甚至可以嵌套。
初步来看,python中的列表推导式更好理解一些。
元组
元素类型不限制,但是长度必须确定。具体位置上类型不同的元组是不同类的。不能有单元素的元组。可以比较。
使用
-
fst函数与snd函数---只能用于处理二元组,取元组中项。
-
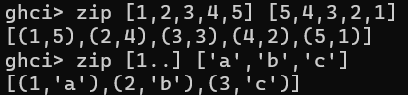
zip函数,将两个列表中元素配对,生成一组二元组的列表,看如下的例子:
![image-20220308172848095]()
对于长列表,在短列表用完之后就会停止。
运用示例
要求输出满足:
- 三边长度均为整数
- 三遍长度均小于10
- 周长=24
的直角三角形,用元组表示,ghci代码如下。
ghci> let triangles = [ (a,b,c) | c<-[1..10], a<-[1..c], b<-[1..a], a^2+b^2==c^2, a+b+c==24]
ghci> triangles
[(8,6,10)]
类型系统
Haskell支持类型推导,编译时会确定表达式类型。一切皆有类型。
显式类型声明
-
用
:t expression来检查表达式的类型 -
明确的类型的首字母必须大写
-
::的意思是“类型为”,比如4 == 5 :: Bool -
函数也有类型,编写函数前给函数增加一个显式类型声明
-
addThree :: Int -> Int -> Int -> Int addThree x y z =x+y+z -
参数与返回值通过->分隔,最后一项是返回值的类型
-
类型变量
先看这个例子:
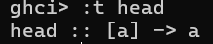
a可以指代任意一个类型。说白了其实就是泛型,像C++里的模板函数。
类型变量没有首字母大写的限制,一般用单个的小写字母代替即可,多个也行。
类型类 typeclass
类型类是定义行为的接口。如果一个类型是一个类型类的实例,则他必须实现该类型类描述的行为。
类型类是一组函数的集合。某类型实现为某类型类的实例,就需要为该类型提供这些函数的相应实现。(其实就是接口啊啊)
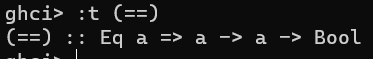
- 运算符也是函数。如果一个函数名字全不是字母,则默认为中缀函数。要检查其类型或者用前缀调用,需要括号括起来
- =>符号是类型约束的意思。在这里表示“限制a类型是Eq类的实例”
- Eq这里类型类提供了判断相等的接口。可比较相等性的类型必属于Eq类。
除了Eq类型类,还有一些:
-
Eq要求实现==和/=两个函数
-
Ord要求实现< > <= >=
- compare函数取两个Ord中相同类型的值作为参数,返回一个Ordering类型的值。包括GT,LT和EQ三个值。
-
Show要求该类型实例可以转为字符串,toString
-
Read要求该类型有字符串转为类型类,是Show的相反
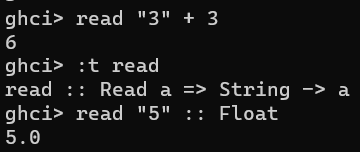
- 这两个类的签名中用的是类型变量,如果有进一步运算当然可以帮助确定类型,如果没有的话需要加类型注解。
![image-20220308181756753]()
- 提供最少的信息就行,如下他一样能判断。
![image-20220308181955459]()
-
Enum的实例类型是有连续顺序的,值可枚举;每个值都有相应的类型前驱和后继,主要用于在区间里使用。
- (), Bool, Char, Ordering, Int, Integer, Float, Double
函数-2
模式匹配
先看一个例子:
lucky :: Int -> String
lucky 7 = "lucky number"
lucky x = "Not lucky enough"
在这个函数中,会将传入的参数按从上至下的顺序检查模式,有匹配则调用对应的函数体。
最后一个模式x匹配一切数值并绑定为x。这被称为万能模式,有点类似switch case中的default。这样可以避免写出太大的if-then-else语句。如果没有万能模式会崩溃报错,因此一定要写。
模式匹配和用在一切赋值结构中。
使用模式匹配可以写出递归函数,如下面的阶乘:
fact :: Int -> Int
fact 0 = 1
fact n = n * fact (n-1)
元组
如下两种函数写法中,使用了模式匹配的可读性更好,还为元组中的项赋予了名字。同时本身就是一个万能匹配。
addV :: (Double, Double) -> (Double, Double) -> (Double, Double)
addV a b = (fst a + fst b, snd a+snd b)
addV (x1,y1) (x2,y2) = (x1+x2,y1+y2)
列表
列表推导式中也可以用模式匹配。
普通的列表,可以用 []来匹配空列表,用:和[]来匹配非空列表。
as模式
按模式把一个值分割成多个项,同时保留对整体的引用。
fstletter all@(x:xs) = "the fst letter of "++ all ++ " is "++[x]
case表达式
模式匹配其实是case表达式的语法糖。语法结构如下
case expression of pattern1 -> result
pattern2 -> result
....
describeList :: [a] -> String
describeList ls = "this is " ++ case ls of [] -> "empty"
[x] -> "singleton"
xs -> "longer"
case模式匹配可以用在任何地方,随便插入到表达式的什么地方都可以。
哨兵guard
也是有点像ifelse,但是能很好的和模式匹配契合也可读性更好。示例如下:
bmiTell :: Double -> String
bmiTell bmi
| bmi <= 18.5 = "underweight"
| bmi <= 25.0 = "normal"
| bmi <= 30.0 = "fat"
| otherwise = "whale"
哨兵在竖线的右边,即为一个布尔表达式,计算为True则选择。
最后一个是otherwise,捕获一切条件;如果没有otherwise,那就进入函数的下一个模式。
where
where关键字用于保存计算的中间结果,避免重复计算。
比如对上面的bmi函数进行功能改变,成为一个输入身高和体重的函数。
bmiTell :: Double -> Double -> String
bmiTell weight height
| bmi <= 18.5 = "underweight"
| bmi <= 25.0 = "normal"
| bmi <= 30.0 = "fat"
| otherwise = "whale"
where bmi = weight / height ^ 2
where关键字跟在哨兵后面,在这里面可以随意定义名字和函数,对于哨兵都是可见的。
注意where中变量的定义都必须对齐到一列。
where的作用域
- 只对本函数可见。
- 进一步的,只对本函数的当前模式可见。
where的模式匹配
比如这个函数:
initials :: String -> String -> String
initials firstname lastname = [f] ++ ". " ++ [l] ++"."
where (f:_)=firstname
(l:_)=lastname
当然这样些有些冗长了,在参数上直接模式匹配就好。
where中定义函数
复杂一些,定义的函数也要有参数,并且该函数会被函数调用。
let
let可以在任何位置定义局部变量,且对其他哨兵不可见。其格式为: let <bindings> in <expressions>.在bindings中的名字仅在in中可见。
看上去与where的差距就是先写表达式还是先写名字绑定。实际上,let语句是一个表达式,也就是拥有返回值的。因此let语句可以放在代码的任意位置。先声明、后使用的思路,符合程序员思维。
-
可以用于在局部作用域中定义函数
-
多个名字绑定时,需要用分号隔开
-
用于从元组中取值
![]()
但其实let语法在写的时候可能会因为in的含义而导致出现理解错误,理解为先声明再使用就好一些。
- 列表推导式
- 将let表达式放在谓词的地方,与其他用逗号隔开
- 不带in了,只起到绑定变量的作用,也不起到谓词的过滤作用
- 绑定的变量可以用在输出部分(|前)和其他谓词中
- 生成器(<-的部分)中没法用,这涉及到定义的先后顺序。
let通常作用域很短,还是where更流行。
递归
Haskell中的递归非常不同。在命令式语言中,程序员要告诉编译器如何计算how;在函数式语言里,我们要声明是什么what的问题。求解步骤不再重要,而是定义问题与解的描述。
一些库函数的实现不再抄一遍了。来给出Haskell至今为止让我最震惊的地方:非常优雅的实现快速排序。
qSort :: (Ord a) => [a] -> [a]
qSort [] = []
qSort (x:xs) =
let smallerORequal = [a | a <- xs , a <= x]
larger = [a | a <- xs, a > x]
in qSort smallerORequal ++ [x] ++ qSort larger
太优雅了。以往的命令式语言里实现快排也许有简短的,但没有这么简明易懂的。
高阶函数
函数的参数也是函数。能够起到很好的解决问题、简化代码的效果。
柯里函数
本质上,Haskell的函数都是只有一个参数的。多参数的函数实际上都是每次只取一个参数,并返回一个一元函数来取下一个参数。
比如说,以下两种调用是等价的:
max 4 5
(max 4) 5
再来看函数类型签名中的 ->号。这个箭头意味着将左侧视作参数类型,将右侧视作返回值。
对于 a -> (a -> a),含义其实就是:一个函数取类型为a的值做参数,返回值是一个函数;返回的函数取类型为a的值做参数,返回类型为a。
这样做的好处是,如果我们使用“部分参数”来调用函数,就可以得到一个部分应用函数。这个部分应用函数的参数数量即是之前少传入的参数数量。这使得我们能很方便的构造新函数。
cmpWith100 :: Int -> Ordering
cmpWith100 x = compare 100 x
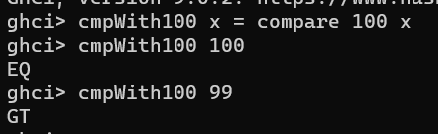
效果不错,可以偷懒少输入一个参数了。(更重要的是方便的构建了新函数!)
截断
通过截断实现对中缀函数的部分应用。实现过程是:将一个参数放在中缀函数的一侧,外面用括号包围,就实现对这个中缀函数的截断并得到了一个一元函数, 其参数为中缀函数剩余的参数。
divBy10 :: (Floating a) => a -> a
divBy10 = (/10)
-- / 即除号除法本身就是一个中缀函数,不用`包围也是中缀。
isUpperletter :: Char -> Bool
isUpperletter = (`elem` ['A'..'Z'])
-- 这里就需要用反引号了
注意如果想要用-号(减号与负号)时,不能这么写,要用subtract函数。因为-4是负四。
打印函数
函数通常不能打印,因为函数不是Show类型类的实例。除非这个函数被实现了。

ghci猜测是不是参数少了呢?但是实际上这个异常的内容是第一句话。
lambda
一次性匿名函数,这很常见。
有时候需要给高阶函数传递一个特定功能的函数,用lambda。写法是反斜杠\,后面跟参数列表,参数之间用空格分隔,->后面是函数体。通常也会把整个lambda用括号括起来。
举例如下:
numLongChains :: Int
numLongChains = length (filter (\xs -> length xs > 15) (map chain [1..100]) )
-- chain函数用于求克拉兹序列
实际上lambda函数和柯里函数+部分应用效果几乎相同,还是选更易读的。
lambda也能使用模式匹配,但只能使用一种模式。确保输入一定正确。
折叠函数
折叠允许将一个数据结构(如列表)规约为单个值。所有遍历列表中元素并据此返回一个值的操作都可以基于折叠实现。折叠取一个二元函数,一个初值(累加值)和一个待折叠的列表。
foldl左折叠
每次取列表的左端值不断累加处理。如这个sum函数的实现:
sum' :: (Num a) => [a] -> a
sum' xs = foldl (\acc x -> acc + x) 0 xs
--sum' foldl (+) 0 这是柯里函数的写法,更简单
foldr右折叠
累加从列表右端开始,二元函数的参数顺序也是反的(第一个为列表值,第二个为累加值)。
由于使用++往列表后追加元素的效率比使用:低,所以生成新列表时候通常使用右折叠。
foldl1和foldr1
行为差不多,只是不用提供初值,默认为第一个(或者最后一个)为初始值。
$ 函数应用符
先看定义:
($) :: (a -> b) -> a -> b
f $ x = f x
用空格隔开的函数应用有最高的优先级,是左结合的;用$的优先级最低,是右结合的。
直白的说就是分隔参数,减少括号的数量。这个在之前好像写过。
函数组合
$$
(f ·g)(x)=f(g(x))
$$
这是数学里的函数组合。也就是先拿参数调用一个函数,然后取结果作为参数调用下一个函数。
进行函数组合的函数为 .,定义如下:
(.) :: (b -> c) -> (a -> b) -> a -> c
f . g = \x -> f (g x)
注意要求f的参数类型和g的返回值类型相同。即组合函数的参数与g相同,返回值与f的相同。
组合函数用于生成新函数并且传递给其他函数。当然lambda也可。
对于有多个参数的函数,使用部分应用使每个函数都只用一个参数即可。
其实不是很理解。用括号的方式不必这个易懂吗?何必从括号方式缩减为.呢
pointless风格
等号两端都有的参数,由于柯里化可以同时省掉。但是函数声明还是要写清楚的:
sum' :: (Num a) => [a] -> a
sum' = foldl (+) 0
fn x = ceiling (negate (tan (cos (max 50 x))))
fn = ceiling . negate . tan . cos . max 50
模块
import Name 必须放在任何函数定义前。
可以用括号包围,选择性的导入;用hiding可以忽略某些函数的导入。
import qualified Name as N,避免导入Name中已经存在于当前空间下的函数。N是简写名字
编写可导出的模块
有区分自用函数和导出函数。
模块开头先定义模块名称(注意格式,用括号包围导出函数名,最后要加where),应该与文件名保持一致。接下来列出导出的函数,最后编写函数的实现。
module Geometry
( sphereVolume,
sphereArea,
cubeVolume,
cubeArea,
cuboidArea,
cuboidVolume
) where
sphereVolume :: Floating a => a -> a
sphereVolume radius = (4.0/3.0) * pi * (radius^3)
sphereArea :: Floating a => a -> a
sphereArea radius = 4 * pi * (radius ^2)
cubeVolume :: Num a => a -> a
cubeVolume side = cuboidVolume side side side
cubeArea :: Num a => a -> a
cubeArea side = cuboidArea side side side
cuboidArea :: Num a => a -> a -> a -> a
cuboidArea a b c = rectArea a b * 2 + rectArea b c * 2 + rectArea a c * 2
cuboidVolume :: Num a => a -> a -> a -> a
cuboidVolume a b c = rectArea a b * c
rectArea :: Num a => a -> a -> a
rectArea a b = a * b
导入只需要一行import即可。该文件必须与导入他的文件位于同一目录中。
当然也可以分层组织:先建立一个Geometry的文件夹,首字母大写;文件夹下新建三个文件,module名字写为 Geometry.Sphere这样的。接下来的调用就可以使用import Geometry.Sphere 了。
类型与类型类
使用data 关键字来定义一个新的数据类型。标准库中的Bool是这样定义的:
data Bool = True | False
等号左端是类型名称;右端是值构造器,指明改类型可能的值。类型名与值构造器首字母必须大写。
值构造器
值构造器本质上是一个返回某数据类型值的函数。数据类型中的字段其实对应着值构造器的参数。
data Shape = Circle Float Float Float | Rectangle Float Float Float Float

写个函数
area :: Shape -> Float
area (Circle _ _ r) = pi * r ^ 2
area (Rectangle x1 y1 x2 y2) = (abs $ x2 - x1) * (abs $ y2 - y1)
该函数的类型声明表示参数类型是Shape而不是Circle或者Rectangle,因为这两个是指构造器而不是类型。
data Shape = Circle Float Float Float | Rectangle Float Float Float Float
deriving (Show)
先这么写,该类型会被置于Show类型类中。
借助其他数据类型优化
data Point = Point Float Float deriving (Show)
data Shape = Circle Float Float Float | Rectangle Point Point deriving (Show)
Point 类的类型与构造器是同名的,这种情况在类型只有一种值构造器时很常见。
area函数修改如下
area :: Shape -> Float
area (Circle _ _ r) = pi * r ^ 2
area (Rectangle Point (x1 y1) Point (x2 y2)) = (abs $ x2 - x1) * (abs $ y2 - y1)
修改值
例如表示移动图形的函数?实现上是返回一个新位置的新图形。
nudge (Circle (Point x y) r) a b = Circle (Point (x+a) (y+b)) r
导出
把类型名当函数一样加到module的括号里面就好。用括号标识要导出的值构造器,也可以用..表示全导出。
module Shapes
( Point(..)
, Shape(..)
, area
.....
)
如果不带括号的话,就不导出任何值构造器,只能通过导出的构造辅助函数来的到Shape。比如Data.Map就不能用值构造器,只能用Map.fromList来构造新的映射。
记录语法
花括号登场了。先看例子
data Person = Person { firstname :: String
, lastname :: String
, age :: Int
, height :: Float
, phone :: String
, flavor :: String
} deriving (Show)
这样写可以自动创建函数,允许按字段取值。比如:
age :: Person -> Int
age (Person _ _ age _ _ _) = age
该函数可以被自动实现。
此外,使用记录语法实现的类型,在Show里面会被更清楚的输出。
类型构造器
类型构造器是取类型为参数,产生新的类型。C++的模板跟这个就很像。
data Maybe a = Nothing | Just a
Maybe 本身不是类型,要想成为类型,需要把类型参数填满。
在不关心数据类型中存储内容的类型时,用类型参数。比如说一个类型的行为与容器相似。
Haskell要求不能再data声明中添加类约束。
派生
在Haskell中的派生,含义大有不同。类型类像是一个接口,通过思考我们自定义数据类型是否能符合这个类型类的行为,从而决定是否让它派生为类型类的实例。这个过程与OOC中的interface还是很像的。
实现上,在构造数据类型后加上deriving关键字,Haskell会帮助这个类型派生出响应的行为。
data Person = Person {
firstname :: String,
lastname :: String,
age :: Int,
} deriving (Eq)
一个类派生为Eq的实例后,就可以使用==盒/=来判断相等性了。这里面会先现检查两个值的值构造器是否一致,在检查每一对字段数据是否相等(当然也得属于Eq类型类)。
- Show类型类要求参数必须都属于Read和Show;Read是指可以从字符串转为类型值
- Ord的比较大小除了已知的,还包括值构造器中的前后顺序。
- Enum类型类表示值可以拥有前驱和后继,Bounded表示值存在最大和最小值
类型别名
使用type关键字来创建一个类型别名:
type String = [Char]
说白了就是#define
这玩意甚至还能有参数!
type AssocList k v = [(k,v)]
AssocList作为一个类型构造器,取两个类型做参数,生成一个具体类型。
这有点麻烦,先跳过。
运算符重载
固定性声明被写在类型声明上面一行。运算符重载实际上是将一个函数定义为运算符,此时要加一个固定性规则。固定性规则包括优先级和结合性。
infixr 5 :-:
data List a = Empty | a :-: (List a) deriving (Show, Read, Eq, Ord)
等级这个事不太好说,不过有括号我也懒得管了。注意左右结合性。
继续深入类型类
Eq类型类的定义如下:
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
x == y = not (x/=y)
x /= y = not (x == y)
class关键字用于定义新的类型类,a为类型变量。类型类中给出的函数类型也不是实际的类型,函数体实现可选。就是这种交叉递归的形式非常费解。
如果要将类型类实现为实例,如下:
instance Eq TrafficLight where
Red == Red = True
Green == Green = True
Yellow == Yellow = True
_ == _ = False
实现的时候,将a替换成了具体的类型。
继续解释交叉递归定义的==和/= .这两种定义相互依赖,因此只需要在实例声明中覆盖其中的一个函数即可。这种风格称为类型类的最小完备定义。如果没有这个交叉递归,那就需要把两个都实现。
因此在实现中,只列出相等为true的组合,最后留一个万能的模式匹配。
再写一个实现Show的例子。
instance Show TrafficLight where
show Red = "red light"
....
当然直接派生Eq也是相同的。直接派生Show,会把值构造器的名字转成字符串。想写的其他还是要手动生成。
子类化
一个类型类实现为另一个类型类的子类。只需要在类型类的生命中添加一条类约束。
class (Eq a) => Num a where
....
意思就是:在将一个类型实现为Num的实例前,必须将其实现为Eq的实例。
组合IO操作
<-语法使得从IO操作中取得内容。用于执行IO操作并为结果绑定名字。
如果为纯函数式代码的返回值绑定名字则使用let。示例如下
main = do
putStrLn "hello"
name <- getLine
putStrLn ("hey, "++ name ++ "you rock!")
let bigName = map toUpper name
smallName = map toDown name
putStrLn ("hey,"++ bigName ++ smallName)
do和<- 是monad的语法糖,这个马上就来。
函子
完全看不懂,跳过
Monoid 幺半群、单位半群
对于一个二元函数,单位元+结合律
其类型类定义如下:
class Monoid m where
mempty :: m --单位元
mappend :: m -> m -> m --不是追加,而是取两个值返回第三个值
mconcat :: [m] -> m --
mconcat = foldr mappend mempty
monoid定律
需要满足以下三条:
mempty `mappend` x = x
x `mappend` mempty = x
(x `mappend` y) `mappend` z = x `mappend` (y `mappend` z)
示例
列表是monoid,任何类型的都是。monoid要求实例是具体类型,所以写的是[a]
instance Monoid [a] where
mempty = []
mappend = (++)
对于乘法,单位元是1;对于加法,单位元是0。这是很自然的。当我们面对需要把“一个类型变成某个类型类的实例”时,可以使用newtype关键字,将原类型变成类型类的实例。
Data.Monoid对于数有两个导出类型:Product和Sum。对于任何Num的实例a,Product a都是Monoid的实例。Sum也是类似的。
对于Bool,可以有两种方式成为monoid:
- 逻辑或||为二元函数,False为单位元
- 这种方式得到了Any newtype
- 逻辑与&&为二元函数,True为单位元。
- 这种得到了All newtype
对于Ordering,不是很直观,看一下定义:
instance Monoid Ordering where
mempty = EQ
LT `mappend` _ = LT
EQ `mappend` y = y
GT `mappend` _ = GT
可以用单词字母比较来理解:首字母不同就可以决定;相同则要继续比较下面的。这个mappend函数不满足交换律。这背后其实是认为更重要的比较准则放在左边。



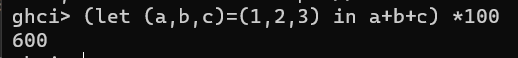

 浙公网安备 33010602011771号
浙公网安备 33010602011771号