抽样分布

统计量

统计学中最主要的提取信息的方式就是对原始信息进行一定的运算，得出某些代表性的数字，以反映数据某些方面的特征，这种数字被称为统计量。用统计学语言表述，统计量是样本的函数，它不依赖于任何未知函数。推断统计学的重要作用就是，通过从总体中抽取样本构造适当的统计量。

常用统计量

 

 

抽样分布

在总体X的分布类型已知时，若对任一自然数n都能导出统计量的分布的数学表达式，这种分布称为精确的抽样分布。它对样本量n较小的统计推断问题非常有用。精确的抽样分布大多是在正态总体情况下得到的。在正态总体条件下，主要有分布，t分布，F分布，称为统计三大分布。

卡方分布(Chi-square distribution)

定义： 

　　设随机变量相互独立，且服从标准正态分布N(0,1)，则它们的平方和服从自由度为n的分布，读作卡方分布。

 

自由度是统计学中常用的一个概念，它可以解释为独立变量的个数，还可解释为二次型的秩[2]。例如，是自由度为1的分布，；是自由度为n的分布，。

 

 

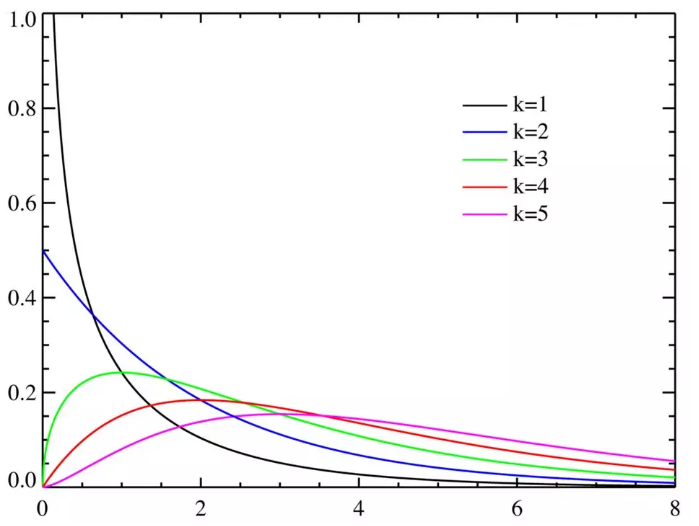
 分布的数学期望为：

分布的方差为：

分布具有可加性，即若，，且独立，则

当自由度足够大时，分布的概率密度曲线趋于对称。当时，分布的极限分布是正态分布。

t分布(t distribution)

定义： 

设随机变量，，且X与Y独立，则

该分布称为t分布，记为t(n)，其中，n为自由度。

 

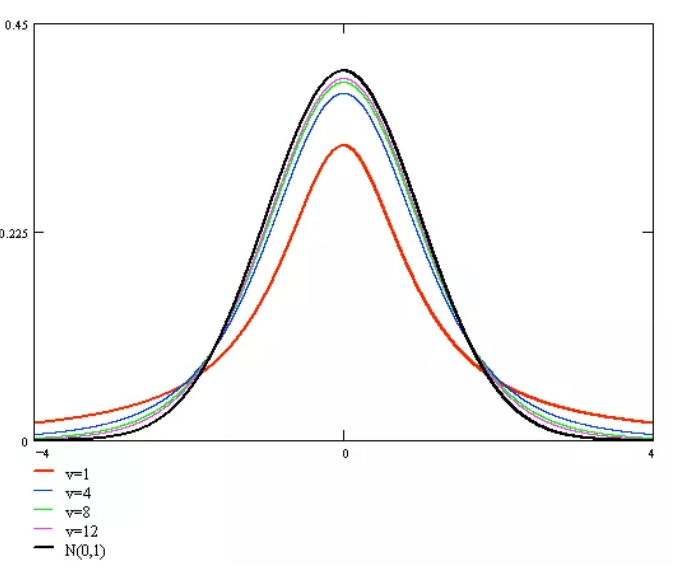
 当时，t分布的数学期望。当时，t分布的方差。

从上图可以看出，t分布的密度函数曲线与标准正态分布的密度函数曲线非常相似，都是单峰偶函数。只是，的密度函数的两侧尾部要比的两侧尾部粗一些。的方差比的方差大一些。

F分布(F distribution)

定义： 

设随机变量Y与Z相互独立，且Y和Z分别服从自由度为m和n的卡方分布，随机变量X有如下表达式：

则称X服从第一自由度为m，第二自由度为n的F分布，记为，简记为。F分布的密度函数的图形如下图。

 

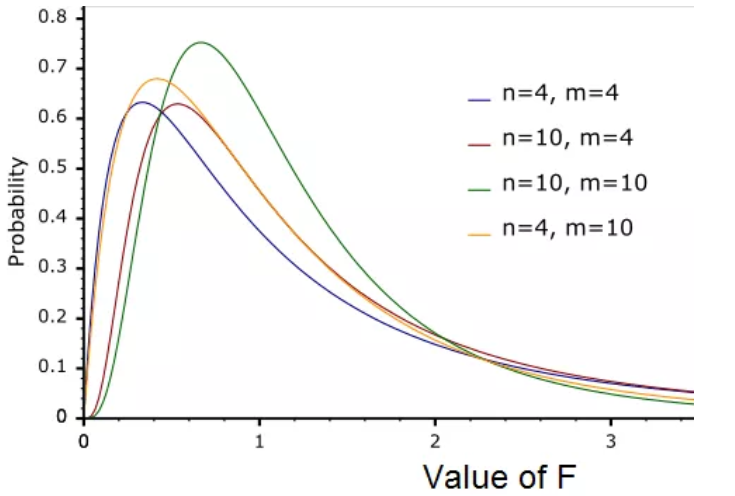
 设随机变量X服从分布，则数学期望和方差分别为：

样本均值的分布与中心极限定理

当总体分布为正态分布时，可以得到下面的结果： 的抽样分布(sampling distribution)仍为正态分布，的数学期望为，方差为，则

上面的结果表明，的期望值与总体均值相同，而方差则缩小为总体方差的。这说明当用样本均值去估计总体均值时，平均来说没有偏差（这一点称为无偏性）；当n越来越大时，的散布程度越来越小，即用估计越来越准确。实际问题中，总体的分布并不总是正态分布或近似正态分布，此时的分布将取决于总体分布的情况。不过当抽样个数n比较大时，人们证明了如下的中心极限定理。该定理告诉我们不管总体的分布是什么，样本均值的分布总是近似正态分布，只要总体的方差有限。因为无论是什么总体分布，设总体均值为，总体方差为，总有：

所以当n比较大时，近似服从，等价地有

中心极限定理(central limit theorem) 定义：设从均值为、方差为(有限)的任意一个总体中抽取样本量为n的样本，当n充分大时，样本均值的抽样分布近似服从均值为、方差为的正态分布。

总结

中心极限定理的作用在大样本情况下，可以认为样本均值的抽样分布服从正态分布，从而完成样本均值概率的计算。

正态总体下的几个常用统计量的抽样分布，因为获得了较为完整的分布数据，一旦确认统计量符合这几类抽样分布，可以通过查表的方式对概率值进行计算。

 

转自：https://mp.weixin.qq.com/s/vxBYqAFxt0MTBcux1SZlxg