第三周：简单数据分布

 正态分布

简介

正态分布又名高斯分布它以数学天才 Carl Friedrich Gauss 命名正态分布又名高斯分布，越简单的模型越是常用，因为它们能够被很好的解释和理解。

正态分布非常简单，这就是它是如此的常用的原因。因此，理解正态分布非常有必要。

什么是概率分布

首先介绍一下相关概念：

考虑一个预测模型，该模型可以是我们的数据科学研究中的一个组件。

如果我们想精确预测一个变量的值，那么我们首先要做的就是理解该变量的潜在特性。

首先我们要知道该变量的可能取值，还要知道这些值是连续的还是离散的。简单来讲，如果我们要预测一个骰子的取值，那么第一步就是明白它的取值是1 到 6（离散）。

第二步就是确定每个可能取值（事件）发生的概率。如果某个取值永远都不会出现，那么该值的概率就是 0 。事件的概率越大，该事件越容易出现。

在实际操作中，我们可以大量重复进行某个实验，并记录该实验对应的输出变量的结果。我们可以将这些取值分为不同的集合类，在每一类中，我们记录属于该类结果的次数。

 

例如：

我们可以投10000次骰子，每次都有6种可能的取值，我们可以将类别数设为6，然后我们就可以开始对每一类出现的次数进行计数了。

我们可以画出上述结果的曲线，该曲线就是概率分布曲线。目标变量每个取值的可能性就由其概率分布决定。

一旦我们知道了变量的概率分布，我们就可以开始估计事件出现的概率了，我们甚至可以使用一些概率公式。至此，我们就可更好的理解变量的特性了。

概率分布取决于样本的一些特征，例如平均值，标准偏差，偏度和峰度。如果将所有概率值求和，那么求和结果将会是100%；

世界上存在着很多不同的概率分布，而最广泛使用的就是正态分布了。

初遇正态分布

我们可以画出正态分布的概率分布曲线，可以看到该曲线是一个钟型的曲线。如果变量的均值，模和中值相等，那么该变量就呈现正态分布。

如下图所示，为正态分布的概率分布曲线：

理解和估计变量的概率分布非常重要，下面列出的变量的分布都比较接近正态分布：
人群的身高成年人的血压传，播中的粒子的位置测量误差，回归中的残差，人群的鞋码，一天中雇员回家的总耗时，教育指标，
此外，生活中有大量的变量都是具有 x % 置信度的正态变量，其中，x<100。

 什么是正态分布

正态分布只依赖于数据集的两个特征：样本的均值和方差。

均值：样本所有取值的平均
方差：该指标衡量了样本总体偏离均值的程度
正态分布的这种统计特性使得问题变得异常简单，任何具有正态分布的变量，都可以进行高精度分预测。
值得注意的是，大自然中发现的变量，大多近似服从正态分布。
 
正态分布很容易解释，这是因为：
正态分布的均值，模和中位数是相等的。我们只需要用均值和标准差就能解释整个分布。正态分布是我们熟悉的正常行为。

 为何如此多的变量都大致服从正态分布

这个现象可以由如下定理解释：

当在大量随机变量上重复很多次实验时，它们的分布总和将非常接近正态分布。

由于人的身高是一个随机变量，并且基于其他随机变量，例如一个人消耗的营养量，他们所处的环境，他们的遗传等等，这些变量的分布总和最终是非常接近正态的。
这就是中心极限定理。
 
本文的核心：
我们从上文的分析得出，正态分布是许多随机分布的总和。
如果我们绘制正态分布密度函数，那么它的曲线将具有以下特征：

如上图所示，该钟形曲线有均值为 100，标准差为1：

均值是曲线的中心。这是曲线的最高点，因为大多数点都是均值。曲线两侧的点数相等。

曲线的中心具有最多的点数。曲线下的总面积是变量所有取值的总概率。因此总曲线面积为 100％

 

更进一步，如下图所示：

约 68.2％ 的点在 -1 到 1 个标准偏差范围内。
约 95.5％ 的点在 -2 到 2 个标准偏差范围内。
约 99.7％ 的点在 -3 至 3 个标准偏差范围内。
这使我们可以轻松估计变量的变化性，并给出相应置信水平，它的可能取值是多少。
例如，在上面的灰色钟形曲线中，变量值在 99-101 之间的可能性为 68.2％。

正态分布函数

正态分布是钟形曲线，其中mean = mode = median。

如果使用概率密度函数绘制变量的概率分布曲线，则给定范围的曲线下的面积，表示目标变量在该范围内取值的概率。
概率分布曲线基于概率分布函数，而概率分布函数本身是根据诸如平均值或标准差等多个参数计算的。我们可以使用概率分布函数来查找随机变量取值范围内的值的相对概率。
例如，我们可以记录股票的每日收益，将它们分组到适当的集合类中，然后计算股票在未来获得20-40％收益的概率。
标准差越大，样品中的变化性越大。

使用 Python 探索变量的概率分布

最简单的方法是使用pandas中的df.hist(bins=10)：

import  pandas as pd
df = pd.read_csv('test.csv')
df.hist(bins=10)
#Make a histogram of the DataFrame.
该函数向我们展示了所有变量的概率分布。

变量服从正态分布意味着什么

如果我们将大量具有不同分布的随机变量加起来，所得到的新变量将最终具有正态分布。这就是前文所述的中心极限定理。
服从正态分布的变量总是服从正态分布。例如，假设 A 和 B 是两个具有正态分布的变量，那么：
A x B 是正态分布A + B 是正态分布
因此，使用正态分布，预测变量并在一定范围内找到它的概率会变得非常简单。

样本不服从正态分布怎么办

我们可以将变量的分布转换为正态分布,我们有多种方法将非正态分布转化为正态分布：
1. 线性变换
一旦我们收集到变量的样本数据，我们就可以对样本进行线性变化，并计算Z得分：
计算平均值计算标准偏差对于每个 x，使用以下方法计算 Z：

2. 使用 Boxcox 变换

我们可以使用 SciPy 包将数据转换为正态分布：
scipy.stats.boxcox(x, lmbda=None, alpha=None)

3. 使用 Yeo-Johnson 变换
另外，我们可以使用 yeo-johnson 变换。

Python 的 sci-kit learn 库提供了相应的功能：

sklearn.preprocessing.PowerTransformer(method=’yeojohnson’,standardize=True, copy=True)

正态分布的问题

由于正态分布简单且易于理解，因此它也在预测研究中被过度使用。假设变量服从正态分布会有一些显而易见的缺陷。
例如，我们不能假设股票价格服从正态分布，因为价格不能为负。因此，我们可以假设股票价格服从对数正态分布，以确保它永远不会低于零。
 
我们知道股票收益可能是负数，因此收益可以假设服从正态分布。
假设变量服从正态分布而不进行任何分析是愚蠢的。
变量可以服从Poisson，Student-t 或 Binomial 分布，盲目地假设变量服从正态分布可能导致不准确的结果。

二项分布式

概念

二项分布是一种具有广泛用途的离散型随机变量的概率分布，它是由贝努里始创的，所以又叫贝努里分布。

二项分布是指统计变量中只有性质不同的两项群体的概率分布。所谓两项群体是按两种不同性质划分的统计变量，是二项试验的结果。

即各个变量都可归为两个不同性质中的一个，两个观测值是对立的。因而两项分布又可说是两个对立事件的概率分布。

二项分布的解析

二项分布用符号b(x．n．p)，表示在n次试验中有x次成功，成功的概率为p。

　　二项分布的概率函数可写作：

　　b(x．n．p)=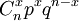C_n^xp^xq^{n-x}

　　式中x＝0、1、2、3．．．．．n为正整数

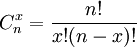
　　C_n^x=\frac{n!}{x!(n-x)!}

　　两项分布中含有两个参数n与p，当它们的值已知时，便可计算出分布列中各概率的值。

例1 掷硬币试验。有10个硬币掷一次，或1个硬币掷十次。问五次正面向上的概率是多少?

　　解：根据题意n＝10，p＝q＝1/2，x＝5

　　b(5、l0、1/2) = 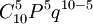C_{10}^5 P^5 q^{10-5}

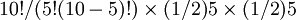
　　= 10! / (5!(10-5)!) \times (1/2)5 \times (1/2)5

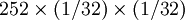
　　= 252 \times (1/32) \times (1/32)

　　= 0．24609

　　所以五次正面向上的概率为0．24609

例2  此题若问五次及五次以上正面向上的概率是多少?

　　解：此题要求出五次及五次以上正面向上的概率之和。正面有五次、六次、七次、八次、九次、十次。依公式5—10应为：

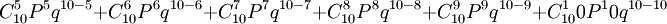
　　C_{10}^5 P^5 q^{10-5}+ C_{10}^6 P^6 q^{10-6} + C_{10}^7 P^7 q^{10-7} + C_{10}^8 P^8 q^{10-8}+C_{10}^9 P^9 q^{10-9}+ C_{10}^10 P^10 q^{10-10}

　　= 252/1024+210/1024+120/1024+45/1024+10/1024+1/1024

　　= 638/1024

　　= 0．623

　　五次及五次以上正面向上的概率为0．623

参考：https://wiki.mbalib.com/wiki/%E4%BA%8C%E9%A1%B9%E5%88%86%E5%B8%83

泊松分布

什么是泊松分布

Poisson分布(法语：loi de Poisson，英语：Poisson distribution，译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等)，

是一种统计与概率学里常见到的离散机率分布(discrete probability distribution)，由法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年时发表。

泊松分布函数

泊松分布的概率质量函数为：

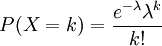
　　P(X=k)=\frac{e^{-\lambda} \lambda^k}{k!}

　　泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。

 

泊松分布适合于描述单位时间内随机事件发生的次数。

如某一服务设施在一定时间内到达的人数，电话交换机接到呼叫的次数，汽车站台的候客人数，机器出现的故障数，自然灾害发生的次数等等。

 

若随机变量X取0和一切正整数值，在n次独立试验中出现的次数x恰为k次的概率P（X=k）=（k=0,1,...,n），式中λ是一个大于0的参数，此概率分布称为泊松分布。

它的期望值为E(x)=λ，方差为D(x) = λ。当n很大，且在一次试验中出现的概率P很小时，泊松分布近似二项分布。

参考：https://wiki.mbalib.com/wiki/%E6%B3%8A%E6%9D%BE%E5%88%86%E5%B8%83

均匀分布

在概率论和统计学中，均匀分布也叫矩形分布，它是对称概率分布，在相同长度间隔的分布概率是等可能的。

均匀分布由两个参数a和b定义，它们是数轴上的最小值和最大值，通常缩写为U（a，b）。

概率密度函数

均匀分布的概率密度函数为：
在两个边界a和b处的f（x）的值通常是不重要的，因为它们不改变任何
  
的积分值。 概率密度函数有时为0，有时为
  
。 在傅里叶分析的概念中，可以将f（a）或f（b）的值取为
  
，因为这种均匀函数的许多积分变换的逆变换都是函数本身。 [1] 
对于平均值μ和方差
  
，概率密度可以写为：

分布函数

累积分布函数为：
它的逆是：
 
参考：https://baike.baidu.com/item/%E5%9D%87%E5%8C%80%E5%88%86%E5%B8%83/954451

卡方分布

卡方分布 (χ2分布)是概率论与统计学中常用的一种概率分布。

k 个独立的标准正态分布变量的平方和服从自由度为k 的卡方分布。卡方分布常用于假设检验和置信区间的计算。

数学定义

若k 个随机变量Z1、……、Zk 相互独立，且数学期望为0、方差为 1(即服从标准正态分布)，则随机变量X

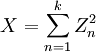
X=\sum_{n=1}^k Z_n^2

被称为服从自由度为 k 的卡方分布，记作

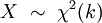
X\ \sim\ \chi^2(k)

卡方分布特征

卡方分布的概率密度函数为：

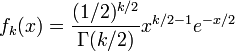
f_k(x)= \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}

其中x≥0, 当x≤0时fk(x) = 0。这里Γ代表Gamma 函数。

参考：https://wiki.mbalib.com/wiki/%E5%8D%A1%E6%96%B9%E5%88%86%E5%B8%83

beta（贝塔）分布

用一句话来说，beta分布可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小。

举一个简单的例子：

熟悉棒球运动的都知道有一个指标就是棒球击球率(batting average)，就是用一个运动员击中的球数除以击球的总数，

我们一般认为0.266是正常水平的击球率，而如果击球率高达0.3就被认为是非常优秀的。

现在有一个棒球运动员，我们希望能够预测他在这一赛季中的棒球击球率是多少。

你可能就会直接计算棒球击球率，用击中的数除以击球数，但是如果这个棒球运动员只打了一次，而且还命中了，那么他就击球率就是100%了，
这显然是不合理的，因为根据棒球的历史信息，我们知道这个击球率应该是0.215到0.36之间才对啊。

对于这个问题，我们可以用一个二项分布表示（一系列成功或失败），一个最好的方法来表示这些经验（在统计中称为先验信息）就是用beta分布，
这表示在我们没有看到这个运动员打球之前，我们就有了一个大概的范围。beta分布的定义域是(0,1)这就跟概率的范围是一样的。

接下来我们将这些先验信息转换为beta分布的参数，我们知道一个击球率应该是平均0.27左右，

而他的范围是0.21到0.35，那么根据这个信息，我们可以取α=81,β=219

之所以取这两个参数是因为：

  • beta分布的均值是\frac{\alpha}{\alpha+\beta}=\frac{81}{81+219}=0.27
  • 从图中可以看到这个分布主要落在了(0.2,0.35)间，这是从经验中得出的合理的范围。

在这个例子里，我们的x轴就表示各个击球率的取值，x对应的y值就是这个击球率所对应的概率。也就是说beta分布可以看作一个概率的概率分布。

参考：http://www.360doc.com/content/16/1228/10/38911980_618347839.shtml

 

posted @ 2019-08-04 23:22  ZhuGaochao  阅读(1138)  评论(0)  编辑  收藏  举报