XGBoost 入门系列第一讲

*本文旨在普及机器学习的使用，对于文章涉及到的模型策略不具有实盘参考意义，感兴趣朋友可以前往BigQuant人工智能量化投资平台进一步学习。

Boosted Trees 介绍

XGBoost 是 “Extreme Gradient Boosting”的简称，其中“Gradient Boosting”来源于附录1.Friedman的这篇论文。本文基于 gradient boosted tree ，中文可以叫梯度提升决策树，下面简称GBDT，同时也有简称GBRT，GBM。针对gradient boosted tree的细节也可以参考附录2.这篇网页。

监督学习

XGBoost 主要是用来解决有监督学习问题，此类问题利用包含多个特征的训练数据 $x_i$，来预测目标变量 $y_i$。在我们深入探讨GBDT前，我们先来简单回顾一下监督学习的一些基本概念。

模型与参数

在监督学习中模型（model）表示一种数学函数，通过给定 $x_i$ 来对 $y_i$ 进行预测。以最常见的线性模型（linear model）举例来说，模型可以表述为 $\widehat{y_i}={\sum }_j{\theta }_j{x}_{ij}$，这是一个输入特性进行线性加权的函数。那么针对预测值的不同，可以分为回归或者分类两种。
在监督学习中参数（parameters）是待定的部分，我们需要从数据中进行学习得到。在线性回归问题中，参数用$\theta$来表示。

目标函数：训练误差 + 正则化

根据对 $y_i$的不同理解，我们可以把问题分为，回归、分类、排序等。我们需要针对训练数据，尝试找到最好的参数。为此，我们需要定义所谓的目标函数，此函数用来度量参数的效果。
这里需要强调的是，目标函数必须包含两个部分：训练误差和正则化。
$$Obj(\Theta )=L(\theta )+\Omega (\Theta )$$
其中，$L$表示训练误差函数，$\Omega$表示正则项。训练误差用来衡量模型在训练数据上的预测能力。比较典型的有用均方差来衡量。
$$L(\theta )=\sum _i(y_i-\widehat{y_i}{)}^2$$
另外针对逻辑回归，比较常见的损失函数为Logistic函数：
$$L(\theta )=\sum _i[y_i\ln (1+e^{-\widehat{y_i}})+(1-y_i)\ln (1+e^{\widehat{y_i}})]$$
另外一个比较重要的部分就是正则项，这也是很多人容易忘记的部分。正则项是用来控制模型的复杂度，以防止过拟合（overfitting）。这听起来有点抽象，那么我们用下面的例子来说明。针对下面左上角的这幅图，我们需要找到一个阶梯函数来拟合图中的数据点集合。那么问题来了，下面剩下的三幅图中，哪一个你认为是最好的呢？

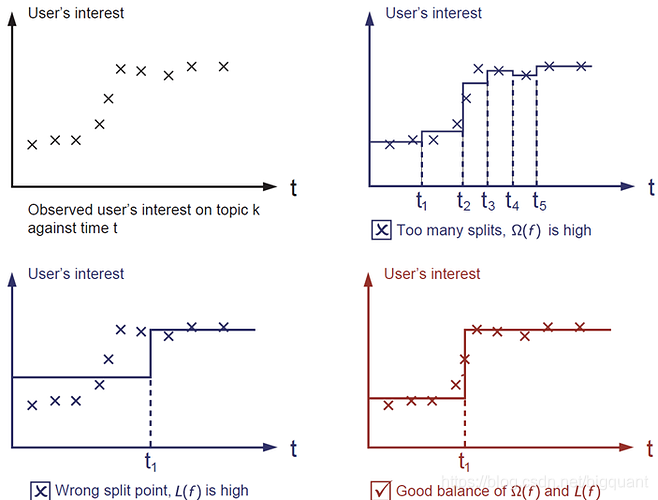
答案是用红色标注出来的这幅图。为什么呢？因为我们对于好的模型的判断依据是 简单（simple）并且 准确（predictive）。但这两者又是相互矛盾的，在机器学习中我们也把这两者也用 bias-variance 来表述。

复合树模型（Tree Ensemble）

在前面我们已经介绍了监督学习，现在让我们开始了解树模型。首先先来了解一下xgboost所对应的模型：复合树模型。复合树模型是一组分类和回归树（classification and regression trees - CART）。这里我们举CART中的一个例子，一类分类器用来辨别某人是否喜欢计算机游戏。

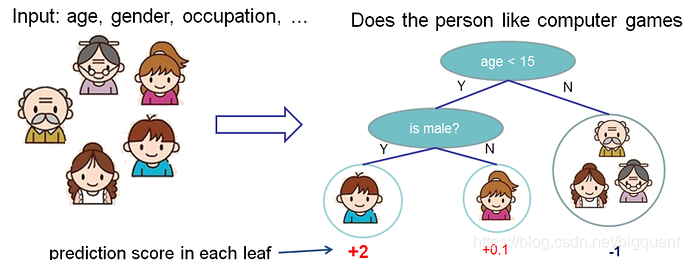
我们把家庭中的成员分到了不同的叶子节点，同时每个叶子节点上都有一个分数。CART与决策树相比，细微差别在于CART的叶子节点仅包含判断分数。在CART中，相比较于分类结果，每个叶子节点的分数给我们以更多的解释。这让CART统一优化节点更为容易，这在后面会有具体介绍。
通常情况下，在实践中往往一棵树是不够用的。这个时候往往需要把多棵树的预测结果综合起来，这就是所谓的复合树模型。

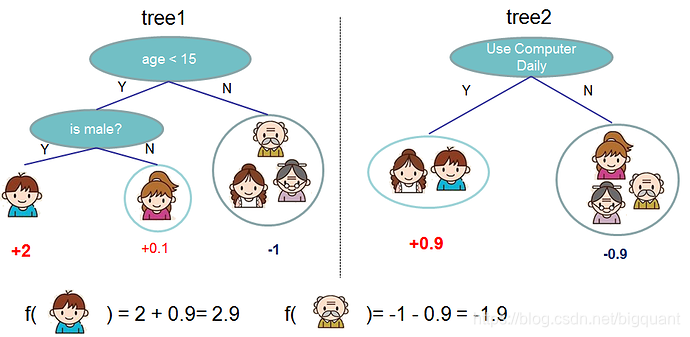
上面就是由两棵树组成的复合树的例子。每棵树上的分数简单相加就得到了最终的分数。用数学式子可以表达如下：
$$\widehat{y_i}=\sum _{k=1}^K{f}_k(x_i),f_k\in \mathcal{F}$$
$K$表示树的数目，$f$是函数空间$F$中的一个函数，$F$表示CART的所有可能集合。所以我们的优化目标可以写作：
$$\text{obj}(\theta )=\sum _i^{n}l(y_i,\widehat{y_i})+\sum _{k=1}^K\Omega (f_k)$$
现在问题来了，随机森林对应的模型是什么呢？对了，也是复合树模型。所以在模型的表述上，随机森林和提升树是一样的，他们俩的区别只是在于如何训练。这也就意味着，如果要写一个关于复合树模型的预测服务，我们只需要写一个就可以同时支持随机森林和提升树。

提升树 （Tree Boosting）

介绍了模型之后，让我们看看训练部分。那么我们是怎么训练这些树的呢？对于所有的监督学习模型，答案也都是同样，只需要做两件事，定义目标函数，然后优化它。
假设我们有如下的目标函数（需要切记目标函数必须包含损失函数及正则项）
$$\text{obj}=\sum _{i＝1}^{n}l(y_i,{\widehat{y_i}}^{(t)})+\sum _{k=1}^t\Omega (f_i)$$

增量训练 （Additive Training）

首先我们需要问的是，这些树的参数是什么？我们会发现，我们所要学习的就是这些 $f_i$方法，每个方法中定义树的结构以及叶子节点的分数。这比传统最优化问题要更难，传统最优化问题我们可以通过梯度来解决。而且我们无法在一次训练所有的树。相反，我们用增量（additive）的方式：每一步我们都是在前一步的基础上增加一棵树，而新增的这棵树是为修复上一颗树的不足。，我们把每$t$步的预测用${\widehat{y_i}}^{(t)}$表示，这样我们就有了：

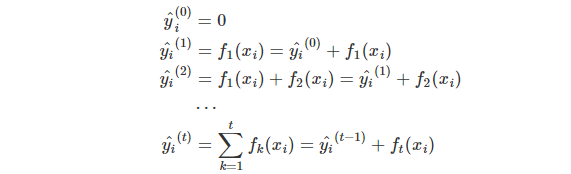
这里还有疑问的是，在每一步中如何确定哪棵树是我们需要的呢？一个很自然的想法就是，增加这棵树有助于我们的目标函数。

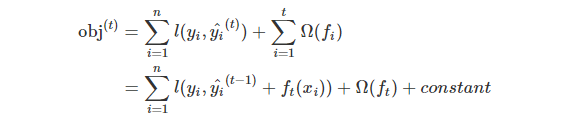
我们用MSE（均方差）作为损失函数，这样式子就变成了：

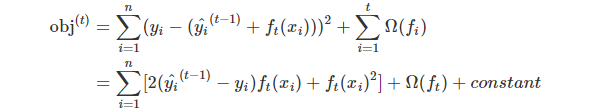
对于用MSE求出来的损失函数式子比较友好，包含一个一阶项和一个二次项。但是对于其他形式，就很难推导出这么友好的损失函数式子了。那么针对这种情形，我们就用泰勒展开公式（参考附录4，$x$取值${\widehat{y_i}}^{(t-1)}+f_t(x_i)$，$a$取值${\widehat{y_i}}^{(t-1)}$）来逼近：
$${\text{obj}}^{(t)}=\sum _{i=1}^n[l(y_i,{\widehat{y_i}}^{(t-1)})+g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\Omega (f_t)+constant$$
其中 $g_i$ 和 $h_i$ 定义如下：

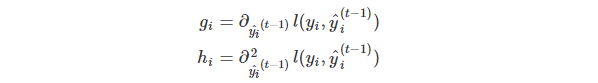
然后针对上述式子，我们删除常数项，那么在 $t$ 目标函数就变成：
$$\sum _{i=1}^n[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\Omega (f_t)$$
选择新的一棵树，上述式子就是优化目标。这样的优化目标有一个优点，式子只需要考虑$g_i$和$h_i$。这就是xgboost为什么能支持自定义损失函数的原因。我们能够优化每一个损失函数，包括逻辑回归和加权逻辑回归，只需要把对应的$g_i$和$h_i$作为输入传入即可。

模型复杂度

现在讲讲正则化。那么如何定义 $\Omega (f)$呢，在此之前，我们需要定义 $f(x)$：
$$f_t(x)=w_{q(x)},w\in R^T,q:R^d\to \{1,2,\cdots ,T\}.$$
这里$w$表示叶子节点上的分数所组成的向量，$q$表示每个数据映射到相应叶子节点的对应关系函数，$T$表示叶子节点的数量。在XGBoost中，我们用如下公式定义复杂度：
$$\Omega (f)=\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$
当然还有其他公式来定义复杂度，但是我们发现上述式子在实践过程中表现很好。其他树相关的算法包不怎么认真对待正则化，甚至直接忽视掉。

如何计算树叶子节点上的分数

那么在增量学习过程中，如何选择这棵新增的树呢？要解决这个问题，我们先解决一下其中这个子问题：假设这棵树的结构已经确定了，如何来计算叶子节点上的分数？
这一部分是推广过程中比较神奇的一个步骤。根据上述过程，我们写出第$t$步树的目标值：

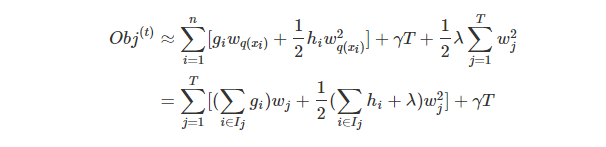
这里 $I_j=\{i|q(x_i)=j\}$表示每个映射到第$j$个叶子节点对应的数据样本。需要注意的是，因为映射到相同叶子节点上的数据样本他们的分数是相同的，所以在第二行我们改变了一下求和$\sum$顺序。同时我们令 $G_j={\sum }_{i\in I_j}{g}_i$ 以及 $H_j={\sum }_{i\in I_j}{h}_i$，那么上述公式简化为：
$${\text{obj}}^{(t)}=\sum _{j=1}^T[G_j{w}_j+\frac{1}{2}(H_j+\lambda )w_j^2]+\gamma T$$
在上述式子中，每一个$w_j$是相互独立的，那么针对一元二次方程 $G_j{w}_j+\frac{1}{2}(H_j+\lambda )w_j^2$ 而言，可以比较容易求出当新增的这棵树的结构 $q(x)$ 已知的情况下，目标函数最小值下的 $w_j$：

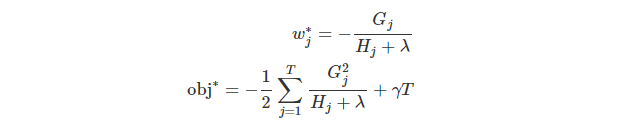
最后的式子计算的是树 $q(x)$ 的优劣：

如果上面的式子看着比较复杂的话，那么根据上面的这幅图来看如何计算这些分数，就会显得更直观些。一旦树的结构已知的话，我们只需要通过计算每个节点上的 $g_i$ 和 $h_i$ ，然后把各个叶子节点上的这些数值加起来，用上述方程式就可以计算这棵树的优劣了。

如何学习树的结构

现在我们已经知道一旦树的结构固定下来以后，如何来计算叶子节点上的分数，以及计算这棵树的优劣。那么关于现在我们要来解决如何来学习这棵树的结构。比较简单粗暴的方法就是遍历所有可能的树结构，然后从中找到最好的那棵树。但是这也是不切实际的，因为需要遍历的情况实在是太多了。所以我们来寻求一种贪婪的解法，就是在树的每个层构建的过程中，来优化目标。那么这里假设在某一层的构建过程中，假设特征已经选定，我们先如何进行二叉划分呢，以及是不是需要进行划分？我们可以通过下面的式子来计算划分之后，在目标上所获得的收益（这个收益越越好，负数表示收益为负）：
$$Gain=\frac{1}{2}\left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }\right]-\gamma$$
上面的这个式子可以分解为 1) 若是划分，划分后左边节点的收益 2) 或是划分，划分后右边节点的收益 3) 如不划分，原先节点的收益 4) 划分后正则项的收益。通过上述式子比较容易看到，当划分后叶子节点所带来的新增收益小于 $\gamma$ ，我们最好还是不要进行二叉划分，保留原样是最好的。这也是日后做剪枝的依据。
那么针对排序后的特征，我们所要做的就是遍历各种划分，找到一个最好的划分点，如下图表示。

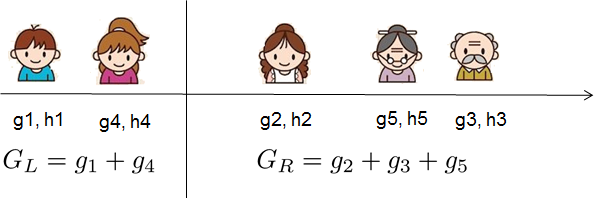
那么这里还有一个问题就是在构建树的结构过程中，在某一层如何进行特征选择呢？这里提供了一种比较简单的方式就是遍历每一种特征，然后根据上述式子的Gain，找到最大的Gain值对应的特征。

关于XGBoost的最后几句话

我们花了很长时间来讲解 Boosted Tree，那么XGBoost相较于Boosted Tree，又做了哪些额外的事情呢？XGBoost是遵循上述Boosted Tree思想的工程实现，但同时又考虑兼顾系统优化和机器学习原理，最大化的保证可扩展性、便捷性以及准确性。

---

原文链接：《XGBoost 入门系列第一讲》

BigQuant—人工智能量化投资平台