Alpha系列——从MPT到APT

实现平台：BigQuant—人工智能量化投资平台
可在文末前往原文一键克隆代码进行进一步研究

从MPT到APT

前面文章为大家介绍了许多AI量化投资理念，CAPM和APT是现代投资组合理论的基石，在这篇教程中，我们阐述了CML和CAPM的关系，以及APT和CAPM的差异和不同，从而帮助读者在正式理解主动投资管理框架之前，打好理论基础和知识。

夏普组合与CML

我们在上期的教程中，已经证明了最优夏普组合就是在有效前沿上夏普比最大的风险资产组合。然而可以证明，在EMH的假设条件下，且在均衡状态下，最优夏普组合就是市场组合（市值加权组合）。

不过关于这个论点，有几个大家需要注意的地方：

这个是有效市场假说下的推论，读者可以选择不相信这个假说
这里的市场组合包含了全市场所有的风险资产，如股票、期货、金属、外汇、房地产、古玩等等
有效前沿是一个凸函数，在投资者均方投资决策的条件下，任何偏离最优夏普组合的行为都会得到纠正

有了上述总结，相信大家对这个结论也会有自己的判断。为了阐述后面的内容，教程后面将视最优夏普组合与市场组合为同一个概念，但是大家心里要清楚这里的前提假设和背景。

现在，为了引出CML资本市场线的概念，我们在风险资产外，加入了无风险资产的概念。

然后我们要介绍一个非常重要的定律，即分离定理：
指在投资组合中可以以无风险利率自由借贷的情况下投资人选择投资组合时都会选择无风险资产和风险投资组合的得最优组合点，因为这一点相对于其他的投资组合在风险上或是报酬上都具有优势。
所以谁投资都会都会选择这一点。投资人对风险的态度，只会影响投入的资金数量，而不会影响最优组合点。

\begin{align*}
E[r_{p}] = w_{f} r_{f} + w_{m} E[r_{m}]
\end{align*}

\begin{align*}
其中，w_{f} + w_{m} = 1
\end{align*}

我们的组合方差为：

\begin{align*}
\sigma_{p}^2 &= w_{f}^2 \sigma_{f}^2 + w_{m}^2 \sigma_{m}^2 + 2 w_f w_m cov(r_f,r_m)\
&= w_{m}^2 \sigma_{m}^2\
\Rightarrow \quad w_m &= \frac{\sigma_{p}}{\sigma_{m}}
\end{align*}

于是，我们得到CML的显示表达式：

\begin{align*}
E[r_{p}] = r_{f} + \left[ \frac{E[r_{m}]-r_{f}}{\sigma_{m}} \right] \sigma_{p}
\end{align*}

风险溢价

上式中的 $\frac{E[r_{m}]-r_{f}}{\sigma_{m}}$ ，我们通常称之为风险溢价。分子表示超额收益，即超出无风险资产收益率的报酬，分母表示组合风险（标准差），
这个指标在经济意义上就是表示单位市场风险下的报酬，其实也是市场组合的夏普比率。CML的斜率预示了为了承担额外单位风险所需要支付的报酬，因此也被称为市场均衡价格下的风险。

换句话说，我可以可以这么理解和表示：

\begin{align*}
E[r_{p}] = r_{f} + 市场价格风险 \times 风险量
\end{align*}

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl

rf = 0.05                 # 无风险利率
mu = np.array([0.1,0.15,0.18]) # 预期收益率向量
sigma = np.array([0.1,0.12,0.15])
rou_ab, rou_ac, rou_bc = 0.2, 0.5, -0.2
# 协方差矩阵
C = np.array([[1,      rou_ab,  rou_ac],
              [rou_ab, 1,       rou_bc],
              [rou_ac, rou_bc,  1     ]])
V = np.outer(sigma,sigma)*C

# 前沿曲线绘图函数
def plot_efficient_frontier(rf=rf,mu=mu,V=V,is_subplot=False,show_E=False,strategy=None):
    f = mu-rf                 # 超额收益
    N = len(mu)
    e = np.ones(N)
    sigma = np.sqrt(np.diag(V))
    V_inverse = np.linalg.inv(V)
    # 等权投资组合
    w_E = e/N
    sigma2_E = w_E.dot(V).dot(w_E)
    sigma_E = np.sqrt(sigma2_E)
    f_E = w_E.dot(f)
    # 最小方差组合
    w_C = V_inverse.dot(e)/e.T.dot(V_inverse).dot(e)
    sigma2_C = w_C.dot(V).dot(w_C)
    sigma_C = np.sqrt(sigma2_C)
    f_C = w_C.dot(f)
    # 夏普组合
    w_Q = V_inverse.dot(f)/f.T.dot(V_inverse).dot(e)
    sigma2_Q = w_Q.dot(V).dot(w_Q)
    sigma_Q = np.sqrt(sigma2_Q)
    f_Q = w_Q.dot(f)
    # 有效前沿曲线
    f_P = np.linspace(f_C,1.5*np.max(mu)) # 只取上半部分抛物线
    get_w_P = lambda fp: (f_Q-fp)/(f_Q-f_C)*w_C + (fp-f_C)/(f_Q-f_C)*w_Q
    w_P = np.array([get_w_P(fp) for fp in f_P])
    k = (sigma2_Q-sigma2_C)/(f_Q-f_C)**2
    sigma2_P = sigma2_C + k*(f_P-f_C)**2
    sigma_P = np.sqrt(sigma2_P)
    r_P = rf + w_P.dot(f)
    # 策略组合
    if strategy is not None:
        w_S,f_S,sigma_S = strategy(pred_ret,V)
    # 资本市场曲线CML
    s = np.linspace(0,0.2)
    CML = rf + f_Q/sigma_Q * s
    # 有效前沿曲线绘制
    plt.plot(sigma_P,r_P)
    plt.title('CML',fontsize=10)
    plt.xlabel('$\sigma$',fontsize=20)
    plt.ylabel('return of Portfolio',fontsize=20)
    #x_axis_low, x_axis_high = sigma_C-(sigma_P.max()-sigma_C)*0.1,sigma_P.max()
    x_axis_low, x_axis_high = 0,sigma_P.max()
    plt.xlim(x_axis_low, x_axis_high)
    # 绘制风险资产
    plt.plot(sigma,mu,'bo')
    x_axis_length = x_axis_high-x_axis_low
    text_margin_space = x_axis_length*0.03
    for i in range(N):
        plt.text(sigma[i]+text_margin_space,mu[i]-text_margin_space,'asset '+str(i+1),fontsize=10)
    # 绘制等权投资组合
    if show_E:
        plt.plot(sigma_E, rf+f_E,'ko')
        plt.text(sigma_E+text_margin_space,rf+f_E-text_margin_space,'E',fontsize=15)
    # 绘制策略组合
    if strategy:
        plt.plot(sigma_S, rf+f_S,'ko')
        plt.text(sigma_S+text_margin_space,rf+f_S-text_margin_space,'S',fontsize=15)
    # 绘制最小方差组合与夏普组合（市场组合），以及无风险资产
    plt.plot(sigma_C, rf+f_C,'go')
    plt.text(sigma_C+text_margin_space,rf+f_C-text_margin_space,'C',fontsize=15)
    plt.plot(sigma_Q, rf+f_Q,'ro')
    plt.text(sigma_Q-text_margin_space,rf+f_Q+text_margin_space,'Q',fontsize=15)
    plt.plot(0, rf,'yo')
    plt.text(0,rf+0.008,'$r_{f}$',fontsize=15)
    # 绘制CML
    plt.plot(s, CML, 'r-')
    plt.text(0.15,0.28,'CML',fontsize=15)
    if not is_subplot:
        plt.show()
plt.figure(figsize=(15,6))
plot_efficient_frontier(show_E=False)

在这里插入图片描述

CAPM资本市场定价模型

在均值方差分析框架里，至少需要两个输入，即预期收益率和协方差矩阵。先暂且不说预期收益率，对于有N个股票的协方差矩阵，我们需要估计 $\frac{N(N+1)}{2}$ 个变量（方差及协方差），
这个在实践中被认为是非常困难的任务，事实上，如果考虑到估计误差和动态特性，协方差矩阵的表现非常像量子力学里的随机矩阵，即大部分信息只集中在一两个特征值上面。因此，Sharpe、Tobin和Lintner
发展了一个结构更加简单的模型——CAPM。

CAPM把股票风险分解为系统风险和非系统风险：

\begin{align*}
r_i = r_f + \beta_i (r_m-r_f) + \epsilon_{i}
\end{align*}

其中：

\begin{align*}
\beta_i = \frac{cov(r_i,r_m)}{var(r_m)} = \frac{\rho_{i,M} \sigma_i}{\sigma_m}
\end{align*}

\begin{align*}
\epsilon_{i} \sim N(0, \theta_i^2)
\end{align*}

这里的 $\theta_i$ 经常被称为非系统风险。CAPM假设单个股票的系统性风险与非系统性是相互独立的，另外，它还假设不同股票间的非系统风险也是相互独立的。

CAPM下的协方差矩阵

可以从协方差的定义，很容易证明：

\begin{align*}
\Sigma &= \boldsymbol{\beta \beta^T} \sigma_m^2 + diag(\theta_1^2,\cdots ,\theta_N^2)\
&= \boldsymbol{\beta \beta^T} \sigma_m^2 + S\
&=
\begin{pmatrix}
\beta_1 \beta_1^T & \cdots & \beta_1 \beta_N^T \
\vdots & \ddots & \vdots \
\beta_N \beta_1^T & \cdots & \beta_N \beta_N^T
\end{pmatrix} \sigma_m^2 +
\begin{pmatrix}
\theta_1^2 & 0 & \boldsymbol{0} \
0 & \ddots & 0 \
\boldsymbol{0} & 0 & \theta_N^2
\end{pmatrix}
\end{align*}

对于组合权重为 $\boldsymbol{w}$ 的组合，组合beta就是股票beta的加权平均，即 $\beta_{p}=\boldsymbol{w^T \beta}$ 。

组合方差为：

\begin{align*}
\sigma_{p}^2 = \beta_{p}^2 \sigma_{m}^2 + \sum_{i=1}^N w_i^2 \theta_i^2
\end{align*}

正如我们所期望的，组合方差被分解为系统风险和非系统风险构成。

风险分散化

这里我们专门简单地讲一下为什么在CAPM的框架的，非系统性风险是可以被分散化的。为简单起见，我们假设所有股票都有相同的非系统风险（相同的方差），
那么一个等权重的股票组合的非系统性风险为 $\frac{\theta_0}{\sqrt{N}}$ 。如果单个股票非系统性风险为30%，那么对于100个股票的组合它的非系统性风险只有3%，
对于400个股票的组合非系统性风险只有1.5%。而系统性风险并不依赖于股票数量，仅仅是组合beta与市场风险的函数。不过，对于一只多空市场中性的股票组合，
我们可以构造一个多空市场中性的股票组合，它的组合beta为0，即没有市场风险。当然了，这个非常依赖我们对beta估计的准确性。

但如果我们每个证券组合存在相关性，那会怎么样呢？让我们假设一个股票组合证券两两相关性为 $\rho$ ，那么包含N个股票的组合风险为：

\begin{align*}
\sigma_{p} = \theta_0 \sqrt{\frac{1+\rho(N-1)}{N}}
\end{align*}

当N很大时，

\begin{align*}
\sigma_{p} \rightarrow \theta_0 \sqrt{\rho}
\end{align*}

所以，我们可以通过股票数量以及股票与组合间的相关性来降低组合总体风险。

CAPM实验

在下面的实验中，我们选取了平安银行和中证800的月频数据，然后计算它们的后验beta值，根据我们的计算得到了1.063的估计值。为了画出CAPM，我们还需要市场无风险利率，于是我取了shibor-1M的数据，
并在收益率的散点图上叠加了我们的CAPM曲线。从图中可以看到CAPM很完美的捕捉到了他们的关系，接着我们还对中证800和平安银行进行了线性回归从而得到了它们的回归系数，即1.067，R2为63%。我们可以看到，
我们的后验beta仍然落在了线性回归系数的95%置信区间内,(0.938,1.196)。

df = D.history_data(instruments=['000001.SZA', '000906.SHA'], start_date='2005-01-01', end_date='2017-12-31', fields=['close'])

# 重抽样还原至月度数据
resample_freq = 'M'
df_M = df.set_index('date')[['instrument','close']]\
                .groupby('instrument')\
                .apply(lambda df: df['close'].resample(resample_freq,how='last'))\
                .transpose()
ret_M = df_M.pct_change().dropna()

beta = np.cov(ret_M['000906.SHA'],ret_M['000001.SZA'])[0,1]/np.var(ret_M['000906.SHA'])

rf = 0.039/12
xs = np.linspace(-0.3,0.4,100)
ys = rf + beta*(xs-rf)

plt.plot(ret_M['000001.SZA'], ret_M['000906.SHA'],'o')
plt.plot(xs,ys,'r-')
plt.title('stock VS market')
plt.xlabel('return of market')
plt.ylabel('return of stock')
plt.show()

在这里插入图片描述

import statsmodels.api as sm
results = sm.OLS(ret_M['000001.SZA'],ret_M['000906.SHA']).fit()
print(results.summary())

在这里插入图片描述

SML证券市场线

这里再简单介绍下证券市场线。SML可以直接从我们对CAPM的定义得到，然后CAPM认为，在市场均衡的状态下，所有的股票都应该落在SML上，如果不是，那么将存在套利机会。
即我们可以卖空位于SML上面的股票，买入SML下面的股票，因为CAPM假设它们最终将回归到SML。

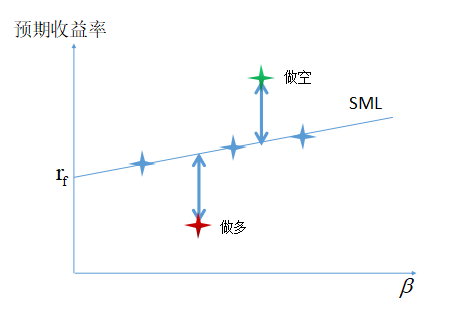
在下面的实验中，我们利用中证800指数的成分股数据，估计每个成分股的beta，并且在SML上展示了去年十月份的SML和个股的beta-收益对。我们可以看到，在这个时间片上，
股票个股的当月收益与beta似乎关联性并不强，而且SML似乎还有一点系统性地高估。为了展示一种分析方法，我们在SML上下设置了阈值区间，用以区分高估和低估的股票，这里的阈值
的设置没有一般规律，可以人为，也可以根据分位数。有兴趣的读者可以更近一步，把前后连续的两个月股票收益与SML的预测收益的离差作为一个事件，进行事件研究。

instruments = D.instruments()   #获取股票列表
df = D.history_data(instruments, start_date='2018-05-30', end_date='2018-05-30',
                    fields=['in_csi800'])   #获取一天历史数据
stock_list = list(df[df['in_csi800']== 1]['instrument']) #中证800指数成份股
df = D.history_data(instruments, start_date='2010-01-01', end_date='2017-12-31',
                    fields=['in_csi800','close'])
index_df = D.history_data('000906.SHA', start_date='2010-01-01', end_date='2017-12-31',
                    fields=['close']).set_index('date')[['close']]
# 重抽样还原至月度数据
resample_freq = 'M'
df_M = df.set_index('date')[['instrument','close']]\
                .groupby('instrument')\
                .apply(lambda df: df['close'].resample(resample_freq,how='last'))\
                .reset_index()\
                .set_index('date')
index_df_M = index_df.resample(resample_freq,how='last')#.pct_change().dropna()
                
def get_beta_ret(symbol, date):
    # 获取单股票beta值
    df1 = df_M[df_M['instrument']==symbol][['close']]
    df1 = df1.join(index_df_M,how='inner',lsuffix='_stock',rsuffix='_index')
    ret_df = df1.pct_change().dropna()
    beta = ret_df.cov().values[0,1]/np.var(ret_df.icol(1))
    if date in ret_df.index:
        ret = ret_df.ix[date]['close_stock']
    else:
        ret = None
    return beta,ret
beta_ret_dict = {symbol:get_beta_ret(symbol,'2017-10-31') for symbol in stock_list}
beta_ret = np.array([(beta,ret) for s,(beta,ret) in beta_ret_dict.items()])
recent_rm = index_df_M.pct_change().dropna().values[-3,0]

import seaborn as sns
sns.jointplot(x=beta_ret[:,0],y=beta_ret[:,1],kind='kde',xlim=(-.5,2),ylim=(-0.2,0.3))
plt.show()

threshold=0.1
betas = np.linspace(-3,3,100)
sml = rf + betas*(recent_rm-rf)
sml_u = sml+0.1
sml_d = sml-0.1
plt.plot(betas,sml,'-')
plt.plot(betas,sml_u,'r-')
plt.plot(betas,sml_d,'r-')
plt.plot(beta_ret[:,0], beta_ret[:,1],'o')
plt.xlim(-.5,2)
plt.ylim(-0.2,0.3)
plt.xlabel('beta')
plt.ylabel('return')
plt.title('SML on 2017-10')
plt.show()

在这里插入图片描述

APT套利定价模型

因子模型

\begin{align*}
r_i = a_{i} + b_{i1}f_1 + \cdots + b_{iK}f_K + \epsilon_{i}
\end{align*}

对于投资组合，我们有：

\begin{align*}
r_p = \boldsymbol{w^T a + w^T Bf + w^T \epsilon}
\end{align*}

我们的协方差矩阵：

\begin{align*}
\boldsymbol{\Sigma} = \boldsymbol{B \Sigma_I B^T + S}
\end{align*}

其中，B就是我们的暴露矩阵：

\begin{align*}
\boldsymbol{B} =
\begin{pmatrix}
b_11 & \cdots & b_1K \
\vdots & \ddots & \vdots \
b_N1 & \cdots & b_NK
\end{pmatrix}
= \boldsymbol{(b_1,\cdots,b_K)}
\end{align*}

$\Sigma_I$ 是因子的协方差矩阵，S则是股票的特异风险。

APT假设任何股票的收益都与一组因子线性相关， $b_{ij}$ 代表股票i的因子j的暴露程度或者敏感性， $\epsilon_{i}$ 代表股票i的特异收益率回报，其均值为0。它还假设股票的特异收益率在不同股票之间彼此不线性相关，
股票因子与因子之间不线性相关。

无套利均衡

无套利均衡是现代金融理论的重要概念，我们首先来定义套利机会：

1)不需要任何投入,自我融资(self-financing):

\begin{align*}
\boldsymbol{1^T w_A} = 0
\end{align*}

2)对所有因素风险完全免疫：

\begin{align*}
B^T \boldsymbol{w_A} = 0
\end{align*}

3)对所有非因素风险完全免疫:

\begin{align*}
\mathbb{E}[\boldsymbol{w_A^T \epsilon}] = 0
\end{align*}

4)当资产数目足够多时,期末可以获得无风险收益:

\begin{align*}
\mathbb{E}[r_A] &= \mathbb{E} [\boldsymbol{w_A^T a + w_A^T Bf + w_A^T \epsilon}] = \boldsymbol{w_A^T a}
\end{align*}

\begin{align*}
\lim_{n \to \infty} \mathbb{E}[r_A] &> 0
\end{align*}

无套利原则就是市场在均衡状态下不存在无套利机会。

APT与CAPM

CAPM和APT都是风险模型，然而它们之间存在着重要区别。首先，CAPM假设只有一个因子，即超额收益，对超额收益的暴露就是股票的beta。另外一方面，APT则要通用的多，但在APT模型中，
它并没有告诉我们存在哪些因子以及因子数量，并且APT没有告诉我们怎么具体得定义和衡量股票对因子的暴露。APT在定义上的宽泛引发了一系列的问题，其中一个就是使得这个理论难以在实践中被检验。
同时，它的灵活性也提供了许多方法和思路去探究股票收益的生成过程。因此也引发了很多研究和一些商业应用，其中比较有名的就是BARRA风险结构模型。

因子的定义

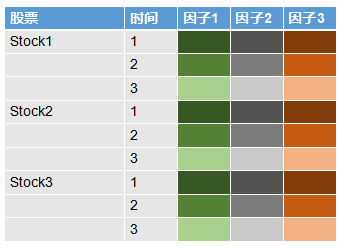
这里着重介绍下，我觉得大家好像特别容易把因子和特征搞混。在APT的标准定义里，每个股票的因子 $f_k$ 是相同的一组变量，注意这里并不是 $f_{ik}$ ，i代表股票，k代表第k个因子。我画了一个图，来帮助大家理解。
大家可以看到，左边的两列分别代表股票和时间，后三列代表的是三个不同的因子，图中因子下面的单元格的不同颜色代表不同值。不难发现，图中每个股票每个时间下面各个因子的颜色（值）是一样的，也就是说因子变量在
不同股票间是共享的，每个股票的因子数据就是所有股票的共同因子数据，不过是在不同股票间重复而已。作为对比，我还列了一个一般意义上表示特征的表格，大家可以发现在特征表格中所有的值在一般意义上都是不同的。

这里给出了一些挖掘潜在因子的先验指南：

它们能够捕捉价格的非预期变动
它们应该表示无法通过分散化来抵消的影响因素，所以更可能是宏观经济因素，而不是股票或公司特有的因素
能够获取及时且准确的信息
它们之间的关系应该有经济学理论解释

下面我们给出了一些建议列表：

通胀率
油价
汇率
商品、贵金属
股票指数
短期利率

所以在APT的框架逻辑是，通过因子建模和挖掘，捕捉股票的系统性特性，而非系统性特性通过组合分散化的技术可以消除。在实践中，如果我们需要捕捉股票的特异因素，就再加入股票的特异特征就可以了，比如市盈率、市净率。
只不过在传统统计建模视角，每个股票的非特异因素可能是不同的，或者说对不同的特异变量的t检验的显著性是不一样的，那么作为单个股票的收益预测模型，似乎没有必要加入不显著的变量，然后在一只股票上的不显著变量
在另一只股票上可能是统计显著的。而且在实践中每个股票都有不同的收益预测模型似乎也是缺少实践性的。但是在统计学习或者机器学习视角，我们关注的是特征，不太关注特征本身的统计性质，机器学习能够比传统统计技术获得
更高的泛化能力和更好的预测性能，相比牺牲了一些模型的诠释能力，而且机器学习更能够捕捉特征的非线性特征。

Fama-French 的三因子模型

\begin{align*}
E \lbrack r(t)-r_f(t) \rbrack = \alpha + \beta \centerdot E \lbrack r_B(t) \rbrack +
s \centerdot E \lbrack SMB(t) \rbrack +h \centerdot E \lbrack HML(t) \rbrack
\end{align*}

下面我们演示如何得到Fama-French的三因子模型，分别是市场因子，规模因子和价值因子。规模因子我们用中证100和中证500的差，
价值因子我们用市净率排名前25%的股票市净率之和减去排名后25%的股票市净率之和。然后我们对这些因子分别做了规范化和极值处理。
最后我们抽了1000多只数据全的股票做线性回归，得到R2接近30%的三因子模型。

这里只做演示，因子的定义及因子的处理或许有更好的方式，也没展示训练与测试阶段模型的性能对比，同时我们用的是截面数据，在实际
收益预测时，当期因子是未知的，我们也没有就这个问题展开（思路是构建专门的因子预测模型，或者因子的一致预期，或者用滞后一阶的历史数据
作为因子）。后续因子检验和因子建模的课程会详细展开这些问题，读者有不同想法可以在帖子留言讨论。

start_date = '2006-01-01'  
end_date = '2017-12-31'

rf = 0.039/12
benchmark = '000906.SHA'
instruments = D.instruments(start_date, end_date)
df = D.history_data(instruments, start_date, end_date,fields=['close','pb_lf','amount'])
index_df = D.history_data(instruments=[benchmark,'000903.SHA', '000905.SHA'], 
                          start_date=start_date, end_date=end_date, fields=['close'])

# 重抽样还原月指数数据
resample_freq = 'M'
index_resampled = index_df.pivot(index='date', columns='instrument', values='close')\
                    .resample(resample_freq,how='last')\
                    .dropna()

# 重抽样还原股票相关数据
df_resampled = pd.DataFrame(
            {'pb_lf':df.set_index('date')[['instrument','pb_lf']]\
                .groupby('instrument')\
                .apply(lambda df: df['pb_lf'].resample(resample_freq,how='last')),
            'close':df.set_index('date')[['instrument','close']]\
                .groupby('instrument')\
                .apply(lambda df: df['close'].resample(resample_freq,how='last')),
            'amount':df.set_index('date')[['instrument','amount']]\
                .groupby('instrument')\
                .apply(lambda df: df['amount'].resample(resample_freq,how='last'))})

df_resampled = df_resampled.reset_index('instrument')
        
        
def get_SMB(index_w_df):
    # 中证100
    zz100 = index_w_df['000903.SHA']
    # 中证500
    zz500 = index_w_df['000906.SHA']
    SMB = (zz100 - zz500)
    return pd.DataFrame({'SMB':SMB})

def get_HML(df, resample_freq=resample_freq):
    def get_group_HML(df):
        grouped_df = df[(df['amount'] > 0)&((df['pb_lf'] > 0))].sort_values('pb_lf')
        grouped_df30 = np.percentile(grouped_df['pb_lf'],30) #低市净率
        grouped_df70 = np.percentile(grouped_df['pb_lf'],70) #高市净率
        L = grouped_df[grouped_df['pb_lf'] <= grouped_df30]['pb_lf'].sum()
        H = grouped_df[grouped_df['pb_lf'] > grouped_df70]['pb_lf'].sum()
        return H - L
    HML = df.reset_index().groupby('date').apply(lambda df: get_group_HML(df)).resample(resample_freq,how='last')
    return HML

factor_df = index_resampled[['000906.SHA']].pct_change().dropna()
factor_df['HML'] = get_HML(df)
factor_df['SMB'] = get_SMB(index_resampled)
factor_df = factor_df.rename(columns={'000906.SHA':'BER'})

## 极值处理
for factor in ['BER', 'SMB', 'HML']:
    p_975 = np.percentile(factor_df[factor], 97.5)
    p_025 = np.percentile(factor_df[factor], 2.5)
    factor_df[factor][factor_df[factor] > p_975] = p_975
    factor_df[factor][factor_df[factor] < p_025] = p_025
    
## 标准化
for factor in ['HML', 'SMB']:
    factor_df[factor] = (factor_df[factor] - factor_df[factor].mean()) / factor_df[factor].std()

## 获取标注数据
df_resampled = df_resampled[~df_resampled['pb_lf'].isnull()]
stock_ret_df = df_resampled.reset_index()\
    .groupby('instrument')\
    .apply(lambda df: df.set_index('date')['close'].pct_change().dropna())\
    .reset_index()\
    .set_index('date')\
    .rename(columns={'close':'ret_M'})\
    .pivot(columns='instrument',values='ret_M')
    
# 为演示目的，抽取没有NaN的股票
subset_ret_df = stock_ret_df.transpose()[(stock_ret_df.isnull().sum() == 0)].transpose()

# 三因子预测模型
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
reg.fit(factor_df, subset_ret_df)
reg.score(factor_df, subset_ret_df)

我们还给出了各个股票三个系数的分布情况

plt.figure(figsize=(20,5))
plt.subplot(1,3,1)
plt.hist(reg.coef_[:,0])
plt.title("coef of market")

plt.subplot(1,3,2)
plt.hist(reg.coef_[:,1])
plt.title("coef of SMB")

plt.subplot(1,3,3)
plt.hist(reg.coef_[:,2])
plt.title("coef of HML")
plt.show()

在这里插入图片描述

总结

最优夏普组合是CML与有效前沿曲线相切，是有效前沿上夏普率最大的风险组合
有效市场假说认为，最优夏普组合就是市场组合
CML是由无风险资产和市场组合（风险资产）的加权组合，投资者应该在CML上选取投资组合
CAPM认为股票收益尤市场风险和特异风险组成，beta衡量股票超额风险的暴露程度，市场组合的暴露程度为1
SML是在CAPM下衡量股票均衡定价的一个工具，应该卖空SML上方的股票，买入SML下方的股票
APT提供了一个股票收益多因子模型框架，是比CAPM更一般的模型
APT灵活度很高，在实践中很难对模型进行检验
因子应该代表股票的共同因素，而不是特异因素

开放性问题

1.在MPT框架下，CML是夏普比率最高的投资组合，如何解释一些共同基金、私募拥有超过市场组合的夏普比率？

2.夏普比率的计算在样本选择、抽样方式以及样本分布上有什么关系和规律？

3.我们通常得用夏普比率来衡量投资组合真的能真实反映投资绩效和基金经理的能力么？

源码地址：《Alpha系列——从MPT到APT》

本文由BigQuant人工智能量化投资平台原创推出，版权归BigQuant所有，转载请注明出处。

posted @ 2019-01-12 10:51 BigQuant量化阅读(19) 评论(0) 编辑收藏举报来源

刷新页面返回顶部

bigquant

Alpha系列——从MPT到APT

从MPT到APT

夏普组合与CML

风险溢价

CAPM资本市场定价模型

CAPM下的协方差矩阵

风险分散化

CAPM实验

SML证券市场线

APT套利定价模型

因子模型

无套利均衡

APT与CAPM

因子的定义

Fama-French 的三因子模型

总结

开放性问题

1.在MPT框架下，CML是夏普比率最高的投资组合，如何解释一些共同基金、私募拥有超过市场组合的夏普比率？

2.夏普比率的计算在样本选择、抽样方式以及样本分布上有什么关系和规律？

3.我们通常得用夏普比率来衡量投资组合真的能真实反映投资绩效和基金经理的能力么？

源码地址：《Alpha系列——从MPT到APT》

公告