基于一维卷积神经网络模型的AI量化智能选股策略
这是早前BigQuant专题研究:基于卷积神经网络CNN的深度学习因子选股模型。卷积神经网络(Convolutional Neural Network, CNN),是计算机视觉研究和应用领域中最具影响力的模型之一。同样,如果将时间看作一个空间维度,类似于二维图像的高度或宽度,CNN也可以对时间序列处理产生令人惊喜的效果。本文首先大致介绍了CNN的原理,然后详细解释了一维CNN模型如何进行应用于时间序列并进行特征选取,最后以一个实例展示一维CNN模型在因子选股方面的应用。
目录
1.CNN原理介绍
1.1 反向传播算法
1.2 CNN图像识别原理
2.一维CNN在时间序列中的应用
2.1 一维卷积
2.2 一维池化
3.实例:CNN模型选股
1.CNN原理介绍
1.1 反向传播算法
反向传播(Backpropagation,缩写为BP)是“误差反向传播”的简称,是一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见方法。该方法对网络中所有权重计算损失函数的梯度,这个梯度会反馈给最优化方法,用来更新权值以最小化损失函数。 一句话解释:前向传递输入信号直至输出产生误差,反向传播误差信息更新权重矩阵。 以没有隐层的神经网络为例,如逻辑回归,其中小黄帽代表输出层节点,左侧接受输入信号,右侧产生输出结果,小蓝猫则代表了误差,指导参数往更优的方向调整。由于小蓝猫可以直接将误差反馈给小黄帽,同时只有一个参数矩阵和小黄帽直接相连,所以可以直接通过误差进行参数优化(实线),迭代几轮,误差会降低到最小。
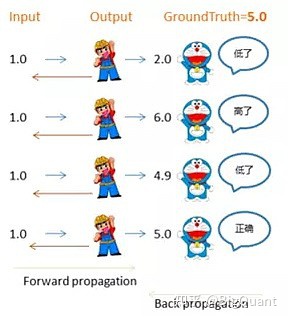
图1:无隐层反向传播算法示意 图1:无隐层反向传播算法示意
1.2 CNN图像识别原理
卷积神经网络的结构模仿了眼睛的视觉神经的工作原理。对于眼睛来说,大量的视觉神经分工协作,各自负责一小部分区域的视觉图像,再将图像的各种局部特征抽象组合到高层的视觉概念,传送到大脑使人类产生视觉。卷积神经网络也是类似,它包含了至少一层卷积层,由多个卷积核对图像的局部区域进行特征提取,最后进行合成。 以经典的LeNet-5模型为例:
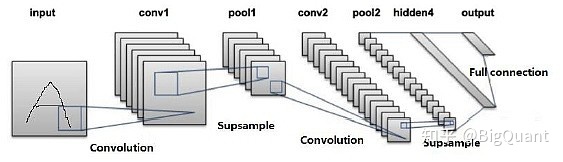
图2:LeNet−5卷积神经网络模型 原始输入数据(图1中的input)为二维图像,横轴和纵轴分别是图像的高度和宽度的像素点,为了识别该图像,模型依次完成以下步骤: 第一层卷积层(图1中的conv1)进行卷积运算。该层由若干卷积核组成,每个卷积核的参数都是通过反向传播算法优化得到的。卷积核的目的是通过扫描整张图片提取不同特征,第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级。在卷积层之后都会使用非线性激活函数(如RELU,tanh 等)对特征进行非线性变换。第一层池化层(图1中的pool1)进行池化运算。通常在卷积层之后会得到维度很大的特征,池化层可以非常有效地缩小参数矩阵的尺寸,从而减少最后全连层中的参数数量。使用池化层既可以加快计算速度也有防止过拟合的作用。一般池化层将特征切成几个区域,取其最大值或平均值,得到新的、维度较小的特征。池化层其实是在对具有高维特征的图片进行特征降维(subsample)。第二层卷积层和第二层池化层(图1中的conv2 和pool2) 进行进一步的特征提取和特征降维,得到更加高层和抽象的特征。全连接层(图1中的hidden4 和full connection) 把卷积核池化得到的特征展平为一维特征,用来进行最后的训练和预测。 总结而言,卷积层进行特征提取,池化层进行特征降维以防止过拟合。CNN通过上述过程实现了图像识别:

图3:CNN图像识别
通过第一层卷积识别边缘等低级特征,池化后通过第二层卷积识别眼睛、鼻子等小区域器官这样的中级特征,池化,最后通过第三层卷积识别整个面容这样的高级特征,最后通过全连接层整合,识别出最终的图像。
2.一维CNN在时间序列中的应用
CNN最主要应用于计算机视觉领域,通过卷积运算,从二维图像中提取特征,最终实现优秀的图像识别功能。对于这样一种优秀的算法,我们自然会思考如何将其运用到时间序列分析中。很容易想到,有两种思路: 将一维的时间序列二维化。考虑历史截面期,将每个样本的特征数据组织成二维形式,尝试构建“特征图片”。如总共有3000个样本,每个样本有10个特征,那就考虑5个截面期,每个样本整合5个截面得到一张“特征图片”,用时间数据作为图片标签。如此,可以得到3000个带时间特征的图片,然后运用二维CNN处理。这种方法的具体实现可参见华泰证券的研报《人工智能选股之卷积神经网络》探索一维CNN在时间序列上的运用。本篇研究就是基于这个思路。如果将时间理解为图像的长或者宽,其他特征理解为一个维度,那么就可以用一维CNN进行处理。
2.1 一维卷积
一维卷积,也就是从序列中按照一定大小的窗口提取局部一维序列段(即子序列),然后与一个权重做点积,然后输出为新序列上的一个部分。以大小为5的时间窗口为例:
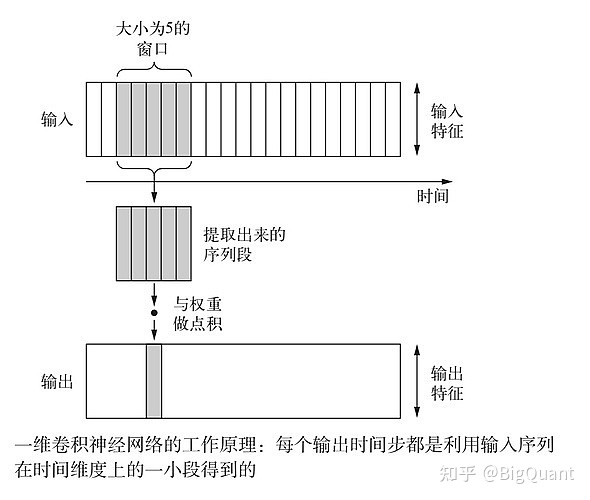
图4:一维CNN的一层卷积示意
2.2 一维池化
同二维池化一样,一维池化的目的也是为了对卷积的结果“模糊化”,归纳局部区域内的统计特征,并且通过降维避免过拟合。一维池化是从输入中提取一维序列段(即子序列), 然后输出其最大值(最大池化)或平均值(平均池化),降低一维输入的长度(子采样)。
3.实例:CNN模型选股
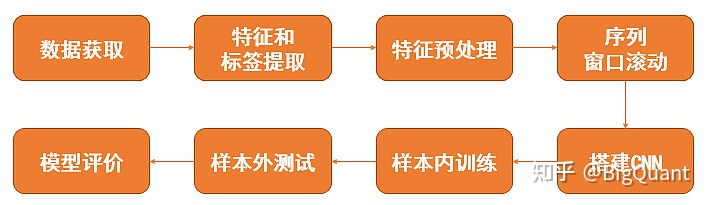
图5:CNN智能选股策略 如图5所示,一维CNN选股策略构建包含下列步骤:
获取数据 :A股所有股票。
特征和标签提取 :计算7个因子作为样本特征;计算第2日的个股收益,极值处理后分成20类作为标签。
特征预处理 :进行缺失值处理;去掉特征异常的股票,比如某个特征值高于99.5%或低于0.5%的;标准化处理,去除特征量纲/数量级差异的影响。
序列窗口滚动 :窗口大小设置为5,滚动切割。
搭建CNN模型 :构建一个简单的两层一维卷积神经网络预测股票价格。
模型训练与预测 :使用CNN模型进行训练和预测;可以尝试多种激活函数,策略默认为relu。
策略回测 :利用2010到2014年数据进行训练,预测2015到2017年的股票表现。每日买入预测排名最靠前的20只股票,至少持有2日,同时淘汰排名靠后的股票。具体而言,预测排名越靠前,分配到的资金越多且最大资金占用比例不超过20%;初始5日平均分配资金,之后,尽量使用剩余资金(这里设置最多用等量的1.5倍)。
模型评价 :查看模型回测结果。 一维CNN模型的参数如下:
输入数据:输入是形状为 (samples, time, features)的三维张量,并返回类似形状的三维张量。卷积窗口是时间轴上的一维窗口(时间轴是输入张量的第二个轴)。7个因子,时间窗口为5,因此输入7*5的一个矩阵。
卷积层:2层一维卷积层(Conv1D层),每层包含20 个卷积核。激活函数采用relu。同时选择“valid”参数,只进行有效卷积,对边界数据不处理。卷积核权重使用glorot_uniform初始化方法,偏置向量使用Zeros初始化方法。
池化层:2层池化层。
全连接层:激活函数linear。权重使用glorot_uniform初始化方法,偏置向量使用Zeros初始化方法。
训练次数率:epochs值为5,共训练5轮,以mae作为评估指标。
优化器和:RMSProp。损失函数:均方误差MSE。 预测结果如下:
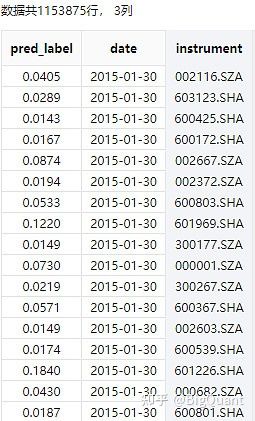
图6:CNN模型预测结果
回测结果如下:
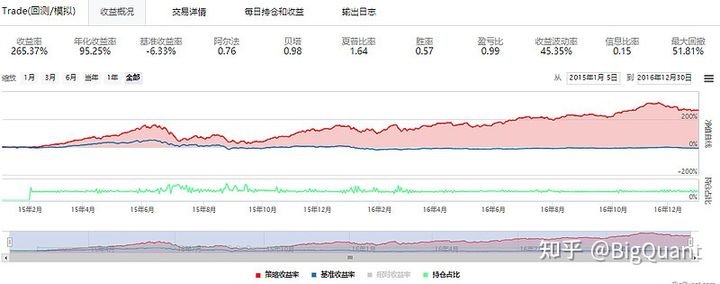
图7:CNN模型回测结果
可以看到,CNN的回测结果还是非常惊喜的,相比于基准收益有着非常突出的表现。所以,我们认为将CNN卷积神经网络应用于资本市场因子选股是很有前景的。在本次的策略中,我们运用了两层的一维CNN模型,具体的卷积层数、模型参数有非常大的调整空间,欢迎大家尝试。 策略克隆:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号