【机器学习】BP神经网络实现手写数字识别
最近用python写了一个实现手写数字识别的BP神经网络,BP的推导到处都是,但是一动手才知道,会理论推导跟实现它是两回事。关于BP神经网络的实现网上有一些代码,可惜或多或少都有各种问题,在下手写了一份,连带着一些关于性能的分析也写在下面,希望对大家有所帮助。
加一些简单的说明,算不得理论推导,严格的理论推导还是要去看别的博客或书。
BP神经网络是一个有监督学习模型,是神经网络类算法中非常重要和典型的算法,三层神经网络的基本结构如下:
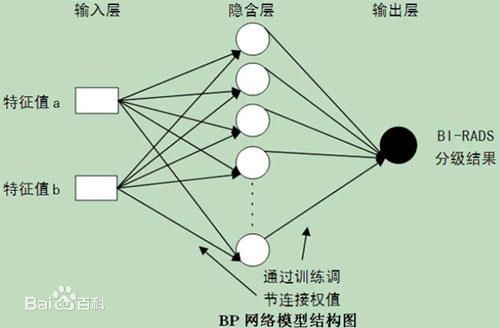
这是最简单的BP神经网络结构,其运行机理是,一个特征向量的各个分量按不同权重加权,再加一个常数项偏置,生成隐层各节点的值。隐层节点的值经过一个激活函数激活后,获得隐层激活值,隐层激活值仿照输入层到隐层的过程,加权再加偏置,获得输出层值,通过一个激活函数得到最后的输出。
上面的过程称为前向过程,是信息的流动过程。各层之间采用全连接方式,权向量初始化为随机向量,激活函数可使用值域为(0,1)的sigmoid函数,也可使用值域为(-1,1)的tanh函数,两个函数的求导都很方便。
BP神经网络的核心数据是权向量,经过初始化后,需要在训练数据的作用下一次次迭代更新权向量,直到权向量能够正确表达输入输出的映射关系为止。
权向量的更新是根据预测输出与真值的差来更新的,前面说过BP神经网络是一个有监督学习模型,对于一个特征向量,可以通过神经网络前向过程得到一个预测输出,而该特征向量的label又是已知的,二者之差就能表达预测与真实的偏差情况。这就是后向过程,后向过程是误差流动的过程。抛开具体的理论推导不谈,从编程来说,权值更新的后向过程分为两步。
第一步,为每个神经元计算偏差δ,δ是从后向前计算的,故称之为后向算法。对输出层来说,偏差是 act(预测值-真值),act为激活函数。对隐层而言,需要从输出层开始,逐层通过权值计算得到。确切的说,例如对上面的单隐层神经网络而言,隐层各神经元的δ就是输出层δ乘以对应的权值,如果输出层有多个神经元,则是各输出层神经元δ按连接的权值加权生成隐层的神经元δ。
第二步,更新权值,w=w+η*δ*v 其中η是学习率,是常数。v是要更新的权值输入端的数值,δ是要更新的权值输出端的数值。例如更新隐层第一个神经元到输出层的权值,则δ是第一步计算得到的输出层数值,v是该权值输入端的值,即隐层第一个神经元的激活值。同理如果更新输入层第一个单元到隐层第一个单元的权值,δ就是隐层第一个单元的值,而v是输入层第一个单元的值。
偏置可以看作“1”对各神经元加权产生的向量,因而其更新方式相当于v=1的更新,不再赘述。在编程中可以将1强行加入各层输入向量的末尾,从而不单独进行偏置更新,也可以不这样做,单独把偏置抽出来更新。下面的算法采用的是第二种方法。
OK,简单解释完了,下面介绍这个程序。
一、数据库
程序使用的数据库是mnist手写数字数据库,这个数据库我有两个版本,一个是别人做好的.mat格式,训练数据有60000条,每条是一个784维的向量,是一张28*28图片按从上到下从左到右向量化后的结果,60000条数据是随机的。测试数据有10000条吧好像,记不太清了。另一个版本是图片版的,按0~9把训练集和测试集分为10个文件夹,两个版本各有用处,后面会说到,本程序用的是第一个版本。第二个版本比较大,不好上传,第一个版本在https://github.com/MoyanZitto/BPNetwork/里可以找到。
二、程序结构
程序分四个部分,第一个部分数据读取,第二个部分是神经网络的配置,第三部分是神经网络的训练,第四部分是神经网络的测试,最后还有个神经网络的保存,保存效果很差,大概没有做优化的缘故,不过仔细按保存方法设置程序还是能读出来的,只关心神经网络的实现的同学无视就好。
三、代码和注释
1 # -*- coding: utf-8 -*- 2 #本程序由UESTC的BigMoyan完成,并供所有人免费参考学习,但任何对本程序的使用必须包含这条声明 3 import math 4 import numpy as np 5 import scipy.io as sio 6 7 8 # 读入数据 9 ################################################################################################ 10 print "输入样本文件名(需放在程序目录下)" 11 filename = 'mnist_train.mat' # raw_input() # 换成raw_input()可自由输入文件名 12 sample = sio.loadmat(filename) 13 sample = sample["mnist_train"] 14 sample /= 256.0 # 特征向量归一化 15 16 print "输入标签文件名(需放在程序目录下)" 17 filename = 'mnist_train_labels.mat' # raw_input() # 换成raw_input()可自由输入文件名 18 label = sio.loadmat(filename) 19 label = label["mnist_train_labels"] 20 21 ################################################################################################## 22 23 24 # 神经网络配置 25 ################################################################################################## 26 samp_num = len(sample) # 样本总数 27 inp_num = len(sample[0]) # 输入层节点数 28 out_num = 10 # 输出节点数 29 hid_num = 9 # 隐层节点数(经验公式) 30 w1 = 0.2*np.random.random((inp_num, hid_num))- 0.1 # 初始化输入层权矩阵 31 w2 = 0.2*np.random.random((hid_num, out_num))- 0.1 # 初始化隐层权矩阵 32 hid_offset = np.zeros(hid_num) # 隐层偏置向量 33 out_offset = np.zeros(out_num) # 输出层偏置向量 34 inp_lrate = 0.3 # 输入层权值学习率 35 hid_lrate = 0.3 # 隐层学权值习率 36 err_th = 0.01 # 学习误差门限 37 38 39 ################################################################################################### 40 41 # 必要函数定义 42 ################################################################################################### 43 def get_act(x): 44 act_vec = [] 45 for i in x: 46 act_vec.append(1/(1+math.exp(-i))) 47 act_vec = np.array(act_vec) 48 return act_vec 49 50 def get_err(e): 51 return 0.5*np.dot(e,e) 52 53 54 ################################################################################################### 55 56 # 训练——可使用err_th与get_err() 配合,提前结束训练过程 57 ################################################################################################### 58 59 for count in range(0, samp_num): 60 print count 61 t_label = np.zeros(out_num) 62 t_label[label[count]] = 1 63 #前向过程 64 hid_value = np.dot(sample[count], w1) + hid_offset # 隐层值 65 hid_act = get_act(hid_value) # 隐层激活值 66 out_value = np.dot(hid_act, w2) + out_offset # 输出层值 67 out_act = get_act(out_value) # 输出层激活值 68 69 #后向过程 70 e = t_label - out_act # 输出值与真值间的误差 71 out_delta = e * out_act * (1-out_act) # 输出层delta计算 72 hid_delta = hid_act * (1-hid_act) * np.dot(w2, out_delta) # 隐层delta计算 73 for i in range(0, out_num): 74 w2[:,i] += hid_lrate * out_delta[i] * hid_act # 更新隐层到输出层权向量 75 for i in range(0, hid_num): 76 w1[:,i] += inp_lrate * hid_delta[i] * sample[count] # 更新输出层到隐层的权向量 77 78 out_offset += hid_lrate * out_delta # 输出层偏置更新 79 hid_offset += inp_lrate * hid_delta 80 81 ################################################################################################### 82 83 # 测试网络 84 ################################################################################################### 85 filename = 'mnist_test.mat' # raw_input() # 换成raw_input()可自由输入文件名 86 test = sio.loadmat(filename) 87 test_s = test["mnist_test"] 88 test_s /= 256.0 89 90 filename = 'mnist_test_labels.mat' # raw_input() # 换成raw_input()可自由输入文件名 91 testlabel = sio.loadmat(filename) 92 test_l = testlabel["mnist_test_labels"] 93 right = np.zeros(10) 94 numbers = np.zeros(10) 95 # 以上读入测试数据 96 # 统计测试数据中各个数字的数目 97 for i in test_l: 98 numbers[i] += 1 99 100 for count in range(len(test_s)): 101 hid_value = np.dot(test_s[count], w1) + hid_offset # 隐层值 102 hid_act = get_act(hid_value) # 隐层激活值 103 out_value = np.dot(hid_act, w2) + out_offset # 输出层值 104 out_act = get_act(out_value) # 输出层激活值 105 if np.argmax(out_act) == test_l[count]: 106 right[test_l[count]] += 1 107 print right 108 print numbers 109 result = right/numbers 110 sum = right.sum() 111 print result 112 print sum/len(test_s) 113 ################################################################################################### 114 # 输出网络 115 ################################################################################################### 116 Network = open("MyNetWork", 'w') 117 Network.write(str(inp_num)) 118 Network.write('\n') 119 Network.write(str(hid_num)) 120 Network.write('\n') 121 Network.write(str(out_num)) 122 Network.write('\n') 123 for i in w1: 124 for j in i: 125 Network.write(str(j)) 126 Network.write(' ') 127 Network.write('\n') 128 Network.write('\n') 129 130 for i in w2: 131 for j in i: 132 Network.write(str(j)) 133 Network.write(' ') 134 Network.write('\n') 135 Network.close()
四、几点分析和说明
1.基本上只要有numpy和scipy,把github上的数据拷下来和程序放在一个文件夹里,就可以运行了。为了处理其他数据,应该把数据读入部分注释掉的raw_input()取消注释,程序运行时手动输入文件名。
2.关于输入特征向量,简单的把像素点的值归一化以后作为输入的特征向量理论上是可行的,因为真正有用的信息如果是这个特征向量的一个子集的话,训练过程中网络会自动把这些有用的信息选出来(通过增大权重),然而事实上无用信息,也会对结果造成负面影响,因而各位可以自己做一个特征提取的程序优化特征,有助于提高判断准确率。我懒,就这么用吧。
3.关于隐层的层数和神经元节点数,隐层的层数这里只有一层,因为理论上三层神经网络可以完成任意多种的分类,实际上隐层的数目在1~2层为好,不要太多。隐层的神经元节点数是个神奇的存在,目前没有任何理论能给出最佳节点数,只有经验公式可用。这里用的经验公式是sqrt(输入节点数+输出节点数)+0~9之间的常数,也可以用log2(输入节点数),具体多少需要反复验证,这个经验公式还是有点靠谱的,至少数量级上没有太大问题。如果隐层节点数太多,程序一定会过拟合,正确率一定惨不忍睹(我曾经10%,相当于瞎猜)。
4.关于训练方法,本程序用的是在线学习,即来一个样本更新一次,这种方式的优点是更容易收敛的好,避免收敛到局部最优点上去。
5.学习率、误差门限和最大迭代次数,学习率决定了梯度下降时每步的步长,会影响收敛速度,同时学习率太大容易扯着蛋(划掉),容易在山谷处来回倒腾hit不到谷底,学习率太大容易掉进局部的小坑里出不来,也是一个需要仔细设置的量。误差门限本程序虽然设置了但是没有使用,最大迭代次数我连设置都没设置,这两个量的作用主要在提前结束训练,而因为我的程序连训练带测试跑一次也就20s,所以懒得提前结束训练。但在应用时还是应该设置一下的。
6.这个程序是最简单的BP神经网络,没有使用所谓动量因子加速收敛,也没有乱七八糟别的玩意,基本上就是原生的BP神经网络算法,代码注释都是中文而且写的很全,仔细阅读应该理解上并不难。推荐使用pycharm阅读和修改。
7.补充一下实验结果,表格行为不同的隐层神经元数目,列为不同学习率,内容都是overall的正确率,可见最佳神经元个数在15附近,最佳学习率在0.2附近。
以上,有问题欢迎评论提问。



