寻找“最好”(8)——牛顿法
牛顿是近代科学的先驱,智商290,碾压无数学霸,一个苹果都能砸出万有引力定律。
在力学上,牛顿阐明了动量和角动量守恒的原理,提出牛顿三大运动定律,它们和万有引力定律奠定了此后三个世纪里物理世界的科学观点,并成为无数中学生的噩梦。牛顿他通过论证开普勒行星运动定律与他的引力理论间的一致性,展示了地面物体与天体的运动都遵循着相同的自然定律;为太阳中心说提供了强有力的理论支持,并推动了科学革命。
在天文学上,牛顿创制了反射望远镜。他还用万有引力原理说明潮汐的各种现象,指出潮汐的大小不但同月球的位相有关,而且同太阳的方位有关。牛顿预言地球不是正球体。
在哲学上,牛顿的哲学思想基本属于自发的唯物主义,他承认时间、空间的客观存在。如同历史上一切伟大人物一样,牛顿虽然对人类作出了巨大的贡献,但他也不能不受时代的限制。例如,他把时间、空间看作是同运动着的物质相脱离的东西,提出了所谓绝对时间和绝对空间的概念;他对那些暂时无法解释的自然现象归结为上帝的安排,提出一切行星都是在某种外来的“第一推动力”作用下才开始运动的说法。
在经济学上,牛顿提出金本位制度。这是一种以黄金为本位币的货币制度,当不同国家使用金本位时,国家之间的汇率由它们各自货币的含金量之比——金平价来决定。
在数学上,我们已经见识过牛顿的微积分,他与莱布尼茨共同分享了微积分学的荣誉,尽管哥俩为谁的功劳大掐过架。
此外,牛顿还提出了著名的牛顿法(Newton's method)也叫牛顿迭代法,它是牛顿在17世纪提出的一种在实数域和复数域上近似求解值的方法。
牛顿法
先来看如何用牛顿迭代法求解5的平方根。
首先令f(x)= x2 – 5,这是标准步骤,取得一个新函数;再令该函数为0,这样原问题就可以看作是解方程x2 – 5 = 0。f(x)是一个抛物线:
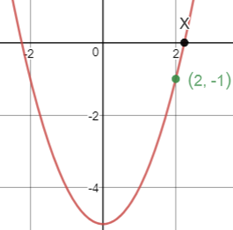
抛物线与x轴正方向的交点x就是方程的解,它比2稍大一点。
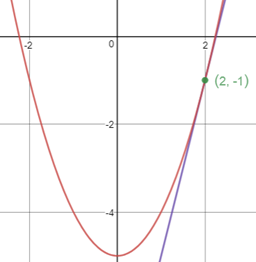
现在在x = 2的点(2, -1)处对f(x)做切线,切线方程是y = kx + b,斜率k是f(x)在x = 2处的导数:

将(2, -1)代入切线后得到截距b= -9:
设f(x)与x轴正半轴的交点是x,切点是x0,切线与x轴的交点是x1,x1在x的右侧:
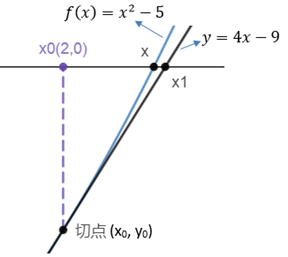
由于x1贴近x,所以只要求得x1就能近似地求出x。求解x1的方法之一是找出过x0的切线,之后计算切线与x轴的交点。设切线的斜率是k,根据斜率的公式:
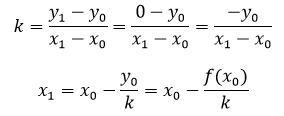
过x0的切线的斜率正式f(x)在x0处导数的定义,因此:
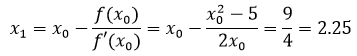
这样一来就找到了x的近似解x1。然而x1还没达到标准,我们还想更贴近真实值一点,这次选取更进接近x的(x1, f(x1))做切点,新切点的切线与x轴的交点x2将比原来的x1更贴近x:
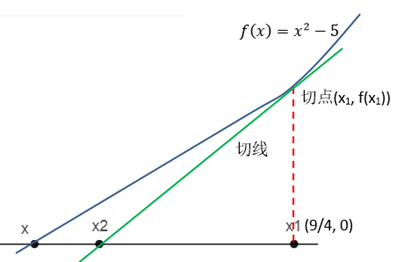
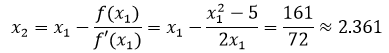
计算器上计算根号5的结果是2.236067,x2的值已经相当接近。
重复上面步骤,每一次迭代的结果都将更接近真实值:
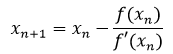
这就是牛顿迭代法的公式。
牛顿法的注意事项
牛顿迭代法几乎可以求解所有方程,但它仍然有一些限制。
在使用牛顿迭代法时,需要选取x0作为迭代基数,x0如何选取呢?一句参考是:x0要在x附近,它是一个较为解接近真实解的值,这要凭经验和感觉了,没有什么太好的办法。
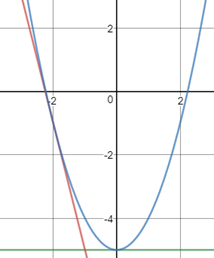
实际上,如果x0和x的差距过大,可能会得到一个没谱的解。以计算5的平方根为例,如果选择x0= -2,结果将偏向于-2.236067;如果选择x0=0,则f’(0)=0,没法继续迭代:
设第n次迭代的误差是En=|x-xn|,那么需要满足En+1<En。如果选择和计算都正确,误差缩小的速度将非常快。
从泰勒公式看牛顿法
泰勒展开式是一种计算近似值的方法,是一个用函数某点的信息描述在该点附近取值的公式,这就与牛顿法有些相似了。
把f(x)在x0的某邻域内展开成泰勒级数:
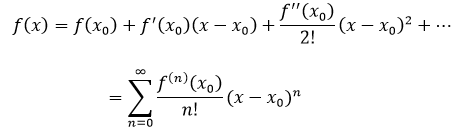
进一步得到:

反复迭代就得到了牛顿法的公式:
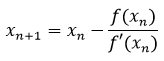
解方程2cosx = 3x
先作图,画出y = 2cosx和y = 3x的曲线:

两条曲线相交于一点,方程存在唯一解。根据牛顿法,先设置f(x):
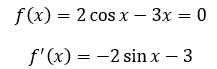
两条曲线交点的位置似乎是π/6附近,所以选择π/6作为x0,根据牛顿迭代法:
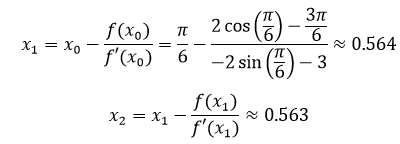
第二次迭代与第一次迭代的差距已经非常微小,可以说x2就是最终的近似解。
求平方根
在一次code review会议上,一个同事展示了一段他不理解的C++代码:
1 const float EPS = 0.00001; 2 3 doublesqrt(doublex){ 4 if(x == 0) 5 return 0; 6 7 double result = x; 8 double lastValue; 9 do{ 10 lastValue = result; 11 result = result/2.0f + x/2.0f/result; 12 }while(abs(result - lastValue) > EPS); 13 14 return result; 15 }
sqrt函数是求平方根,并且运行的很好,虽然展示者能够看懂每一行代码,但不知道为什么要这么写,不明白那个神奇的2.0是什么意思。
现在看起来,不懂数学都没法快乐地阅读代码了。这段代码其实是在使用牛顿法计算平方根,过程是这样的:
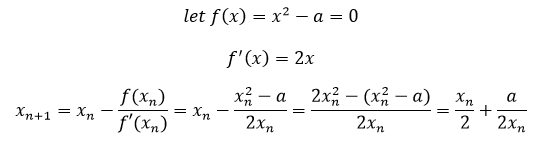
如果改成计算机程序的写法:
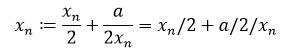
现在可以和第9行代码对应上了。
作者:我是8位的




 浙公网安备 33010602011771号
浙公网安备 33010602011771号