线性代数笔记17——正交向量与正交子空间
正交向量
正交是垂直的令一种说法，两个向量正交意味着两个向量的夹角是90°。
这可以用直角三角形的三边解释：
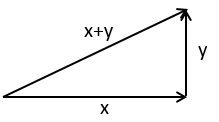
当x和y正交时，二者的点积是0，反过来也一样。这个结论在n维空间也适用，当Rn空间内的两个向量x和向量y正交时：
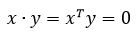
如果x是零向量，xTy还是0，也意味着零向量和任意向量正交。
正交子空间
正交性还可以推广到子空间，如果说一个子空间V和另一个子空间W正交，那么V中的每一个向量和W中的每一个向量正交。
子空间V的正交子空间W也称为V的正交补空间，或V的正交补，记作：
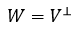
正交与垂直
以我们比较熟悉的三维空间为例，墙角就可以看作一个典型的空间坐标系，两个墙面和地面两两垂直，每个平面都是三维空间中的二维子空间，这是否意味着子空间的正交呢？并不是这样，两个平面垂直并不等同于两个子空间正交，可以轻易找出两个分属于两个平面但不垂直的向量。实际上，在墙壁与地面的交接处，沿着接缝方向的向量同属于两个平面，但它们不会自己正交与自己，除非是零向量。
这样看来，“正交是垂直的令一种说法”并不完全准确，实际上，正交一定垂直，垂直不一定正交。
通过平面的例子可以看出，如果两个子空间交于一个非零向量，那么这两个子空间一定不会正交。换句话说，如果两个子空间正交，它们只能交于零向量（单独的点就是零向量，它没有方向，或者说有任意方向，并且模长为0）。
在同一个平面中正交的例子有哪些呢？
回顾一下子空间的定义，如果V是Rn的线性子空间，则V一定满足三个条件：
- 包含0向量；
- x是V中的一个向量，x和一个标量的乘积也在V中，即数乘封闭性；
- a和b是V中的向量，a+b也在V中，即加法封闭性。
由此可见平面内只有三个子空间：原点、过原点的直线、整个平面。这样一来答案就很清晰了：
- 过原点的直线任何时候都不会和整个平面正交；
- 原点和所有过原点的直线正交，也和整个平面正交；
- 如果两个过原点的向量的点积是0，二者正交。
四个基本子空间的正交补
先看行空间如何正交与零空间。零空间的意义是Ax = 0时x的解集：
这样会发现，A中的每个行向量都正交于零空间中的x：
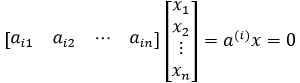
a(i)表示A中的第i行行向量，a(i)x = 0当于一个向量垂直于一个超平面。当然，行空间不仅仅包括这几行，还包括它们的线性组合，只要证明满足加法和数乘封闭性即可：
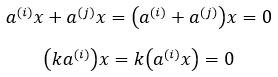
列空间相当于A转置后的行空间，道理是一样的，所以列空间也正和零空间正交。
A是m×n矩阵，四个基本子空间的正交性可以用下图表示，其中r是矩阵的秩：
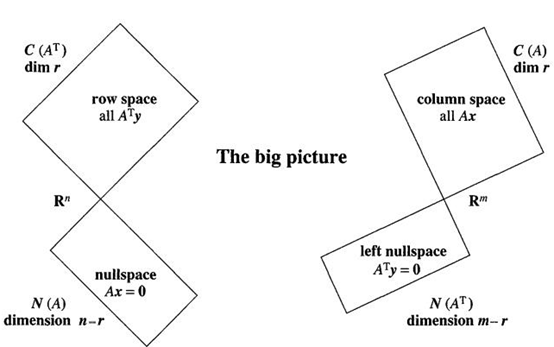
这相当于把m维空间分割成两个子空间，n维空间分割成另两个子空间，子空间的维数满足图中的要求。如果用正交补的记法，上图可以看作：
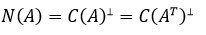
以三维空间中为例：
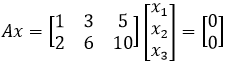
A的行向量是线性相关的，A的秩是1，所以行空间是1维的，是一条直线，与之正交的零空间是垂直于行向量的平面，<1, 3, 5>就是这个平面的法向量，由此可以得到平面方程：
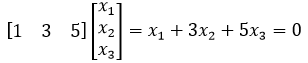
作者：我是8位的
