线性代数笔记14——行空间和左零空间
前面已经介绍了矩阵的零空间和列空间，它们都属于矩阵的四个基本子空间，基本子空间还包括行空间和左零空间。
召唤一个矩阵：
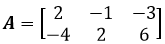
为了找出零空间和列空间，先进行套路运算——转换为行最简阶梯矩阵：
只有一个主元，也就是仅有一个向量都是独立向量，列空间是：
这同时也意味着矩阵A的秩是1。矩阵的秩、列空间的基的向量数、独立向量数、主元数，这些都是一个意思，只是用于不同场景中，这些概念往往容易让人混淆。实际上直到今天，我仍然会对一些概念产生一瞬间或几分钟的困惑，不得不重新翻阅资料。
再来看零空间，主元可以用另外两个自由元表示，这里用x2和x3表示x1：
A的零空间：
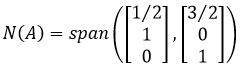
左零空间
零空间关注的是Ax = 0的解，除此之外，我们还想关注转置后的A形成的方程的性质，也就是ATx = 0的解。还是刚才的矩阵，看看A转置后的零空间：
套路运算，行最简阶梯型矩阵：
第二列可以用第一列表示，第二列是第一列的线性组合，只有一个独立向量，只有一个主元，秩是1……一大堆相似概念，最终可以得到这样的方程：
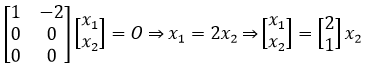
AT的零空间：
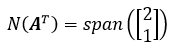
独立地看，AT的零空间是ATx = O的解，这又有什么用呢？它与Ax = O有什么关系？
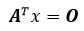
如果把等式两边同时转置，右侧依然是趴下的零向量，左侧：
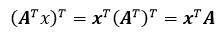
这下清晰了，A的零空间是将A右乘x；如果左乘x就是AT的零空间：
由于x在A的左侧，所以AT的零空间也叫A的左零空间。
行空间
A的行空间也就是AT的列空间，A的秩是在回答A中有多少列是线性无关的，AT是在回答A中有多少行是线性无关的。有趣的是，A的秩和AT的秩相等。理解这里一点很有用，尤其是在确定列空间的基时，辅助行空间可以帮助我们避免一些陷阱，比如下面这个矩阵：
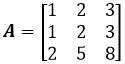
三列是否是线性无关的？如果最有一个列向量是<3, 3, 7>，那么很明显第三个向量可以由前两个向量代替，现在第三个向量稍稍偏移了一点，所以三个向量应该是线性无关的。真是这样吗？
实际上我们不必去计算，A的列向量之间的关系没那么明显，但是行向量则不然——前两个行向量相同，A中只有两个线性无关的行向量，也就是A的秩是2，所以A的列向量也不是独立向量。
空间和维数
前面已经多次出现过维度的概念，如果有一个Am×n矩阵，它的四个基本子空间的维数各是多少呢？
只要清楚四个基本子空间的概念，这个问题就比较容易回答。列空间的一组基一定包含A的一个列向量，这个列向量是m维的，所以列空间一定在Rm中；同理，行空间在Rn中。具体来说，由于秩是r，所以列空间是Rm中的r维子空间，行空间是Rn中的r维子空间。
零空间是Ax = 0中x的解，x是n维向量，所以零空间在Rn中；同理，左零空间在Rm中。零空间的维数是由自由元决定的，自由元等于矩阵列数减去主元个数，也就是n – r，所以零空间是n维空间内的n – r维子空间。左零空间是m维空间内的m – r维子空间。
总结一下：
列空间，位于Rm下的r维空间
行空间，位于Rn下的r维空间
零空间，位于Rn下的 n – r维空间
左零空间，位于Rm下的 m – r维子空间
行空间的基
可以先对矩阵转置，在通过列空间的方式寻找行空间的基。这样做没错，但多少有些无聊，我们更希望一次就能同时找到列空间和行空间的基。看个例子：
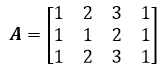
A的列空间和行空间都比较容易确定，甚至不需要化简：
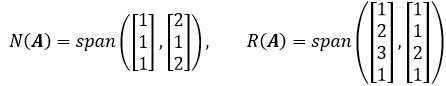
虽然列空间和行空间的独立向量个数相等，但列空间和行空间可不行等，所以还是需要某种通用的方法。仍然是先将A化简为行最简阶梯形矩阵：
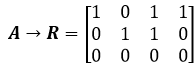
R是A的行最简阶梯矩阵，通过R可以确认A的秩r = 2。下面是关键：对于A来说，行空间的基是R的前r行，即：
之所以能够得到这样的结论，是因为从A到R的变换本来就是通过行的线性变换得到的，变换到最后，R中只留下了线性无关的行向量。这实际是在说，R是最简行阶梯矩阵，R中的每一级阶梯都是线性无关的。
左零空间的基
召唤一个矩阵：
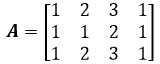
直接的方法是使用左零空间的定义，将A转置，然后求解AT的零空间：
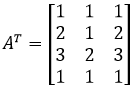
这和求解零空间一样，化简为行最简阶梯形矩阵：
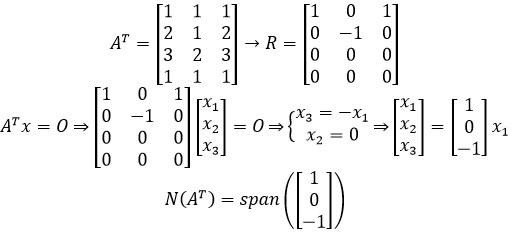
这就是A的左零空间。这样计算简单粗暴。
另外一种方法是使用高斯-诺当消元法，通过记录行变换的方式找到左零空间。这种方法的大概思路是和求逆矩阵类似，其过程是使[Am×n Im×m]→[Rm×n Em×m]，如果A是方阵，R是单位矩阵，则转化过程和求逆一致。
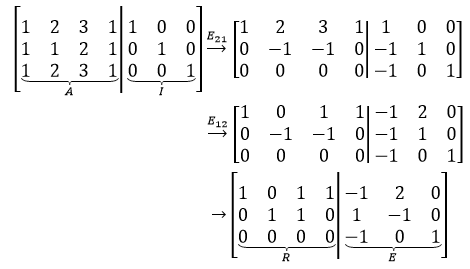
E实际上是记录了从A到R的初等行变换，EA = R。如果用《线性代数9——消元矩阵与置换矩阵》中的方法写出来，其过程如下：
最终的消元矩阵：
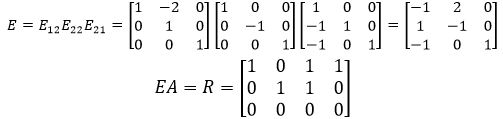
费了很大劲求出E，目的是为了得到A的左零空间，R的最后一行是OT，也就是说E的最后一行与A的乘积是OT：
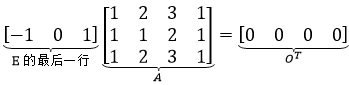
这相当于：
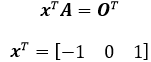
现在可以确定，A的左零空间是：
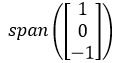
这个方法的思路是寻找一个零行向量OT的行组合。
作者：我是8位的
