线性代数笔记9——消元矩阵与置换矩阵
消元矩阵
如果用矩阵表示一个有解的方程组，那么矩阵经过消元后，最终能变成一个上三角矩阵U。用一个三元一次方程组举例：
A经过一些列变换，最终得到了一个上三角矩阵U：
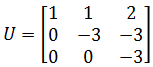
回代到方程组后可以直接求解：
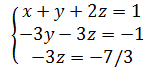
如果上面的变换去掉增广矩阵，可以简写为：
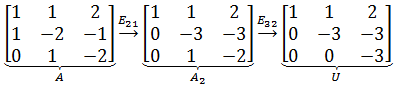
矩阵的初等变换可以用矩阵乘法实现，现在的问题是，我们能否得到一个可以表示整个消元过程的矩阵E，使得E与A相乘能够直接得到U？还是以上面的矩阵为例，第一次变换是用第二行加上第一行的-1倍，所以只需将A的左边乘以E21就可以：
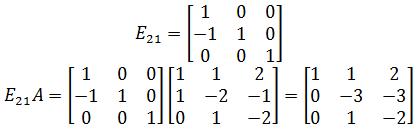
这里的矩阵E21又是怎么来的呢？这需要回归一下消元的过程：
首先，A的第一行不变，因此我们需要拿出A的1个第一行，0个第二行，0个第三行，于是(1 ,0, 0)组成了E21的第一行；
然后，我们需要-1个A的第一行，1个第二行，0个第三行进行线性组合，所以(-1, 1, 0)组成了E21的第二行；
最后，因为A的第三行不变，因此需要0个第一行，0个第二行，1个第三行，所以E21的第三行是(0, 0, 1)。
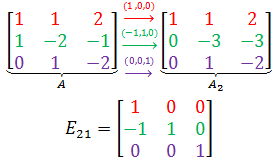
经过变换，得到了A2，可以用E21A = A2表示。A2继续变换：
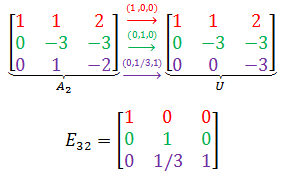
最终，E32(E21A ) = (E32E21)A = U，E = E32E21
置换矩阵
同样可以使用矩阵相乘来完成行交换和列交换。
首先是行交换，对矩阵进行如下变换：
对于A2的第一行，相当于从A中拿出了0个第一行，1个第二行，0个第三行；
对于A2的第二行，相当于从A中拿出了1个第一行，0个第二行，0个第三行；
对于A2的第三行，相当于从A中拿出了0个第一行，0个第二行，1个第三行。
上面的P12称为行置换矩阵。可以看出置换矩阵是一个每行只有一个维度是1的满秩矩阵，或者说是行重新排列了的单位矩阵，它的一个特性是 P-1 = PT
行交换与行交换类似，但是需要将左乘变为右乘。
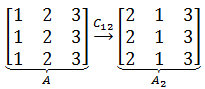
对于A2的第一列，相当于从A中拿出了0个第一列，1个第二列，0个第三列；
对于A2的第二列，相当于从A中拿出了1个第一列，0个第二列，0个第三列；
对于A2的第三列，相当于从A中拿出了0个第一列，0个第二列，1个第三列。
C12称为列置换矩阵。注意列置换矩阵的结果，是按照列构成的。
作者：我是8位的
