寻找“最好”(5)——无解之解
我所在的城市里,市中心有一座邮政大楼,小时候,那可是全市最高建筑!每到整点,楼顶的大钟就奏起《松花江上》,即使相隔很远也能听见。当时我对大楼的高度充满好奇,经常想着怎样用格尺去测量。初中学了方程组和几何后,我想到一种有效的方案,终于可以用格尺测量。
测量方法大概是这样:找到一根木棍插在地上,在视线中,当木棍顶端正好遮住楼顶时,记录下我所处位置与木棍的距离x1,再用另一根木棍用同样的方法记下另一个距离x2,如下图所示:
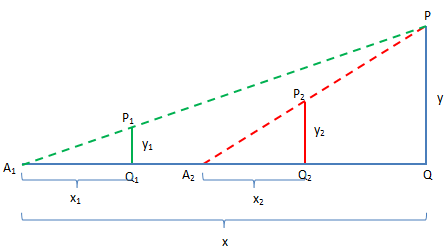
A1和A2是我两次测量时所处的位置,y1和y2是两根木棍的高度,因为测量时我是趴在地上,所以假设我的观察点和地面的距离是0;又因为我在测量时距离大楼很远,所以A1Q和A2Q的长度未知。通过这种方式可以建立一个方程组,设A1Q = x:
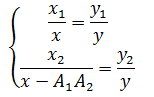
两个方程,两个未知数,有唯一解,这下可以知道邮政大楼的高度了!
无解的方程
过了几天,我又去测量了一次,因为重新找了两根木棍,所以得到的数据略有区别。然而奇怪的是,这次得到的y值和原来相差很大。第一个感觉是量错了,所以进行了第三次测量,得到了第三组的近似数据,也得到了误差很大的新y值。测量继续进行……
|
测量次数 |
A1Q1 |
A2Q2 |
P1Q1 |
P2Q2 |
A1A2 |
|
1 |
X1(1) |
X2(1) |
y1(1) |
y2(1) |
a(1) |
|
2 |
X1(2) |
X2(2) |
y1(2) |
y2(2) |
a(2) |
|
3 |
X1(3) |
X2(3) |
y1(3) |
y2(3) |
a(3) |
|
… |
… |
… |
… |
… |
… |
|
10 |
X1(10) |
X2(10) |
y1(10) |
y2(10) |
a(10) |
因为工具粗糙,并且视角略有差别,每一组的数据都不同。这下有意思了,20个方程,2个未知数,其中任意两个方程都唯一解,任意三个方程都无解:
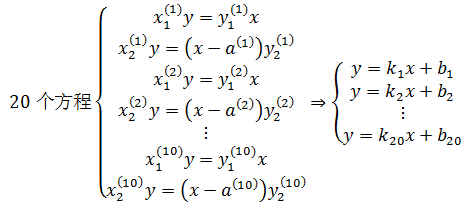
在当时,这个变态的方程组已经远远超出我的理解范围,所以我得出结论——数学没有实用性。
约等方程组
大学学习了微积分,我第一次体会到数学的神奇;后来研究机器学习,更体会到数学的重要性。终于有一天,我想起了家乡的邮政大楼。
问题的关键是,测量存在误差,这就导致等式方程实际上是约等:
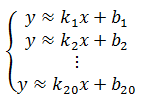
大多是时候,数学的推理是基于全等,我们可以通过a = b, b = c推出a = c,这在约等中是否成立呢?举一个实际的例子,向一个容积是1升的水杯中倒水,第一次差100毫升倒满,第二次溢出100毫升。从结果看,两次都和满水状态相差100毫升,但是两者之间却相差200毫升。从状态看,一次是“亏损”,一次是“盈余”,截然相反,让二者约等更不合逻辑了。如果用数字举例,四舍五入,1.4≈1;1.4≈1.45,1.45≈1.5,1.5≈2,最后的结论是1≈2,如果这都可以,那么根据该逻辑,可以推出1约等于任意数。
无解之解
现在看来,约等方程组不能按照解等式方程组的方法求解了,但是可以寻找到一组x和y(k和b已知),使得所有方程的左右两边都尽最大可能相等,这在机器学习中就是常见的数据拟合了。思路大概是这样的,既然每个测量都存在误差,那么每个y的真实值实际上是计算值加误差:
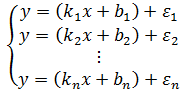
这里ε是误差。现在,需要寻找x和y,使得所有方程中的ε最小,这相当于方程组的总误差最小:
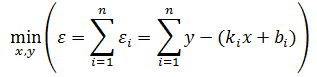
因为ε有正有负,取绝对值又变成了非凸优化,所以将各项取平方:
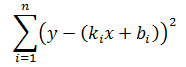
这就是平方和损失函数了,可以通过令x和y的偏导等于0,转换成关于x和y的二元一次方程组,最终求得唯一解。关于最小二乘法,可参考《多变量微积分笔记2——最小二乘法》。
作者:我是8位的




 浙公网安备 33010602011771号
浙公网安备 33010602011771号