线性代数笔记8——求解逆矩阵

　　在第一章中介绍了逆矩阵与奇异矩阵，我们可以通过一个行列式公式计算二维矩阵的逆，那么更多维矩阵的逆如何求解呢？

逆矩阵与方程组

　　或许用行列式求逆矩阵的做法有些公式化，实际上可以将求逆矩阵看成解方程组：

 

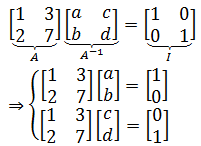
　　由此可以通过解方程组的方式求出逆矩阵。

　　如果一个方阵与另一个非零矩阵的乘积是零矩阵，那么该矩阵是奇异矩阵，也是就是没有逆。例如：

 

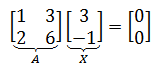
　　因为AX = 0，A是奇异矩阵，如果A可逆，则有：

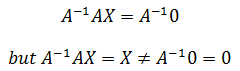
高斯-诺当消元法

　　解方程组的方式虽然直观，但有些麻烦，可以用高斯-诺尔当(Gauss-Jordan)方法通过消元去求逆矩阵：

　　可以看到，高斯-诺尔当消元法的原理是AI 通过初等变换，最终得到 IA^-1

　　示例

　示例中经历了四次初等变换，把第i行第j列的消元记作E_ij，即消元后，第i行第j列的元素为0；第i行和第j行互换记作S_ij，则从A到A^-1的变换过程是：E₃₁→E₂₂→E₁₃→S₂₃，写在一起：S₂₃E₁₃E₂₂E₃₁：

　　可以看到，高斯-诺当消元法最终使得 (S₂₃E₁₃E₂₂E₃₁)A = A^-1A = I

逆矩阵与方程组

　　 可以将一个方程组转换为矩阵相乘：

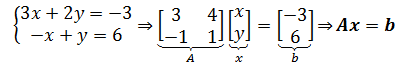
　　上式最终变成了向量相乘，这就和普通的代数类似，两边同时乘以A^-1：

 

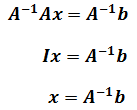
　　现在，可以通过求A^-1，然后使用普通的矩阵乘法求解方程组，最终解得x=-3,y=3。

逆矩阵的基础公式

相乘矩阵的逆

　　假设A和B都可逆，那么：

 

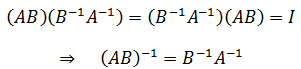
转置矩阵的逆

　　如果A是可逆矩阵，那么A^T的逆是什么？

　　将A^-1A = I左右两侧同时转置：

 

 

 

 

---

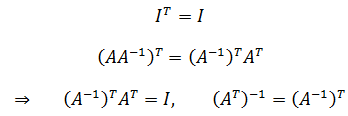
　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”